前言
在数据科学、工程优化和其他科学计算领域中,向量和矩阵的运算是核心组成部分。MAPL作为一种数学规划语言,为这些领域的专业人员提供了强大的工具,通过向量式和矩阵式变量声明以及丰富的内置数学运算支持,大大简化了数学建模和优化问题的处理。在本文中,我们将探索MAPL的这些特性,并且通过示例来展示如何有效使用这些工具。
介绍与应用
矩阵和向量变量声明
在MAPL中,向量和矩阵变量的声明非常直观。例如,使用var X(3,2)可以创建一个3行2列的矩阵,而使用var Y(3)会创建一个包含3个元素的列向量。对这些变量的操作,如索引(X[1,0])和赋予初值,都可以使用易于理解的语法来完成。
var X(3,2) >=0 integer;print "Structure of X is:";
print X;print "----------------";
print "Sample Entries:";
print X[0,0];
print X[1,1];
print X[2,1];
结果如下:
Structure of X is:
[[ X0, X1],[ X2, X3],[ X4, X5]]
----------------
Sample Entries:
+ [0, 0] -> integer [LB, UB, SOLN-VAl] = [0.000000, +inf, 0.000000
+ [1, 1] -> integer [LB, UB, SOLN-VAl] = [0.000000, +inf, 0.000000]
+ [2, 1] -> integer [LB, UB, SOLN-VAl] = [0.000000, +inf, 0.000000]
张量运算支持
张量运算是MAPL中一项强大的特性,它允许我们使用类似于线性代数中的标准操作符,例如:
- 加法和减法(+,-):逐元素进行操作,要求操作数尺寸相同。
- 乘法(*):支持标量和矩阵的乘法,以及矩阵与向量之间的乘法,必须满足传统的行列匹配规则。
- 转置('):快速提供变量的转置形式,仅适用于矩阵。
- 点乘(.*):逐元素乘法,用于两个相同尺寸的矩阵或向量。| 类型 | 操作符 | 说明 | 是否支持标量 | 用例 |
| ---------- | ------ | ------------------------- | ------------ | ----------------- |
| 一元操作符 |+| 向量/矩阵加法 | 是 |X+Y|
| |-| 向量/矩阵减法,或者求反 | 是 |X-Yor-X|
| |.*| 逐元素乘法 | 否 |X.*Y|
| |*| 向量/矩阵乘法 | 是 |X*Y|
| |'| 矩阵转置 | 否 |X'|
| |/| 向量/矩阵逐元素除以某标量 | 是 |X/2|
| 二元操作符 |^| 逐元素的p次幂 | 是 |X^2|
| 索引操作符 |[]| 获取指定位置的值 | 否 |X[3], Y[3,5]|
这些运算符为建模提供了极大的灵活性和表现力,支持以直观和自然的方式表达数学关系。
映射函数
映射函数是处理张量式变量必不可少的一部分,使建模张量间的函数变换更方便。MAPL提供了一系列映射函数,如exp、log和sin等,它们可以逐元素应用于向量或矩阵。例如,对于一个矩阵A,exp(A)会计算A中每个元素的指数值。
clear model;
var x(3,2) >=0;A = exp(x);print A;
运行上述代码,结果如下:
[[e^(x0), e^(x1)],[e^(x2), e^(x3)],[e^(x4), e^(x5)]]
混合计算和表达式引用
MAPL不仅支持张量间的运算,还支持张量和标量之间的混合计算。此外,它允许用户为复杂的表达式命名,以便于后续引用,这样可以避免重复的计算,并使模型清晰易于管理。
var x >=0;
var y(3,4);A = x + y;
B = y + x;
C = x - y;
D = y - x;
E = -y;
F = x*y;print y;
print A;
print B;
print C;
print D;
print E;
print F;
输出如下:
[[ y0, y1, y2, y3],[ y4, y5, y6, y7],[ y8, y9, y10, y11]][[ x+y0, x+y1, x+y2, x+y3],[ x+y4, x+y5, x+y6, x+y7],[ x+y8, x+y9, x+y10, x+y11]][[ y0+x, y1+x, y2+x, y3+x],[ y4+x, y5+x, y6+x, y7+x],[ y8+x, y9+x, y10+x, y11+x]][[ x-y0, x-y1, x-y2, x-y3],[ x-y4, x-y5, x-y6, x-y7],[ x-y8, x-y9, x-y10, x-y11]][[ y0-x, y1-x, y2-x, y3-x],[ y4-x, y5-x, y6-x, y7-x],[ y8-x, y9-x, y10-x, y11-x]][[ -y0, -y1, -y2, -y3],[ -y4, -y5, -y6, -y7],[ -y8, -y9, -y10, -y11]][[ x*y0, x*y1, x*y2, x*y3],[ x*y4, x*y5, x*y6, x*y7],[ x*y8, x*y9, x*y10, x*y11]]一个完整示例
带资源上限约束的二分匹配问题(也称为加权二分匹配问题或指派问题)是图论中的一个经典问题,它的目的是在二分图中找到最优的匹配,使得匹配的总权重最大,同时不超过给定的资源上限。
线性数学建模如下:
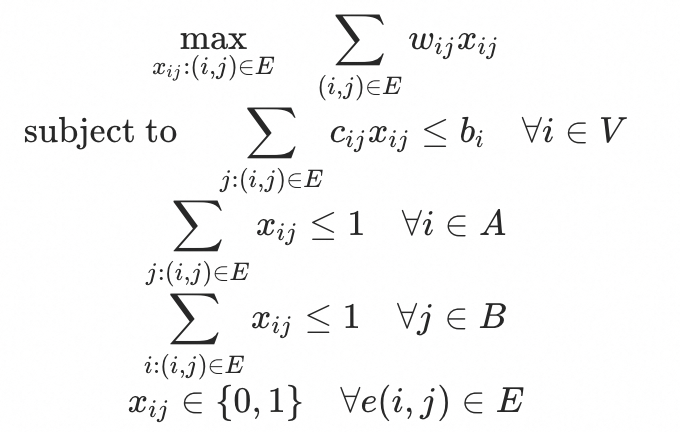
向量形式:
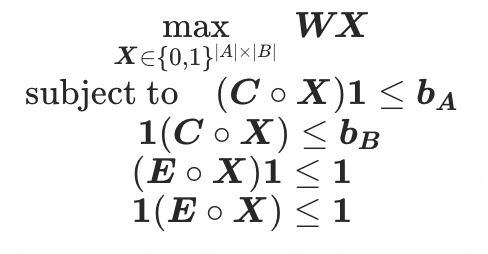
代码建模如下,可复制在云上平台直接运行:
########################################
#
# 向量式建模案例
# Weighted Bipartite Matching
#
######################################### 1.读取权重及损耗矩阵
param W = read_csv("weight.data");
param C = read_csv("cost.data");param m = W.row;
param n = W.col;############## 2.问题建模 ###############
# 定义矩阵形式变量X,表示可行的匹配
var X(m, n) binary; # 3.二分匹配问题建模
maximize sum(W.*X);# A集合的资源上限约束
s.t. (C.*X)*ones(n,1) <= 10;
# B集合的资源上限约束
s.t. ones(1,m)*(C.*X) <= 10;# 集合A中每个节点最多匹配一次
s.t. X * ones(n, 1) <= 1;
# 集合B中每个节点最多匹配一次
s.t. ones(1, m) * X <= 1;############## 问题求解 #################
# 3.调用mindopt求解
option solver mindopt;
solve;############## 结果分析 #################
# 输出最优目标函数值
param obj = sum(W.*X);
print "Optimal obj is: {:.2f}" % obj;# 输出最优匹配
print "Optimal X is";
print X;
#######################################
输出结果如下:
Running mindoptampl
wantsol=1
MindOpt Version 1.0.1 (Build date: 20231114)
Copyright (c) 2020-2023 Alibaba Cloud.Start license validation (current time : 05-FEB-2024 10:34:07).
License validation terminated. Time : 0.008sModel summary.- Num. variables : 50- Num. constraints : 30- Num. nonzeros : 200- Num. integer vars. : 50- Bound range : [1.0e+00,1.0e+01]- Objective range : [4.0e-01,9.8e+00]Branch-and-cut method started.
Original model: nrow = 30 ncol = 50 nnz = 200
Tolerance: primal = 1e-06 int = 1e-06 mipgap = 0.0001 mipgapAbs = 1e-06
Limit: time = 1.79769313486232e+308 node = -1 stalling = -1 solution = -1
presolver terminated; took 1 ms
presolver terminated; took 3 ms
Parallelism: root=8, tree=10accept new sol: obj 0 bnd vio 0 int vio 0 mipgap inf time 0accept new sol: obj -42.8999996185303 bnd vio 0 int vio 0 mipgap 4.55011660905533 time 0
Model summary.- Num. variables : 48- Num. constraints : 15- Num. nonzeros : 96- Bound range : [1.0e+00,1.0e+00]- Objective range : [4.0e-01,9.8e+00]- Matrix range : [1.0e+00,1.0e+00]Presolver started.
Presolver terminated. Time : 0.002sSimplex method started.
Model fingerprint: ==gZ3Fmb392Y3JmZIteration Objective Dual Inf. Primal Inf. Time0 -2.38100e+02 0.0000e+00 8.1000e+01 0.03s 6 -4.29000e+01 0.0000e+00 0.0000e+00 0.03s
Postsolver started.
Simplex method terminated. Time : 0.007sRoot relaxation: -42.8999996185303 iteration = 6 time = 0.03
Branch-and-cut method terminated. Time : 0.548sOPTIMAL; objective 42.90Completed.Optimal obj is: 42.90
Optimal Matching X is
[[0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 1, 0, 0, 0, 0],[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 1, 0, 0]]
完整案例介绍:案例1:加权二分匹配(Weighted Bipartite Matching)
详细语法:向量化建模
结论:
MAPL作为一种先进的建模语言,通过支持向量和矩阵的声明以及丰富的运算操作符和映射函数,为用户处理多维数据提供了强大的工具集。无论是在学术研究还是工业应用中,MAPL的这些特点都显著地提高了数学建模的效率和便捷性。