问题一：移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2
, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,3,0,4]
解释：函数应该返回新的长度为5，前五个元素为0，1，3，0，4
。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

那这个问题我们该如何来思考呢？

这个题我们可以定义两个指针变量，用dst来遍历整个数组，例如：

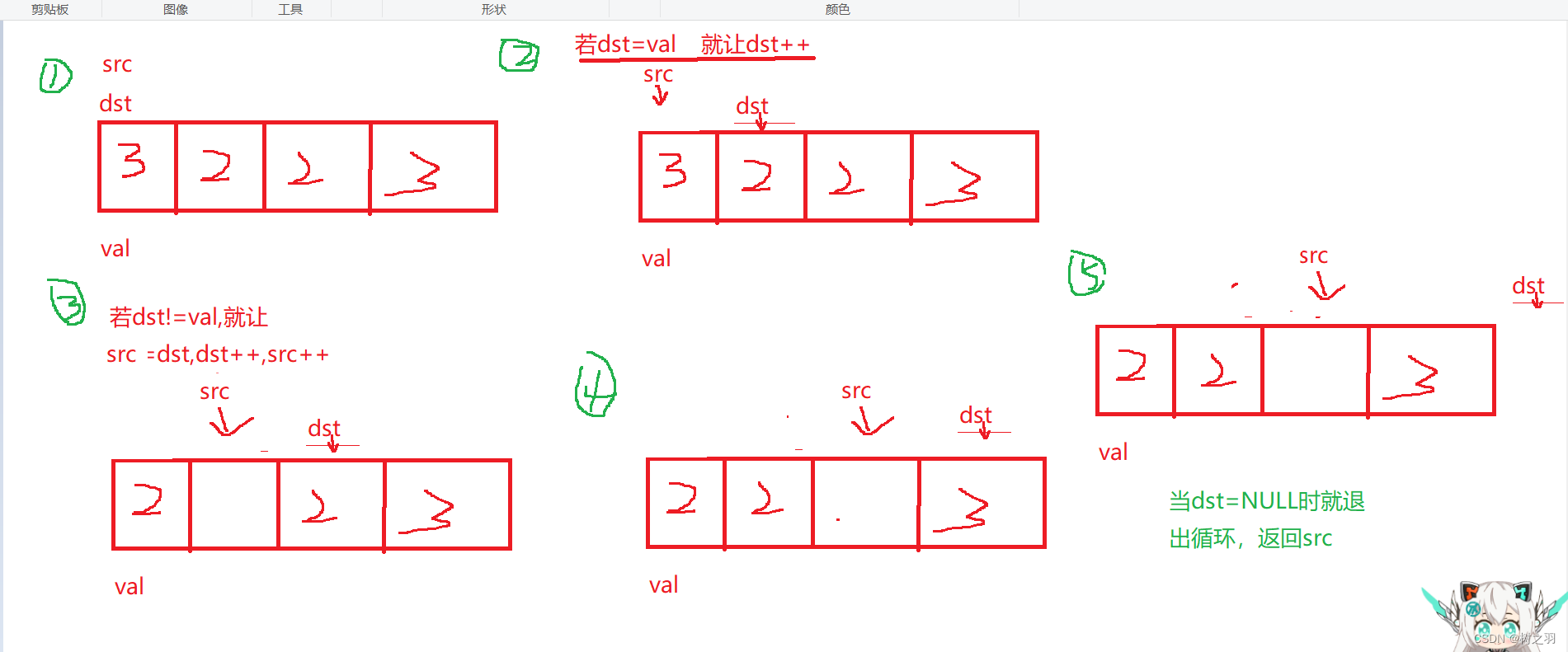
 接下来我们进行代码实现

int removeElement(int* nums, int numsSize, int val) {int src, dst;src = dst = 0;while (src < numsSize){if (nums[src] == val){src++;}else{nums[dst] = nums[src];src++;dst++;}}return dst;
}int main()
{int nums[] = { 3,2,2,3 };int numsSize = sizeof(nums)/sizeof(nums[0]);int len=removeElement(nums, numsSize,3);for (int i = 0; i < len; i++){printf("%d ", nums[i]);}return 0;
}

总结：这个题主要是让我们在不创建新数组的情况下删除与val相同的数，这时我们就可以通过画图进行分析，创建两个指针我们就能很好的解决问题。

问题二：合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

 这个题我们该怎么思考呢？本题我们依然采用先画图来分析

 通过以上分析我们大概知道了思路我们接下来进行代码实现：

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {int l1 = m - 1;int l2 = n - 1;int l3 = m + n - 1;while (l1 >= 0 && l2 >= 0){if (nums1[l1] < nums2[l2]){nums1[l3--] = nums2[l2--];}else{nums1[l3--] = nums1[l1--];}}while (l2 >= 0){nums1[l3--] = nums2[l2--];}}

总结：这个两个体都是与数据结构中的顺序表相关的问题，当我们无法想出答案是我们可以进行画图能使我们很快的解决问题。