目录
线性激活函数的导数
Softmax激活函数的导数
S型激活函数的导数
双曲正切激活函数的导数
ReLU激活函数的导数
如何在反向传播中应用
批量训练和在线训练
随机梯度下降
反向传播权重更新
选择学习率和动量
Nesterov动量
政安晨的个人主页:政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: 政安晨的机器学习笔记
希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正!
反向传播过程需要激活函数的导数,它们通常确定反向传播过程将如何执行。大多数现代深度神经网络都使用线性、Softmax和ReLU激活函数。我们还会探讨S型和双曲正切激活函数的导数,以便理解ReLU激活函数为何表现如此出色。
线性激活函数的导数
线性激活函数被认为不是激活函数,因为它只是返回给定的任何值。因此,线性激活函数有时称为一致激活函数。该激活函数的导数为1,如下公式所示:
![]()
如前文所述,希腊字母表示激活函数,在
右上方的撇号表示我们正在使用激活函数的导数。这是导数的几种数学表示形式之一。
Softmax激活函数的导数
在本文中,Softmax激活函数和线性激活函数仅在神经网络的输出层上使用。
方便起见,下面公式再次展示了Softmax激活函数:
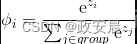
z向量代表所有输出神经元的输出。
下面公式展示了该激活函数的导数:
![]()
对于上述导数,我们使用了稍微不同的符号。带有草书风格的∂符号的比率表示偏导数,当你对具有多个变量的方程进行微分时会使用这个符号。要取偏导数,可以将方程对一个变量微分,而将所有其他变量保持不变。上部的∂指出要微分的函数。在这个例子中,要微分的函数是激活函数。下部的∂表示偏导数的分别微分。在这个例子中,我们正在计算神经元的输出,所有其他变量均视为常量。
微分是瞬时变化率:一次只有一个变量能变化。
如果使用交叉熵误差函数,就不会使用线性或Softmax激活函数的导数来计算神经网络的梯度。
通常你只在神经网络的输出层使用线性和Softmax激活函数。
因此,我们无须担心它们对于内部节点的导数。
对于使用交叉熵误差函数的输出节点,线性和Softmax激活函数的导数始终为1。
因此,你几乎不会对内部节点使用线性或Softmax激活函数的导数。
S型激活函数的导数
下面公式展示了S型激活函数的导数:
![]()
机器学习经常利用公式上面中表示的S型激活函数。我们通过对S型函数的导数进行代数运算来导出该公式,以便在其自身的导数计算中使用S型激活函数。为了提高计算效率,上述激活函数中的希腊字母表示S型激活函数。
在前馈过程中,我们计算了S型激活函数的值。保留S型激活函数的值使S型激活函数的导数易于计算。
双曲正切激活函数的导数
下面公式给出了双曲正切激活函数的导数:
![]()
在咱们这个系列文章中,我们建议使用双曲正切激活函数,而不是S型激活函数。
ReLU激活函数的导数
下面公式展示了ReLU激活函数的导数:

严格来说,ReLU激活函数在0处没有导数,但是,由于约定,当x为0时,0处的梯度被替换。具有S型和双曲正切激活函数的深层神经网络可能难以通过反向传播进行训练。造成这一困难的因素很多,梯度消失问题是最常见的原因之一。
下图展示了双曲正切激活函数及其梯度/导数。

上图表明,当双曲正切激活函数(实线)接近−1和1时,双曲正切激活(虚线)的导数消失为0。
S型和双曲正切激活函数都有这个问题,但ReLU激活函数没有。
下图展示了S型激活函数及其消失的导数:

如何在反向传播中应用
反向传播是一种简单的训练算法,可以利用计算出的梯度来调整神经网络的权重。该方法是梯度下降的一种形式,因为我们将梯度降到较低的值。随着程序调整这些权重,神经网络将产生更理想的输出。神经网络的整体误差应随着训练而下降。在探讨反向传播权重的更新过程之前,我们必须先探讨更新权重的两种不同方式。
批量训练和在线训练
我们已经展示了如何为单个训练集元素计算梯度。在本文的前面,我们对神经网络输入[1,0]并期望输出1的情况计算了梯度。对于单个训练集元素,这个结果是可以接受的,但是,大多数训练集都有很多元素。因此,我们可以通过两种方式来处理多个训练集元素,即在线训练和批量训练。
在线训练意味着你需要在每个训练集元素之后修改权重。利用在第一个训练集元素中获得的梯度,你可以计算权重并对它们进行更改。训练进行到下一个训练集元素时,也会计算并更新神经网络。训练将继续进行,直到你用完每个训练集元素为止。至此,训练的一个迭代或一轮(epoch)已经完成。
批量训练也利用了所有训练集元素,但是,我们不着急更新所有权重。作为替代,我们对每个训练集元素的梯度求和。一旦我们完成了对训练集元素梯度的求和,就可以更新神经网络权重。至此,迭代完成。
有时,我们可以设置批量的大小。
如你的训练集可能有10 000个元素,此时可选择每1 000个元素更新一次神经网络的权重,从而使神经网络权重在训练迭代期间更新10次。
随机梯度下降
批量训练和在线训练不是反向传播的仅有选择。
随机梯度下降(SGD)是反向传播算法中最受欢迎的算法。
SGD可以用批量或在线训练模式工作。在线SGD简单地随机选择训练集元素,然后计算梯度并执行权重更新。该过程一直持续到误差达到可接受的水平为止。与每次迭代遍历整个训练集相比,选择随机训练集元素通常会更快收敛到可接受的权重。
批量SGD可通过选择批量大小来实现。
对于每次迭代,随机选择数量不应超过所选批量大小的训练集元素,因此选择小批量。更新时像常规反向传播批量处理更新一样,将小批量处理中的梯度相加。这种更新与常规批量处理更新非常相似,不同之处在于,每次需要批量时都会随机选择小批量。迭代通常以SGD处理单个批量。批量大小通常比整个训练集小得多。批量大小的常见选择是600。
反向传播权重更新
现在,我们准备更新权重。如前所述,我们将权重和梯度视为一维数组。给定这两个数组,我们准备为反向传播训练的迭代计算权重更新。下面公式给出了为反向传播更新权重的公式:
![]()
上面公式计算权重数组中每个元素的权重变化。你也会注意到,上面公式要求对来自上一次迭代的权重进行改变。你必须将这些值保存在另一个数组中。如前所述,权重更新的方向与梯度的符号相反:正梯度会导致权重减小,反之负梯度会导致权重增大。由于这种相反关系,上面公式以负号开始。
上面公式将权重增量计算为梯度与学习率(以ε表示)的乘积。
此外,我们将之前的权重变化与动量值(以α表示)的乘积相加。
学习率和动量是我们必须提供给反向传播算法的两个参数。选择学习率和动量的值对训练的表现非常重要。不幸的是,确定学习率和动量主要是通过反复试验实现的。
学习率对梯度进行缩放,可能减慢或加快学习速度。低于1.0的学习率会减慢学习速度。如学习率为0.5会使每个梯度减少50%;高于1.0的学习率将加速训练。实际上,学习率几乎总是低于1。
选择过高的学习率会导致你的神经网络无法收敛,并且会产生较高的全局误差,而不会收敛到较低值。
选择过低的学习率将导致神经网络花费大量时间实现收敛。
和学习率一样,动量也是一个缩放因子。
尽管是可选的,但动量确定了上一次迭代的权重变化中有百分之多少应该应用于这次迭代。如果你不想使用动量,只需将它的值指定为0。
动量是用于反向传播的一项技术,可帮助训练逃避局部最小值,这些最小值是误差图上的低点所标识的值,而不是真正的全局最小值。反向传播倾向于找到局部最小值,而不能再次跳出来。这个过程导致训练收敛误差较高,这不是我们期望的。动量可在神经网络当前变化的方向上对它施加一些力,让它突破局部最小值。
选择学习率和动量
动量和学习率有助于训练的成功,但实际上它们并不是神经网络的一部分。一旦训练完成,训练后的权重将保持不变,不再使用动量或学习率。它们本质上是一种临时的“脚手架”,用于创建训练好的神经网络。选择正确的动量和学习率会影响训练的效果。
学习率会影响神经网络训练的速度,降低学习率会使训练更加细致。较高的学习率可能会跳过最佳权重设置,较低的学习率总是会产生更好的结果,但是,降低训练速度会大大增加运行时间。在神经网络训练中降低学习率可能是一种有效的技术。
你可以用动量来对抗局部最小值。如果你发现神经网络停滞不前,则较高的动量值可能会使训练超出其遇到的局部最小值。归根结底,为动量和学习率选择好的值是一个反复试验的过程。你可以根据训练的进度进行调整。动量通常设置为0.9,学习率通常设置为0.1或更低。
Nesterov动量
由于小批量引入的随机性,SGD算法有时可能产生错误的结果。权重可能会在一次迭代中获得非常有益的更新,但是训练元素的选择不当会使其在下一个小批量中被撤销。因此,动量是一种资源丰富的工具,可以减轻这种不稳定的训练结果。
Nesterov动量是Yu Nesterov在1983年发明的一种较新的技术应用,该技术在他的Introductory Lectures on Convex Optimization: A Basic Course一书中得到了更新。
有时将该技术称为Nesterov的加速梯度下降。尽管对Nesterov动量的完整数学解释超出了本文的范围,但我们将针对权重进行详细介绍,以便你可以实现它。
下面公式基于学习率(ε)和动量(α)计算部分权重更新:
![]()
当前迭代用t表示,前一次迭代用t−1表示。这种部分权重更新称为n,最初从0开始。部分权重更新的后续计算基于部分权重更新的先前值。上面公式中的偏导数是当前权重下误差函数的梯度。公式下面公式展示了Nesterov动量更新,它代替了上上面公式中展示的标准反向传播权重更新:
![]()
上面的权重更新的计算,是部分权重更新的放大。上面公式中显示增量权重已添加到当前权重中。具有Nesterov动量的SGD是深度学习最有效的训练算法之一。