MATLAB绘图与图形

2D绘图基础

标签：

装扮图像;

线条风格

颜色说明符

添加图例

图象重叠和linspace命令

极坐标和对数图象

离散数据绘图

填充标记的样式

等高线图

装扮

三维图像：mesh(x, y, z)

装扮

2D绘图基础

装扮图像;

给图像添加网格：grid on
调整坐标轴：axis

axis square——>正方形图像

axis equal——>间距相同

axis auto ——> 自动选择

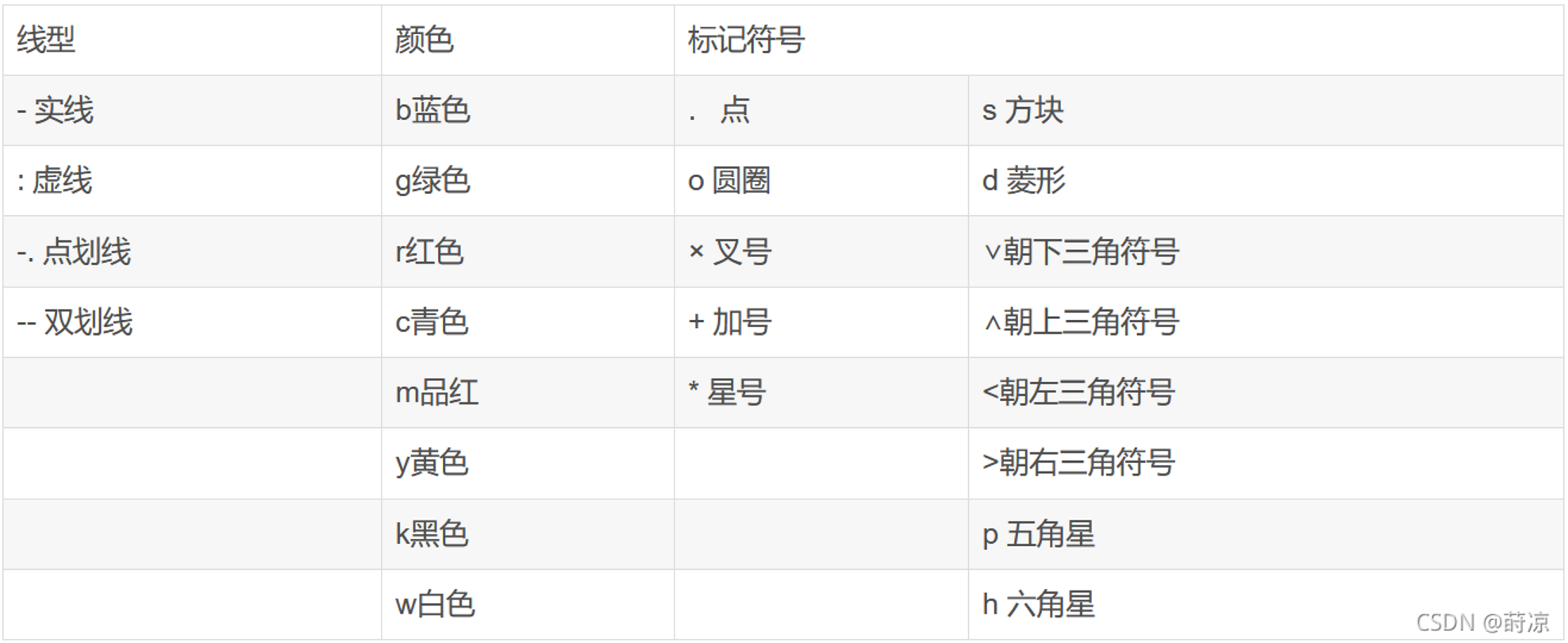
线条风格

z 实线 '-'
z 虚线 '--'
z 虚点线 '-.'
z 点线 ':'

颜色说明符

白色 w
黑色 k
红色 r
青色 c
蓝色 y
洋红 m
绿色 g
蓝色 b

添加图例

legend('sinh(x)','cosh(x)')

在同一图象中显示多个函数

plot(x, y)，一对一对的“x, y”，“x, y” 与“x, y”之间相互独立；单引号引起来绘制的第二条曲线风格的字符串

设置坐标比例

绘图范围: axis ( [xmin xmax ymin ymax] )

子图

subplot(m, n, p)

m 和n ：产生的子图有 m 行和 n 列，p ：要贴上去的某个已经绘制的图形窗口。

x = [0:0.01:5]; 
y = exp(-1.2*x).*sin(20*x); 
subplot(1,2,1)
plot(x,y),xlabel('x'),ylabel('exp(-1.2x)*sin(20x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(20*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(20x)'),axis([0 5 -1 1])

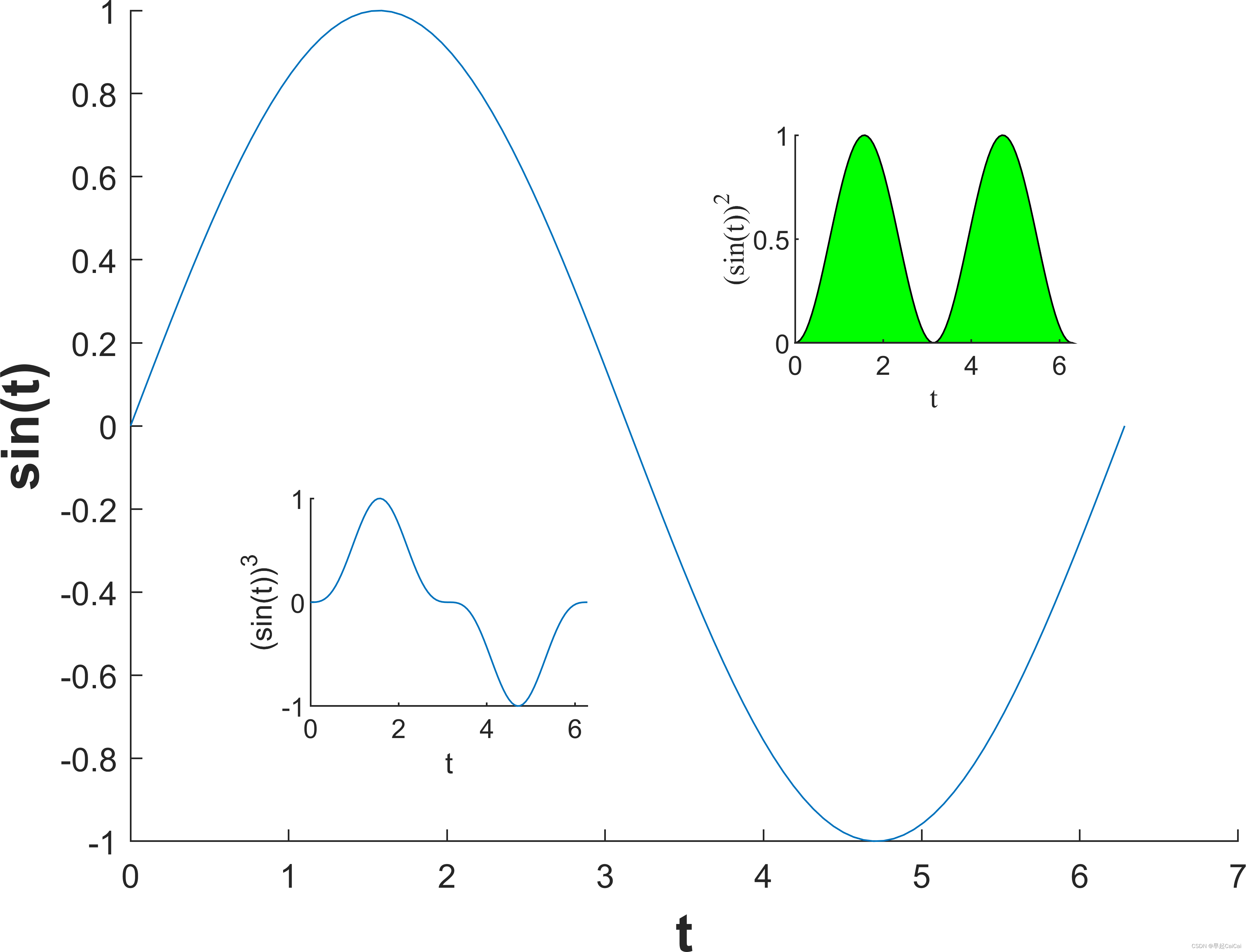
**图象重叠和*linspace***命令

x = linspace(a,b)

MATLAB 会在 a 到 b 间取出均匀分布的 100 个点（或行向量），如果写成

x = linspace(a,b,n)

那么 MATLAB 会在 a 、 b 之间取出均匀分布的 n 个点。

图象重叠 hold on

 x = linspace(0,2*pi); plot(x, cos(x)),axis([0 2*pi -1 1]) hold on plot(x, sin(x)), axis ([0 2*pi -1 1])

极坐标和对数图象

极坐标图象的命令为：polar ( theta , r )

绘制一条螺线——称为阿基米德螺线：r = a θ

定义函数 r ( θ )：

a = 2

0 ≤ θ ≤2π theta = [0 : pi/90 : 2*pi]

r = a*theta;

绘制：

polar(theta,r), title(' 阿基米德螺线 ')

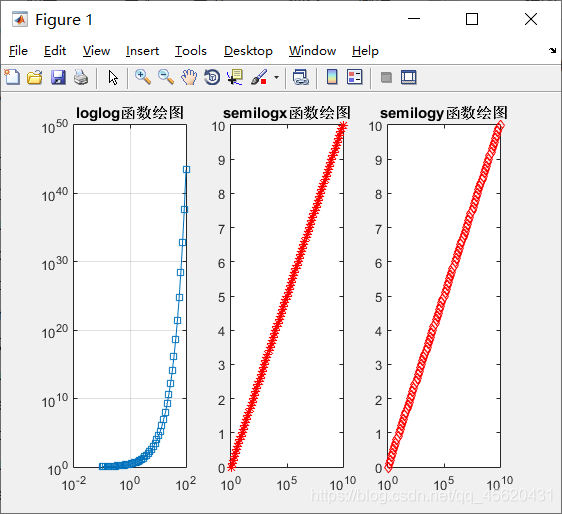
第一种我们能使用的对数图象是 log-log 图象

电路的频率响应，是输出对输八的比率（放大倍数）

用拉普拉斯变换，因此通常让 s = iω。
 RC = 0.25; s = [1:100]*i;F = abs(1./(1+RC*s)); %绝对值命令loglog(imag(s),F),grid,xlabel('频率 (rad/s)'), ylabel('输出/输入比'),title('频率响应')

离散数据绘图

例：学生名单和考试分数

1、plot()
% 定义两个数组
>> x = [1:5]; 
>> y = [50,98,75,80,98];
% 所要使用的标签：列表中用来设置姓名的元素必须具有相同的字符数。我们为每个学生分配一个 ID 码
['Adrian'; 'Jim';'Joe';'Sally';'Sue'] = ['001';'002';'003';'004';'005'] 
% 绘图
>> plot(x,y,'o',x,y),set(gca,'XTicklabel',['001'; '002';'003';'004';'005']), ... 
set(gca,'XTick',[1:5]),axis([1 5 0 100]),xlabel('学生'),ylabel('期末成绩'),title('2005 年 12 月期末考试')
2、二维条形图:bar(x, y)
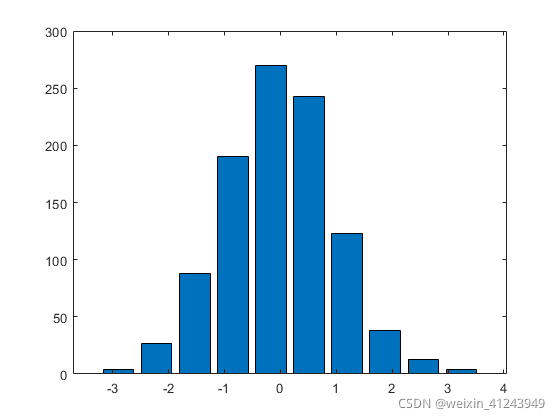
>> x = [1:5]; 
>> y = [50,98,75,80,98]; 
>> bar(x,y), xlabel('学生'),ylabel('分数'), title('期末测试')
3、针状图stem(x, y) :在每个点上都有一根条从水平轴或 x 轴延伸到该点，并且这些点用选择记号标示
>> t = [0: 5: 200]; 
>>  f = exp(-0.01*t).*sin(t/4);
>> stem(t,f),xlabel('时间(秒)'),ylabel('弹簧响应') 
'fill' 参数选项让 MATLAB 填充标记：stem(t,f,'--dg','fill'),xlabel('时间(秒)'),ylabel('弹簧响应')

填充标记的样式

方块(s)、菱形(d)、五角星(p)、圆圈(o)、叉号(x)、星号(*)和点号(.)

等高线图

1、简单绘制

>> [x,y] = meshgrid(-5:0.1:5, -3:0.1:3);
>> z = x.^2 + y.^2; 
>> contour(x,y,z)

2、说明标签 set（）

>> [C,h] = contour(x,y,z); 
>> set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)

3、三维 contour3(z,n) ：将产生有 n 个级别的等高线

>>  [x,y] = meshgrid(-2:0.1:2); 
>>z = y.*exp(-x.^2 - y.^2); 
>> contour(x,y,z),xlabel('x'),ylabel('y')

仅输入 contour3(x, y, z, 30),

装扮

>> surface(x,y,z,'EdgeColor',[.8 .8 .8],'FaceColor','none') 
>> grid off 
>> view(-15,20)

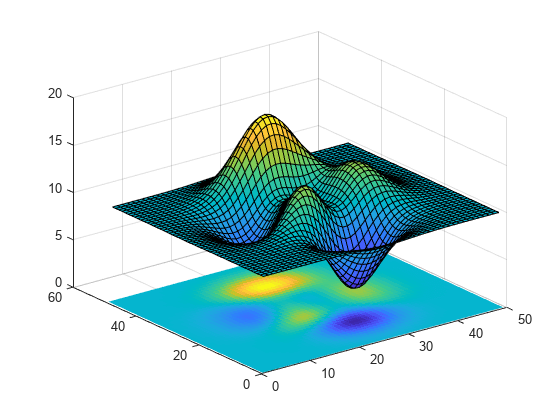
三维图像：mesh(x, y, z)

如上：z = ye^-(x 2 +y 2 )

>> [x,y] = meshgrid(-2:0.1:2); 
>> z = y.*exp(-x.^2-y.^2); 
>> mesh(x,y,z),xlabel('x'),ylabel('y'),zlabel('z') 
装扮

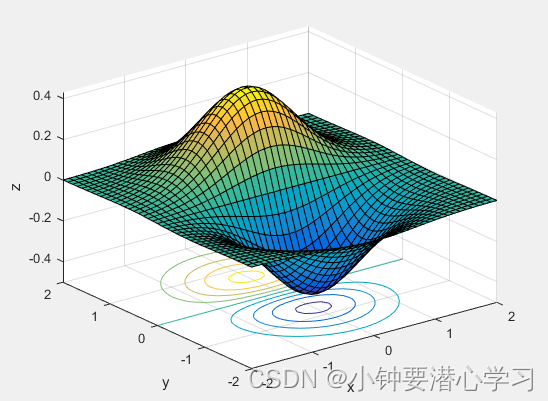
绘制制表面带有渐变颜色的图象： surf 或 surfc 命令
>> surf(x,y,z),xlabel('x'),ylabel('y'),zlabel('z') 
surfc
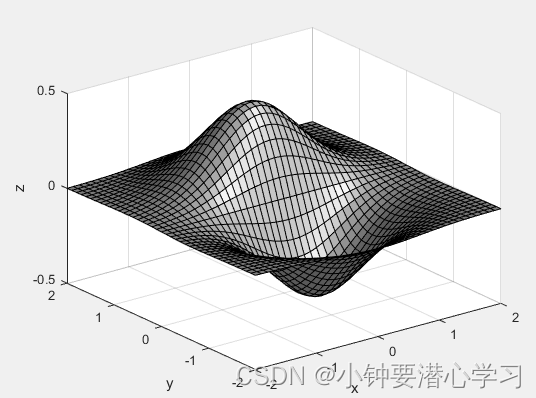
显示三维光照物体的表面 surfl（）
...
>> surfl(x,y,z),xlabel('x'),ylabel('y'),zlabel('z'); 
>> shading interp; 
>> colormap(gray);
图象中的阴影

flat 是用同一颜色为每个网格进行着色并隐藏网格线
facted 则显示网格
interp 是告诉 MATLAB 使用颜色插值的办法进行着色，因此显得非常平滑

flat:faceted: