1. 分类问题
回归与分类的区别:
- 回归可以用于预测多少的问题, 比如"预测房屋被售出价格",它是个单值输出。
- softmax可以用来预测分类问题,例如"某个图片中是猫、鸡还是狗?",这是一个多值输出,输出个数等于类别个数,输出的第i个值表示预测为第i类别的概率。
两者的区别在于是问多少还是问哪一个?
分类可以用来描述下面两个问题:
- 样本属于哪个类别
- 样本属于每个类别的概率
比较经典的分类问题有:
- MNIST数据集,手写数字识别,有0-9十个类别。
- ImageNet数据集,从一百万张图片中识别自然物体,有1000个类别。
- kaggle上的恶意软件类别识别。
- 区分淘宝商品的评论是正面还是负面评论。
2. 分类编码
由于自然语言表示的类别不方便运算,所以为了计算的需要,有必要对类别进行编码。
对于分类问题,最常用的编码方式为一位有效编码,也称为独热编码(one-hot encoding)。它可以表示为一个向量,长度等于类别数量,向量中只有一个特征为1,其它特征均为0。
这里我们以一个图像分类问题为例来讨论, 假设要预测一张图片是猫、鸡还是狗,那么我们对这三种类别进行一位有效编码的形式如下:
- (1,0, 0)对应于“猫”
- (0,1,0)对应于“鸡”
- (0,0,1)对应于“狗”
- 正确类别对应的分量设置为1,其它所有分量均为0.
- 类别数量等于分量数量(这里的分量是指向量在具体一个维度上的值)
分类问题对模型的要求:正确类的置信度要远远大于非正确类的置信度,即Oy > Oi。
相比具体每个类别的预测值大小,我们更关心正确类别的预测值是否远大于其它非正确类别的预测值,只有这样,才能表明模型能真正区分出正确类别。
3. 网络架构
与线性回归一样,softmax回归也是一个单层神经网络。
接着上面的例子,假设每次输入是一个2*2的灰度图像,我们可以用一个标量表示每个像素值,每个图像对应四个特征[x1,x2,x3,x4]。
我们可以定义输出向量y=[o1,o2,o3], 其中o1、o2、o3分别表示输入i是猫、鸡、狗的预测值大小。
由于我们有4个特征和3个可能的输出类别, 我们将需要12个标量来表示权重w, 3个标量来表示偏置b。则每个类别的计算可以表示为:
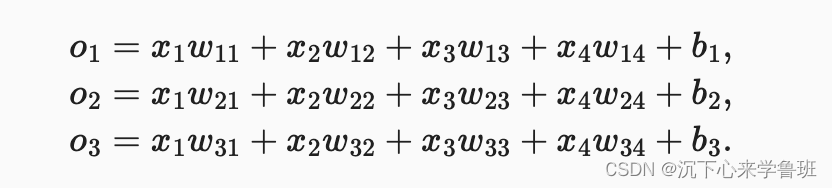
由于计算每个输出o1、o2和o3取决于 所有输入x1、x2、x3和x4, 所以softmax回归的输出层也是全连接层。
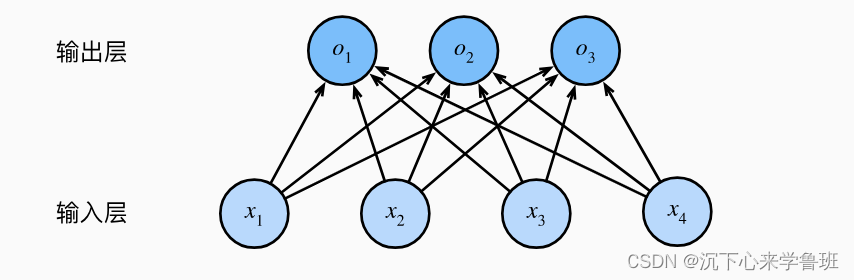
如同线性回归一样,可以将计算公式简洁表示,o = Wx + b。这是将所有权重放到一个W矩阵中。 对于给定数据样本的特征x, 我们的输出y是由权重W与输入特征x进行矩阵-向量乘法再加上偏置b得到。
4. 输出概率化
对于分类问题,我们希望模型的输出yj可以视为它属于类别j的概率,然后只需要选择具有最大输出值的类别argmax(xj,yj) 作为我们的预测即可, 这样能同时方便人脑理解和算术运算。
例如,如果为猫、鸡和狗的概率分别为0.1、0.8和0.1, 因为0.8概率最大,所以我们预测的类别是2,在我们的例子中代表“鸡”。
这里之所以要进行标准化概率计算,而不直接将预测o作为输出,其原因在于将线性层的输出o视作概率会存在一些问题:
- 线性层输出没有限制输出数字的总和为1,不符合概率分布。
- 根据输入的不同,线性层的输出是可以为负值的,会影响我们的计算。
要将输出视为概率,我们必须保证以下两点:
- 在任何类别上的输出都是非负
- 所有类别的预测值总和为1。
而softmax函数则正好能够将未规范化的预测变换为非负数并且总和为1,同时让模型保持可导的性质。它的作法为:
- 对每个未规范化的预测求幂(指数),这样可以确保输出非负
- 让每个求幂后的结果除以它们的总和,就能确保最终输出的概率值总和为1
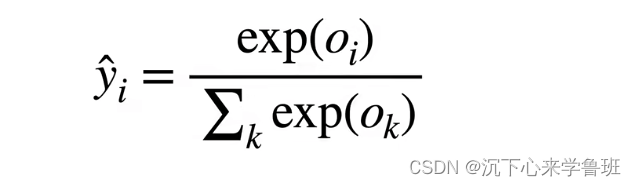 通过对输出向量o进行softmax运算后,预测值就是一个概率分布。
通过对输出向量o进行softmax运算后,预测值就是一个概率分布。
而真实的值经过独热编码后也符合这个特征,因为它也符合概率的特性:
- 非负数:只有0和1两种值;
- 和为1:只有一个值为1,其它均为0;
这样就得到两个概率:预测值概率和真实值概率。接下来,就可以比较两个概率来作为损失。
5. 损失计算
交叉熵损失:用来衡量两个概率分布之间的差异。
对于分类问题,我们不关心非正确类别的预测值,只关心对正确类的预测值置信度有多大。
假设模型对每个类别的预测概率分别是0.7、0.2和0.1,实际该样本属于第一个类别。交叉熵损失会根据模型对第一个类别的预测概率和实际概率来计算一个损失值。用数学表示如下:
H(p, q) = -Σ p(x) * log(q(x))
- p(x)表示实际的概率分布,q(x)表示模型预测的概率分布。
- 前面加负号的目的是为了保证交叉熵为正值。log(q(x))的值通常是小于0的(小于1时,对数为负数),p(x)是一个概率值,介于0和1之间。
- 交叉熵越小,表示两个概率分布越接近,模型的预测效果越好。
可以把交叉熵H(P,Q)想象为“主观概率为Q
的观察者在看到根据概率P生成的数据时的意外程度”。 当P=Q时,这种意外程度降到最低。
训练的目的:最小化交叉熵来优化模型的参数,使得模型的预测结果更接近于实际标签。
由于真实值p(x)是一个独热编码向量,只有一项为1,其它项均为0,所以这里的交叉熵又可以简写成:
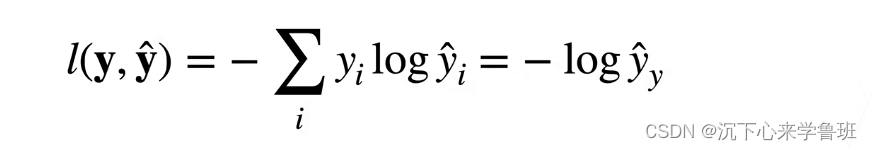
所以,对于分类问题来说,我们不关心非正确类别的预测值,只关心正确类别的预测值有多大。
而梯度则是预测概率与真实概率之间的差异,损失函数对输出o求导为:
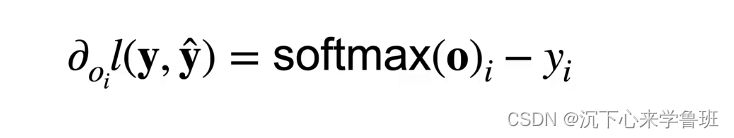
softmax回归模型训练的目标:给出任何样本特征,我们可以预测每个输出类别的概率。 通常我们使用预测概率最高的类别作为输出类别。 如果预测与实际类别(标签)一致,则预测是正确的。