基于树的模型是机器学习中非常重要的一类模型，最基础的就是决策树，本篇主要讲述决策树的原理和几类最常见的决策树算法，这也是更复杂的树模型算法的基础。

参考文章：
1.CSDN-基于熵的两个模型(ID3,C4.5)比较详细，有数字例子

2.腾讯云-基于基尼指数的模型(CART)比较详细，有数字例子

3.知乎-在CART剪枝这里比较详细

1.原理

首先给出集中集中常见决策树算法的对比：

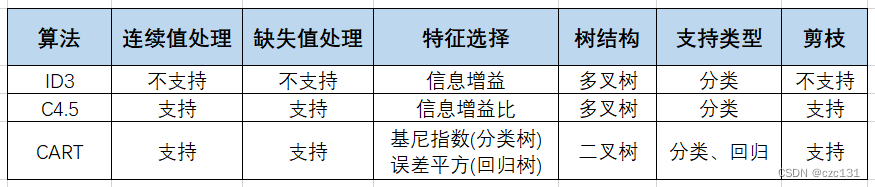
下面展开叙述。

1.1.基于熵

1.1.1.熵

熵最常用在信息学里面，是一种表示不确定性的度量。
假设对于随机变量$X$存在分布$P(X=x_i)=p_i，i=1,2,...,n$，此时定义熵：
$$H(X)=H(p)=-\sum _{i=1}^n{p}_{i}lo{g}_a{p}_i$$其中，$H(X)=H(p)$是因为结果只和分布有关，对于$log$的底$a$，可以为$2,e...$。

若$a\ge 1$,存在等式：
$$0\le H(x)\le lo{g}_{a}n$$左显然成立（和$a$无关），因为$p_i\le 1$，那么$-lo{g}_a{p}_i\ge 0$，求和后依然成立。

右边的根据博客的说法：

熵越大代表随机变量的不确定性越大，当变量可取值的种类一定时，其取每种值的概率分布越平均，其熵值越大。

也就是分布非常平均，此时每个都是$\frac{1}{n}lo{g}_{a}n$，此时取得最大熵$lo{g}_{a}n$（也就是不确定性最大，通俗理解也就是没给出任何信息，因为本身$n$件事的先验分布就是均匀分布）。

下面是补充的一些概念：

• 若 p=0 ，则定义 0log⁡0=0 。
• 对数以 2 为底熵的单位为比特（bit）
• 对数以 e 为底熵的单位为纳特（nat）

1.1.2.条件熵

条件熵表示在已知$X$的条件下对$Y$不确定性的度量。首先假设$X,Y$的联合分布为：$​
$$P(X=x_i,Y=y_j)=p_{ij},i=1,2,...,n，j=1,2,...,m$$那么$Y$关于$X$的条件熵$H(Y|X)$就是：
$$\begin{gathered} H(Y|X=x_i)=\sum _{i=1}^{n}P(X=x_i)H(Y|X=x_i) \\ =\sum _{i=1}^{n}P(X=x_i)\sum _{j=1}^m-P(Y=y_j|X=x_i)logP(Y=y_j|X=x_i) \end{gathered}$$（省略掉了$log$的底$a$）

1.1.3.熵的意义

前面讲了熵和条件熵的计算，在这里结合一个实例来记录熵的意义。

比如有下面这个关于贷款统计的统计表：

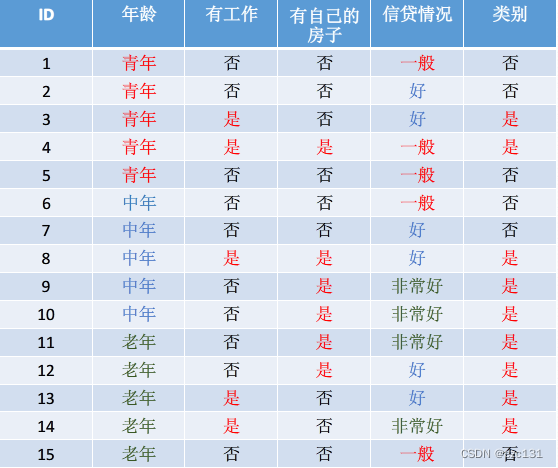
那么假如要计算类别的熵，在一开始没分类的情况下，$H(D)$的计算如下：
$$H(D)=-(\frac{6}{15}log\frac{6}{15}+\frac{9}{15}log\frac{9}{15})=0.971$$这就是一开始的不确定性为0.971，而分类的目标就是利用相应的特征，使得为是和为否的样本在不同的子集中，可以想象，加入类别全是为是，那么此时$H(D)=1log1=0$，这也就消除了全部的不确定性。

为了达到分成不同子集的目标，引入了条件熵，而分类的依据被称作特征，对应了条件熵中的$X$，假设现在根据年龄来划分，年龄对应了青年、中年和老年，分别计算对应的条件熵$H(D|X)$，设青年、中年和老年分别为$x_1、x_2、x_3$：
$$\begin{gathered} H(D|X=x_1)=P(X=x_i)H(D|X=x_1) \\ =\frac{5}{15}(-\frac{2}{5}log\frac{2}{5}-\frac{3}{5}log\frac{3}{5})+\frac{5}{15}(-\frac{3}{5}log\frac{3}{5}-\frac{2}{5}log\frac{2}{5})+\frac{5}{15}(-\frac{4}{5}log\frac{4}{5}-\frac{1}{5}log\frac{1}{5}) \\ =0.888 \end{gathered}$$也就是特征$X$的引入，使得分类结果的不确定性从$H(D)=0.971$变为了$H(D|X)=0.888$，这也就说明分类结果变得更加确定，通过不断加入特征，减少分类结果的熵，从而得到正确的分类器。

1.1.4.ID3

ID3是一种基于信息增益的分割方式，信息增益定义为$g(Y|X)$，如下：
$$g(Y|X)=H(Y)-H(Y|X)$$每次选择信息增益减少最多的进行分裂。但是这样会导致一个结果，假设有一个类别有很多种类，比如15个样本有15个种类，那么分类器就会分出15个类别，这样可以将每个类别的熵减少到0，完全确定，但是显然这个分类器深度过浅且过于庞大，不利于模型的泛化，此时可以设定$\alpha$，对小于增益小于阈值的进行剪枝。

1.1.5.C4.5

C4.5主要为了改善上面提到的单特征多类别的问题，定义信息增益比，记为$g_R(Y|X)$，如下：
$$g_R(Y|X)=\frac{H(Y)-H(Y|X)}{H(Y)}$$此时如果$Y$的类别很多，那么其熵$H(Y)$就会增大，那么此时信息增益比就会变小，那么就不会有限选择这样的特征进行分裂。

ID3和C4.5生成的都是多叉树分类器，基于熵的算法只能用于分类任务，不能用于回归任务。

1.2.基于基尼指数

1.2.1.基尼指数

在分类问题中，假设存在$n$种类别，每个类别为$x_i$，存在概率分布：
$$P(X=x_i)=p_i,i=1,2,3,...,n$$将基尼指数记为$Gini(p)$，如下：
$$Gini(p)=\sum _{i=1}^n{p}_i(1-p_i)=1-\sum _{i=1}^n{p}_i^2$$可以发现，假如此时存在一个类别，那么$p_i=1$，此时基尼指数为0，确定性最强；要是有两个类别，概率平均分配，那么$Gini=1-0.5^2-0.5^2=0.5$，这和熵类似，都是不确定性的度量，被称为纯度，Gini越小，纯度越高。

1.2.2.CART分类

下面是关于使用$Gini$指数进行分类。

CART分类树的生成基于$Gini$指数。

假设当前分裂的集合$D$中包含$K$个样本，每次选择一个特征的一个值$A$，将样本分为是该值/不是该值的两部分，记为$D_1/D_2$，计算该特征对应的基尼指数：
$$Gini(D,A)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$$其中$|D|$表示样本集的数量。

下面以一个例子来说明，还是上面的贷款数据集，假设现在要计算年龄特征，年龄特征分别是青年、中年、老年，分别记为$A_1,A_3,A_3$，先计算$Gini(D,A_1)$，此时$D_1$对应为青年的样本，有5个，$D_2$对应不为青年的样本，有10个。

计算如下：
$$\begin{gathered} Gini(D_1)=\frac{2}{5}(1-\frac{2}{5})+\frac{3}{5}(1-\frac{3}{5}) \\ Gini(D_2)=\frac{7}{10}(1-\frac{7}{10})+\frac{3}{10}(1-\frac{3}{10}) \\ Gini(D,A1)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)=\frac{5}{15}Gini(D_1)+\frac{10}{15}Gini(D_2) \end{gathered}$$每个$Gini(D_i)$都是在计算分类节点内样本所有类别（比如贷款/不贷款或者还有更多类别）对应的和。

在找出$Gini$指数最小的那个分裂点之后，将其作为最优切分点，继续分裂，对于$Gini$指数已经为0的，这样的样本已经很纯（内部只有一个类别），因此无需继续分裂。

这样不断迭代，算法停止计算的条通常是节点中的样本点个数小于设定阈值，或样本集合的基尼不纯度小于设定阈值，亦或是没有更多特征，这一点同ID3和C4.5算法的停止条件类似。

1.2.3.CART回归

上面的是分类的做法，不同于基于熵的做法，基于$Gini$指数的CART算法可以用于回归任务。

回归任务一般的目标就是和标签值越越接近越好。跟线性回归类似，CART的损失函数如下：
$$L(y,\hat{y})=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$CART用于回归的思想：不断把区间按照一定的规则一分为二，给切分后的区间分别置为最优输出值，计算出每种切分方式的损失，选出损失最少的规则进行切分，然后对残差继续切分，不断迭代。

表达式如下：
$$\underset{j,s}{\min }(\sum _{i=1}^s(y_i-C_1{)}^2+\sum _{i=s+1}^n(y_i-C_2{)}^2)$$其中$j,s$表示第$j$个变量的分裂点$s$（因为是一分为二，所有有个分裂点），分为两个集合$R_1,R_2$，$C_1,C_2$分别是$R_1,R_2$的最优取值，也就是位于这个集合之内的值都是这个，可以是对应集合所有值的均值。

下面举个例子：

比如有一个回归任务如下：

$x$	1	2	3	4	5	6	7	8	9	10
$y$	5.56	5.70	5.91	6.40	6.80	7.05	8.70	8.90	9.00	9.05

首先先确定分割点，定义为$z=(x_i+x_{i+1})/2,i=1,2,...,9$，也就是$1.5,2.5,...9.5$，取其中一个值，那么$x$就被分为两个部分，分别是$1--int(z)$和$int(z)+1--10$。

比如对于$z=1.5$，此时两个集合分别对应 R 1 = { x ∣ 1 } R_1={\{x|1\}} R1​={x∣1}和 R 2 = { x ∣ 2 , 3 , . . . , 9 } R_2={\{x|2,3,...,9\}} R2​={x∣2,3,...,9}，均值分别为$5.56,7.50$，这也就对应了$C_1,C_2$，代入公式计算损失：

$$\begin{gathered} (\sum _{i=1}^s(y_i-C_1{)}^2+\sum _{i=s+1}^n(y_i-C_2{)}^2) \\ =(\sum _{i=1}^1(y_i-5.56{)}^2+\sum _{i=2}^{10}(y_i-7.50{)}^2)=15.72 \end{gathered}$$同理，可以计算其他所有分割方式的损失，得到：

可以看到等于6.5的时候得到了最小的损失，因此将6.5作为第一个分割点，得到如下分割规则：
$$f(x)=T_1(x)=\{\begin{array}{c}6.24,x\le 6.5\\ 8.91,x＞6.5\end{array}$$（这里的$6.24$是$1-6$的均值，$8.91$是$7-10$的均值）

由此规则可以计算出所有点的残差：

此时按照上面的规则再对残差进行分割，得到在3.5的时候有最小的损失，即
$$T_2(x)=\{\begin{array}{c}-0.52,x\le 3.5\\ 0.22,x＞3.5\end{array}$$将$T_2$和$T_1$进行叠加，得到新的分类结果：
$$f(x)=\{\begin{array}{c}5.72,x\le 3.5\\ 6.46,3.5＜x\le 6.5\\ 9.13,x＞6.5\end{array}$$其中这里的$5.72=6.24-0.52$，下面的同理，就是跟前面的叠加。

重复这样的过程，就可以得到回归树。

1.3.连续数据

离散化

前面讲的分类都是离散数据，但是实际情况中存在连续数据，那么和前面CART的回归类似，先将序列排序，然后计算$z$序列，$z$序列为相邻两值的均值，然后形成$n-1$个分裂点，这就可以看做前面的若干类别，那么就跟离散变量是一致的了。（取小于该值和大于该值的作为两个集合，相当于两个类别）

1.4.剪枝

下面是关于剪枝的部分，因为树模型不断的分裂，很有可能形成一个很复杂的分类树，那么就需要对模型进行剪枝，下面是一种剪枝方式。

下面提出误差率的概念，误差率表示预测错误的占总数的比例，定义为
$$C(t)=\frac{nu{m}_{err}}{num}$$其中，$t$为某决策树，$nu{m}_{err}$表示该决策树在训练集上预测错误的数量（数量最大的为预测类别，和标答不一样的都是预测错误的），$num$表示样本总数。

在剪枝的过程中，将损失函数变形为：
$$C_a(T)=C(T)+a|T|$$其中$|T|$表示叶子结点的个数，$a$是一个系数，需要计算得到。这个表达式本质就是在计算对一个节点（只关注这一个节点）进行分裂之后，每多一个叶子，多一个惩罚项$a$。

可以看到，若$a=0$，那么就是原来的损失函数，因为分裂的越多，准确率也越高，那么最终一定会倾向于有很多叶子结点；若$a->+\infty$，此时一旦分裂，就会有很大的惩罚项，那么就倾向于不分裂。这个中间存在一个值$a^{\ast }$使得：
$$\begin{gathered} C_a(t)=C(t)+a^{\ast } \\ {C}_a(T_t)=C(T_t)+a^{\ast }|T| \\ {C}_a(t)=C_a(T_t) \end{gathered}$$其中$t$为剪枝后的决策树（只有一个叶子结点，所以是$a^{\ast }$），$T_t$为剪枝前的决策树（有$|T|$个叶子节点），$C_a$为其对应在训练集的误差率。

这几个式子表明存在一个值$a^{\ast }$使得分裂前和分裂后的误差函数相同，联立可解$a^{\ast }$：
$$a^{\ast }=\frac{C(t)-C(T_t)}{|T|-1}$$对于每个非根节点且非叶子的节点，都计算这个值$a^{\ast }$，形成一个序列，选出最小的那个进行剪枝。

为什么选最小的，$a^{\ast }$对应的剪枝前后的树的损失函数是一样的，由上面的$a^{\ast }$的计算式子，如果$a^{\ast }$比较小，因为$C(T_t)$是一样的（剪枝前大家都一样），那么要么是$C(t)$比较小（剪枝后误差比较小），要么是$|T|$比较大（剪枝前叶子比较多），这两种情况都应该把节点给剪枝。

对于每个节点，计算剪枝前后误差率之差（也就是节点误差率-叶子误差率之和），选出误差率最小的，然后剪枝。

这是一个具体过程，也就是计算a的过程，就不详细展开了。（但是个人感觉计算有点冗余）

2.代码

下面是代码实现的部分，写了一个基于CART的分类树，使用的样本就是上面提到的贷款数据，数据如下图：

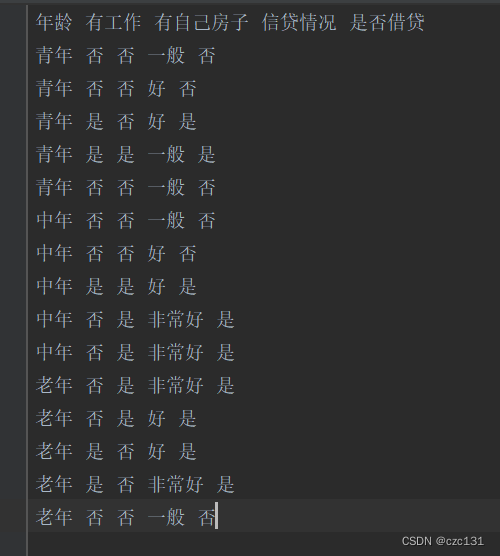
是一个.txt文档，运行后得到了分类的结果，最终分类的几个集合都只有一个类别，也就是根据这些分类规则，可以完全将数据分开。

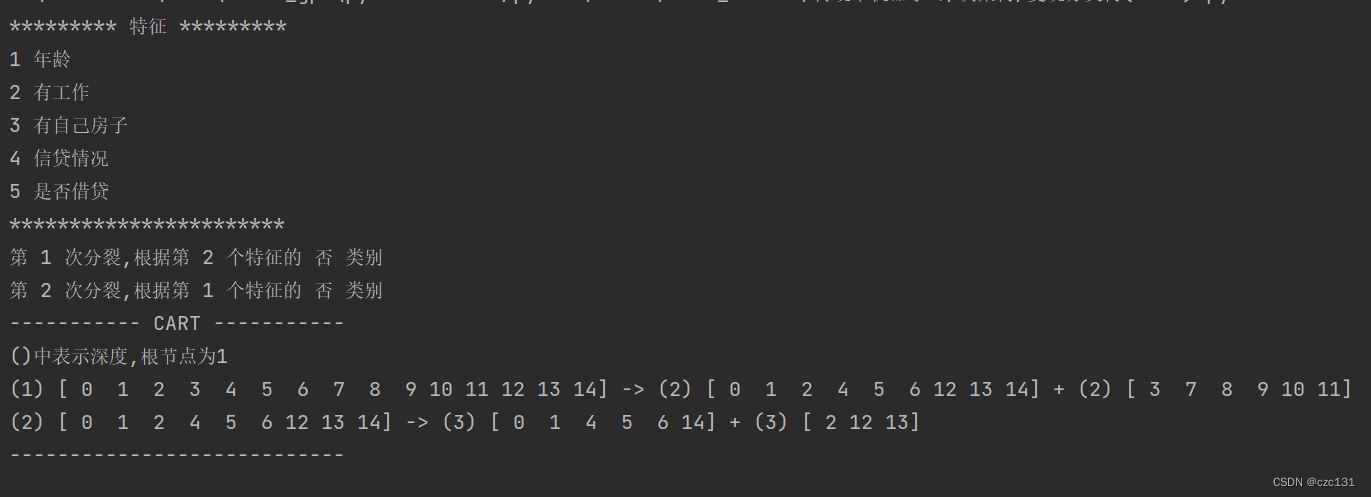
完整代码

# 基于CART的决策分类树复现(离散)
import collections
import queue
import numpy as np
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falsedef load_data():with open('static/data.txt', mode='r', encoding='utf-8') as f:data=f.read().split('\n')title=data[0].split(' ')x=[]y=[]for i in range(1,len(data)):xy = data[i].split(' ')x.append(xy[:-1])y.append(xy[-1]) # 最后一个是标签x = np.array(x)y = np.array(y)return title,x,yclass Node():def __init__(self,node_id=0,deep=0,id_list=None,nxt_list=None,split=True):self.node_id=node_idself.deep = deepif id_list is not None:self.id_list = np.array(id_list,dtype=int)  # 当前节点的索引集合else:self.id_list=[]if nxt_list is not None:self.nxt_list = np.array(nxt_list)  # 当前节点的索引集合else:self.nxt_list=np.array([])self.split=split # 是否需要继续分裂class CART():def fit(self,x,y,gini_thresh=0.1):samples = x.shape[0]features = x.shape[1]root = Node(node_id=0,deep=1,id_list=np.arange(samples),nxt_list=[],split=True)# 先统计y的相关信息y_cag = collections.Counter(y)# print('标签统计信息:',y_cag)# label_list = list(y_cag.keys()) # y的所有类别tree = [root] # 存储最终的树q = queue.Queue() # 产生一个队列q.put(root)split_cnt = 0 # 记录分裂次数while not q.empty(): # 取出一个节点node = q.get() # 移除并返回数据id_list = node.id_list # 得到当前集合的所有idlabel_num = collections.Counter(y[id_list]) # 当前集合样本的所有对应标签的样本数num_all = id_list.size # 单管集合的所有数据min_gini = [0,None,0x3f3f3f3f,[],None] # 记录当前集合feature索引和特征名称(分裂信息),以及对应的gini指数,还有集合idfor i in range(features): # 对于每个feature选择# 求出所有特征类别和对应的idfeat_dict = {}# 这个地方有问题(不应该统计所有样本,而是当前对应的,应该可以在上面的id循环里面统计掉)for idx in id_list:if x[idx,i] not in feat_dict.keys():feat_dict[x[idx,i]]=[] # 当前id(索引)feat_dict[x[idx, i]].append(idx)# 下面枚举将当前特征特征的每个取值作为分割点for type in feat_dict.keys(): # type作为分割点(统计分割点内的个样本匹配数量)res = {}for idx in feat_dict[type]:if y[idx] not in res:res[y[idx]]=0res[y[idx]]+=1# 根据统计出的数量已经可以计算基尼系数 gini=1-∑p^2num = len(feat_dict[type]) # 得到数量(为是的)gini_D1 = 1for key in res.keys():gini_D1-=(res[key]/num)**2gini_D2 = 1if num_all!=num:for key in label_num.keys(): # 利用集合总数来推算为否的集合ginisub = 0 # 要减去的样本(在集合D1的)if key in res.keys():sub = res[key]gini_D2-=((label_num[key]-sub)/(num_all-num))**2gini = (num/num_all)*gini_D1+((num_all-num)/num_all)*gini_D2if gini<min_gini[2]:min_gini[0]=imin_gini[1] = type # 第i个特征的类别typemin_gini[2]=ginimin_gini[3] = feat_dict[type] # 记录idmin_gini[4]= (gini_D1,gini_D2) # 记录两个集合的gini决定是否继续分裂# 找到最小的gini进行分裂split_cnt+=1# print('总样本集:',id_list)print('第 %d 次分裂,根据第 %d 个特征的 %s 类别'%(split_cnt,min_gini[0],min_gini[1]))id_D1 = min_gini[3]id_D2 = []# print(id_list)for id in id_list:if id not in id_D1:id_D2.append(id)# 生成两个节点id1 = len(tree)id2 = len(tree)+1 # 即将插入的两个节点的id(也就是在tree中的索引)tree[node.node_id].nxt_list=[id1,id2]node1 = Node(node_id=id1,deep=node.deep+1,id_list=id_D1,nxt_list=[])node2 = Node(node_id=id2,deep=node.deep+1,id_list=id_D2,nxt_list=[])# 判断是否需要继续分裂(纯度,纯度也就是如果都是一个类别为0就不分裂,还有个用阈值计算,懒得算了)if min_gini[4][0]<gini_thresh:node1.split=False # 无需分裂else:q.put(node1)if min_gini[4][1]<gini_thresh:node2.split=False # 无需分裂else:q.put(node2)tree.append(node1)tree.append(node2)# print(tree)self.tree  = treedef printTree(self):tree = self.treeprint('----------- CART -----------')print('()中表示深度,根节点为1')for subtree in tree:if subtree.split:print('(%d)'%(subtree.deep),subtree.id_list, end='')print(' -> ',end='')node1 = tree[subtree.nxt_list[0]]print('(%d)'%(node1.deep),node1.id_list,end=' + ')node2 = tree[subtree.nxt_list[1]]print('(%d)'%(node2.deep),node2.id_list)print('----------------------------')if __name__ == '__main__':title,x,y = load_data()print('********* 特征 *********')for i in range(len(title)):print(i+1,title[i])print('***********************')dct_cart = CART()dct_cart.fit(x,y)dct_cart.printTree()