一、说明

我相信你们中的许多人都熟悉微分方程，或者至少知道它们。微分方程是数学中最重要的概念之一，也许最著名的微分方程是布莱克-斯科尔斯方程，它控制着任何股票价格。
​​
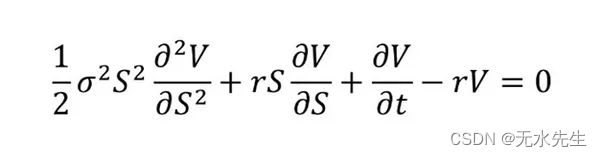
股票价格的布莱克-斯科尔斯模型

微分方程可以由数学中的许多想法组成，今天我将介绍一个涉及矩阵的微分方程。在研究解决方案时，我希望您能获得一些关于我们如何处理新概念的知识。我还将努力确保每个步骤都有合适的动机，以确保我们能够理解我们方法的直觉和发展。

二、矩阵微分方程

在我们的求解过程中，我们将介绍两种非常相似的求解方程的方法。

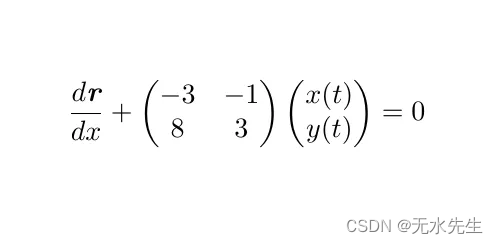
请注意，r 是涉及 x（t） 和 y（t） 的向量

那么从哪里开始呢？有些人可能很想将矩阵相乘，但是，我认为我们可以看到，这不会让我们无处可去。相反，让我们快速让 A 成为 2x2 矩阵，并用 r 代替我们的列向量来获得。

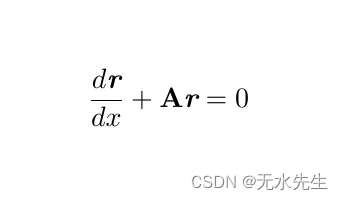
这种形式可以帮助我们决定我们采取的方法，因为这种形式看起来与我们以前遇到的微分方程非常相似。我们有一个常数，矩阵 A 和我们的因变量 r。忽略我们将向量和矩阵作为我们的系数和变量并稍微改变变量的事实，我们将如何解决这个微分方程：

其中 a 是某个常数。有多种方法可以解决这个问题。一种更简单的方法是简单地猜测 r 在 x 中的形式，注意我们有一个 r 的导数与 r 成正比。然后我们可以推断出一般形式是 r = Cexp（λx）。然后，我们可以用它代替 r 和 dr/dx 来找到 λ，然后，如果我们给定初始条件，我们可以找到常数 C。

那么，为什么不用我们原来的微分方程来试试呢？我认为我们有足够的动力去尝试。一些敏锐的读者可能还会注意到，我们的常量最终会成为矩阵，但我们会在工作原理中看到原因。

现在请注意，我们不能让 Mexp（λt） 等于 0，因此我们必须让 λ+A=0。

但是等等！我们已提升到矩阵。这怎么行得通？在这一点上，有些人可能会认为这是行列式，我们的方法失败了。让我们回想一下 exp（x） 的 Maclaurin 级数

大多数读者只会看到 x 是一个实数，也可能是一个复数。但是让 x 成为矩阵似乎几乎是非法的。尽管如此，让我们试试吧，我们没有什么可失去的！

我们需要首先计算矩阵 A 的一些幂，以代入我们的级数展开。

这看起来不错。所以现在让我们代入麦克劳林级数中 A 的这些幂，看看我们得到了什么

​
希望你和我一样觉得这个结果令人满意。如果你想了解更多关于将 e 提升到矩阵的信息，这里有一篇关于将 e 提升到矩阵的漂亮结果的文章：将欧拉数提升到矩阵。

所以现在我们可以说

​
为了找到我们的矩阵 M，我们必须有 r 满足的初始条件。假设我们有条件

将这些条件代入 r 的表达式中，我们可以得到 M，但我们很快就会遇到问题

请注意，我们可以将矩阵 M 后乘以 2x2 矩阵得到 2x1 矩阵。相反，我们必须切换 M 和我们的 2x2 矩阵才能使乘法有效。最后，我们得到 M

我们可以将这个 M 代入 r 的表达式中，我们得到微分方程的解。

多么美妙的结果。很快，我想展示一种类似方法来求解微分方程的开始，这也很好地说明了为什么我们需要在 exp（-At） 的右侧使用矩阵常数 M。

四、因式分解

再次考虑我们的微分方程

让我们使用积分因子来求解这个方程。因此，我们的首要任务是找到积分因子，如果你还记得的话，它是 exp（P（x）），其中 P（x） 是 x 的函数，乘以广义微分方程中的因变量

所以在这里，我们的 P（x） 只是矩阵 A，它是一个常数。

请注意，在计算积分时，我们不必担心积分常数

这看起来很熟悉，不是吗？我们现在知道不要害怕 e 上升到矩阵。因此，让我们计算这个积分因子

然后，我们将微分方程乘以这个积分因子，得到一个“完美导数”，确保我们记住我们正在处理矩阵，因此不满足交换性。所以我们必须保持乘法的顺序不变

请注意，当我们接管 exp（At） 时，因为这是一个矩阵，我们必须预先乘以它的倒数。这为我们提供了现在 RHS 上的正确顺序，因此如果 M 是 2x1 矩阵，我们将获得 r 的正确维度矩阵。要计算 RHS 上矩阵的逆，我们可以简单地用普通方法完成

这导致我们得到一个熟悉的 r 表达式，其乘法顺序正确

代入我们的条件会得到与我们之前相同的矩阵 M。

微分方程的解有两种不同的方式。我希望你学到了一些新东西，并看到了我们如何解决不熟悉的问题。

​

​