MATLAB 基于规则格网的点云抽稀方法（自定义实现）（65）
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/322256.html
如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
为什么你创业总是失败？2024普通人如何创业？2024创业赛道！2024创业新风口！2024创业方向！2024普通人的机会！
为什么你做项目老是不赚钱，是你不够努力吗？是你运气不好吗？
如果都不是！那一定是你的思维逻辑出了问题！
先想一想你以前做的项目，有没有哪个符合以下条件：对客户有价值、寻找客源成本在可接受…
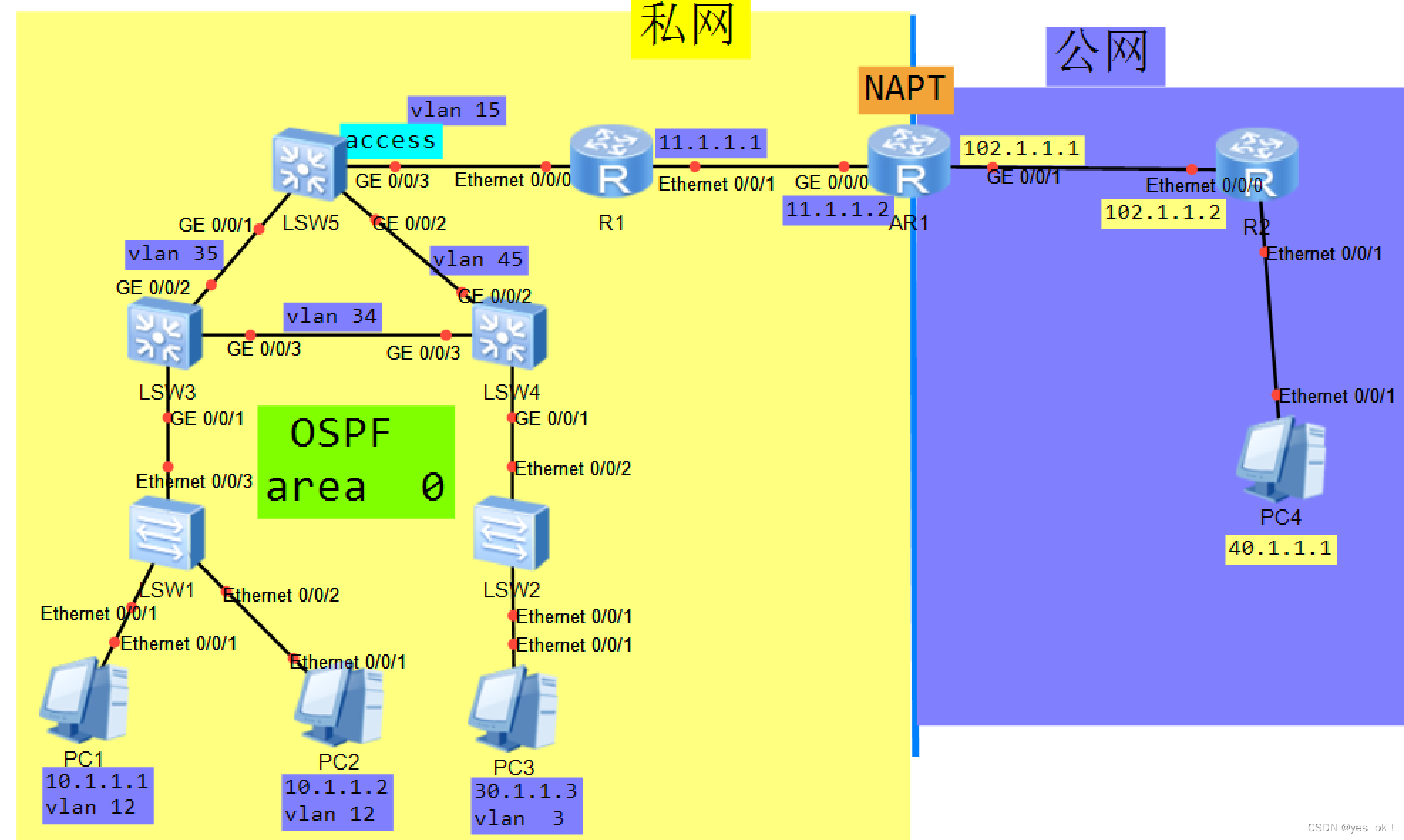
华为eNSP综合实验-网络地址转换
实验完成之后，在AR1的g0/0/1接口抓包，查看地址转换
实现私网pc访问公网pc
实验命令展示 SW1： vlan batch 12 #创建vlan interface e0/0/1 #进入接口配置vlan端口 port link-type access port default vlan 12 q interface e0/0/2 #进入接口配置vlan端口 port link-type ac…
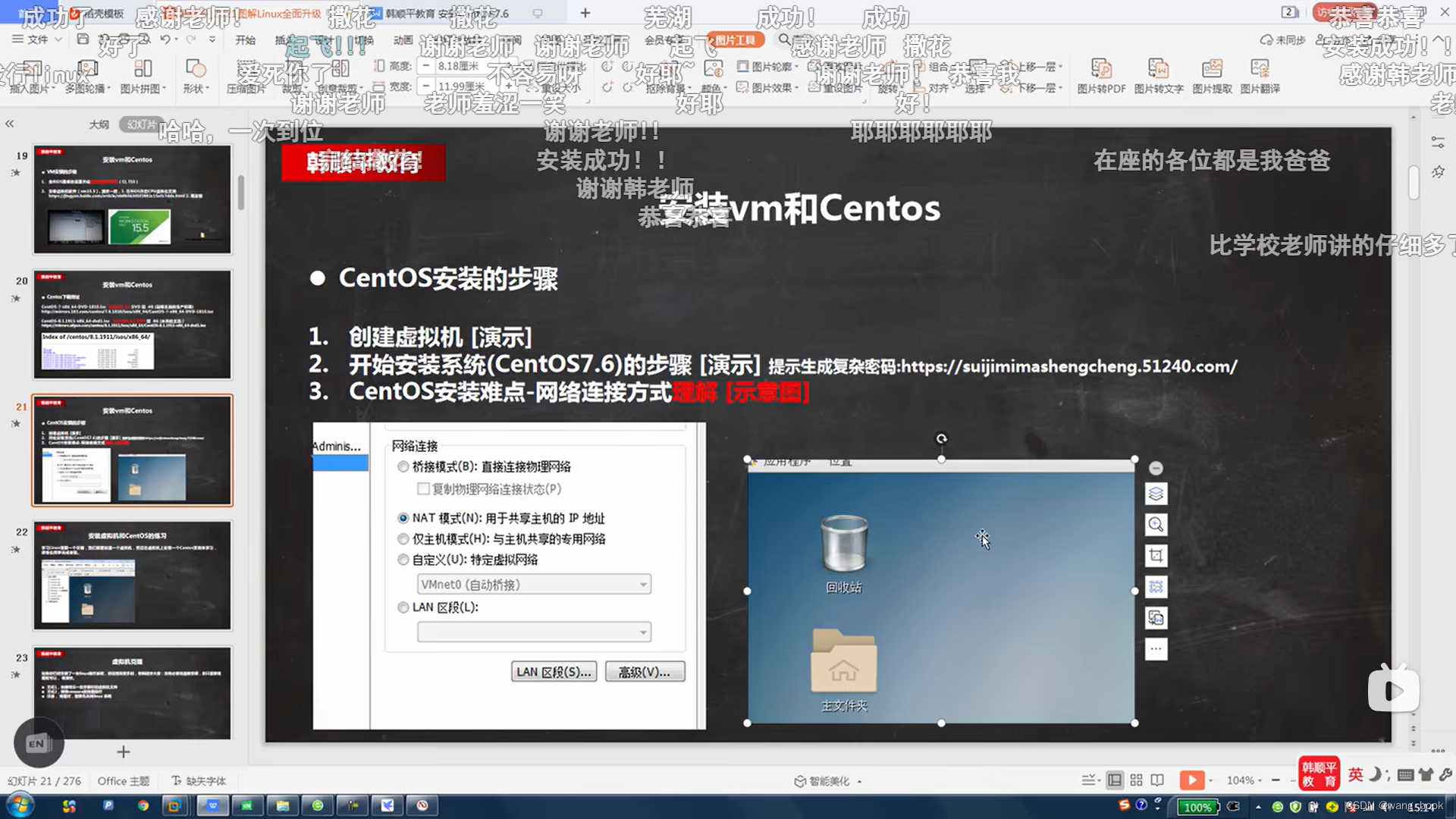
Linux高级学习（前置 在vmware安装centos7.4）
【小白入门 通俗易懂】2021韩顺平 一周学会Linux
此文章包含第006p-第p007的内容 操作
在安装好的vmware下进行安装 这里使用的是vmware15（win10下），win11可能无法使用15（有几率蓝屏），换成16就行了 用迅雷…
（二刷）代码随想录第1天|704. 二分查找 27. 移除元素
704. 二分查找 704. 二分查找 - 力扣（LeetCode） 代码随想录 (programmercarl.com) 手把手带你撕出正确的二分法 | 二分查找法 | 二分搜索法 | LeetCode：704. 二分查找_哔哩哔哩_bilibili 给定一个 n 个元素有序的（升序）…
微信小程序个人中心、我的界面（示例四）
微信小程序个人中心、我的界面，九宫格简单布局（示例四）
微信小程序个人中心、我的界面，超简洁的九宫格界面布局，代码粘贴即用。更多微信小程序界面示例，请进入我的主页哦！
1、js代码
Page({…
无意的一次学习，竟让我摆脱了Android控制？
由于鸿蒙的爆火，为了赶上时代先锋。到目前为止也研究过很长一段时间。作为一名Android的研发人员，免不了对其评头论足，指导文档如何写才算专业？页面如何绘制？页面如何跳转？有没有四大组件等等。
而Harmony…
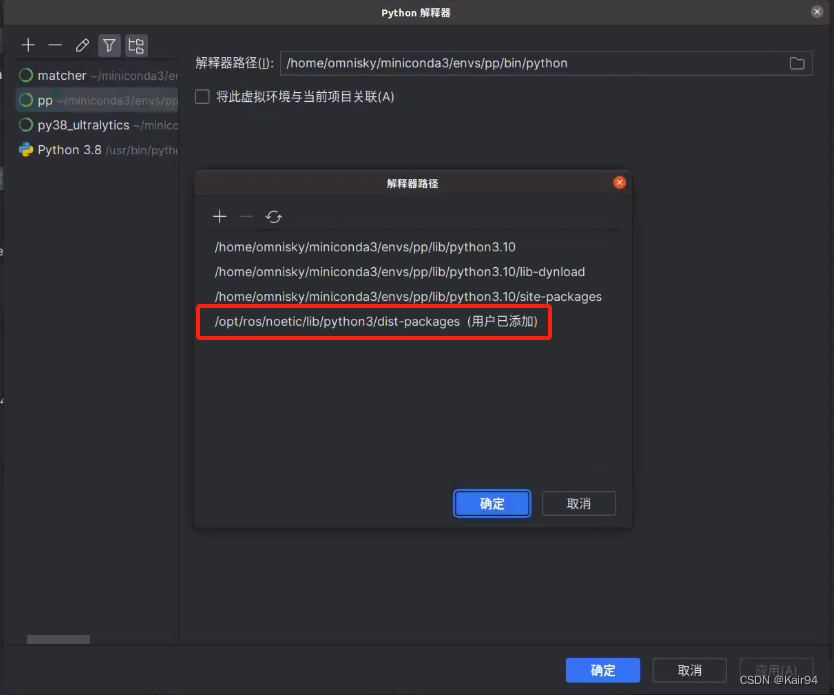
pycharm中导入rospy（ModuleNotFoundError: No module named ‘rospy‘）
1. ubuntu安装对应版本ros
ubuntu20.04可参考：
https://wiki.ros.org/cn/noetic/Installation/Ubuntuhttps://zhuanlan.zhihu.com/p/515361781
2. 安装python3-roslib
sudo apt-get install python3-roslib3.在conda环境中安装rospy
pip install rospkg
pip in…
pycharm调试bash启动的python项目（远程开发同理）
pycharm调试bash启动的python项目（远程开发同理）
步骤 打开运行/调试配置 选择Python 调试服务器 参考打开的页面，在需要debug的虚拟环境中安装依赖环境：pip install pydevd-pycharm~241.14494.158。端口号可以手动指定&…
探索鸿蒙开发：鸿蒙系统如何引领嵌入式技术革新
嵌入式技术已经成为现代社会不可或缺的一部分。而在这个领域，华为凭借其自主研发的鸿蒙操作系统，正悄然引领着一场技术革新的浪潮。本文将探讨鸿蒙开发的特点、优势以及其对嵌入式技术发展的深远影响。
鸿蒙操作系统的特点
鸿蒙，作为华为推…
pytorch基础: torch.unbind()
1. torch.unbind 作用 说明：移除指定维后，返回一个元组，包含了沿着指定维切片后的各个切片。 参数： tensor(Tensor) – 输入张量dim(int) – 删除的维度
2. 案例
案例1 x torch.rand(1,80,3,360,360)y x.unbind(dim2)print(&…
初学python记录：力扣1652. 拆炸弹
题目：
你有一个炸弹需要拆除，时间紧迫！你的情报员会给你一个长度为 n 的 循环 数组 code 以及一个密钥 k 。
为了获得正确的密码，你需要替换掉每一个数字。所有数字会 同时 被替换。
如果 k > 0 ，将第 i 个数字用…
Java中的异常处理机制
Java中的异常处理机制主要通过try、catch和finally三个关键字来实现。以下是Java异常处理机制的工作原理和正确处理异常的一些基本步骤： ## 异常处理机制的工作原理 1. **try**：包围可能抛出异常的代码块。
2. **catch**：捕获并处理特定类型…
Python | Leetcode Python题解之第70题爬楼梯
题目： 题解：
class Solution:def climbStairs(self, n: int) -> int:a, b 1, 1for _ in range(n - 1):a, b b, a breturn b
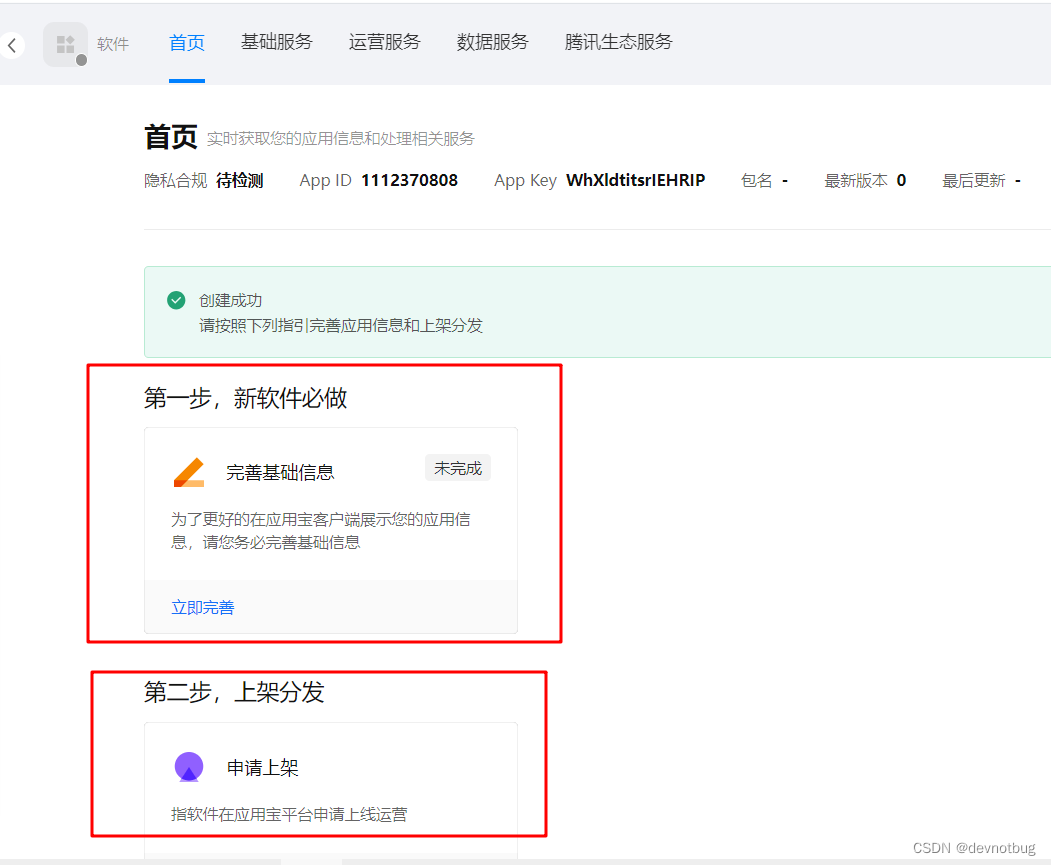
前端 Android App 上架详细流程 （Android App）
1、准备上架所需要的材料
先在需要上架的官方网站注册账号。提前把手机号，名字，身份证等等材料准备好，完成开发者实名认证；软著是必要的，提前准备好，软著申请时间比较长大概需要1-2周时间才能下来…
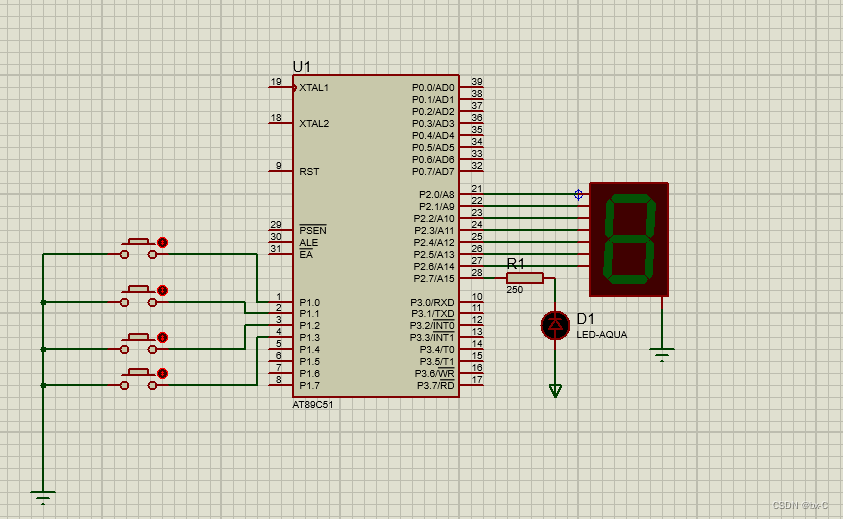
QX-mini51单片机学习-----（3）流水灯
目录
1宏定义
2函数的定义
3延时函数
4标准库函数中的循环移位函数
5循环移位函数与左移和右移运算符的区别
6实例
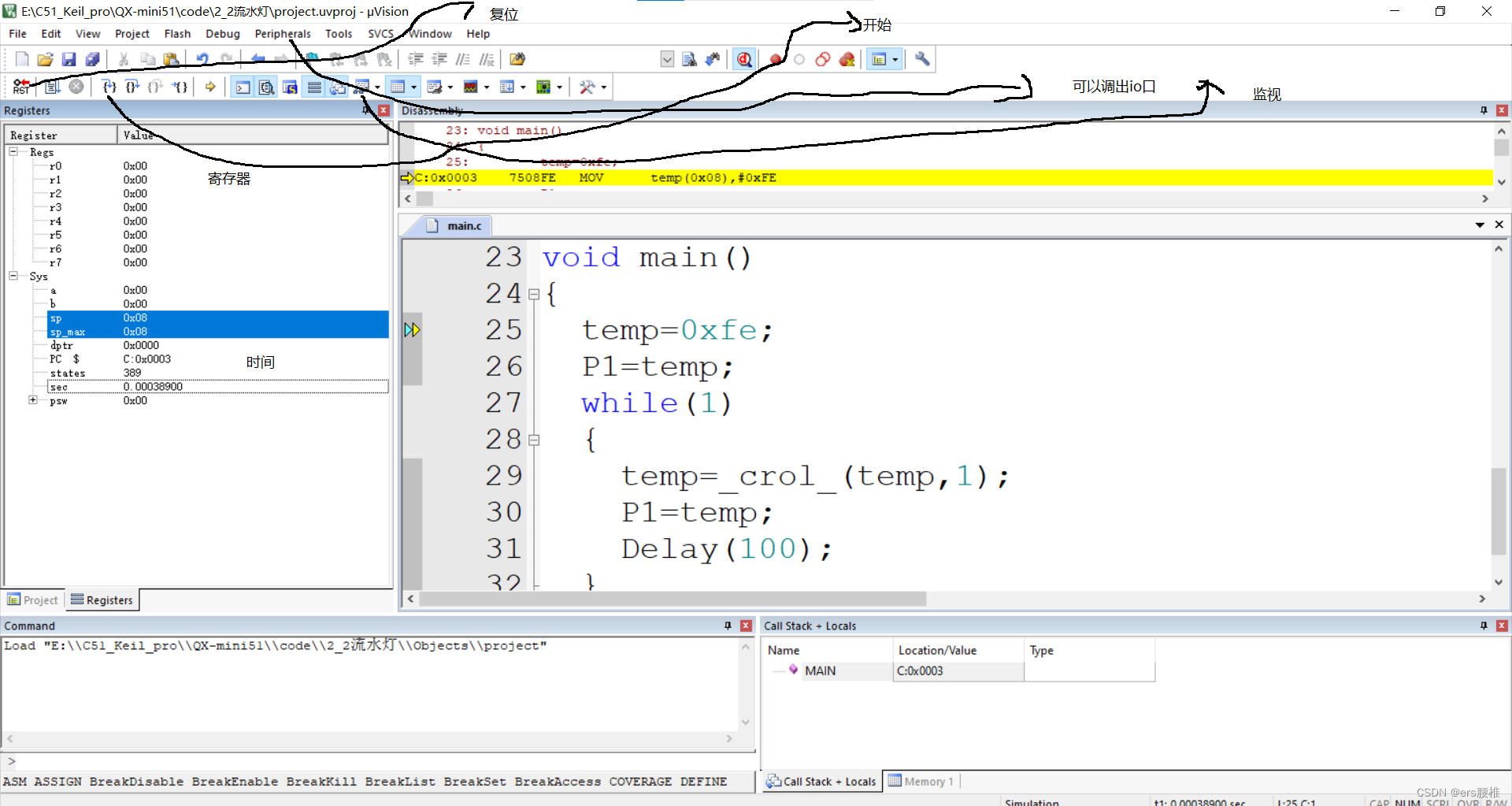
7keil中DeBug的用法
1宏定义
是预处理语句不需要分号
#define uchar unsigned char//此时uchar代替unsigned char
typedef是关键字
后面是接分号…
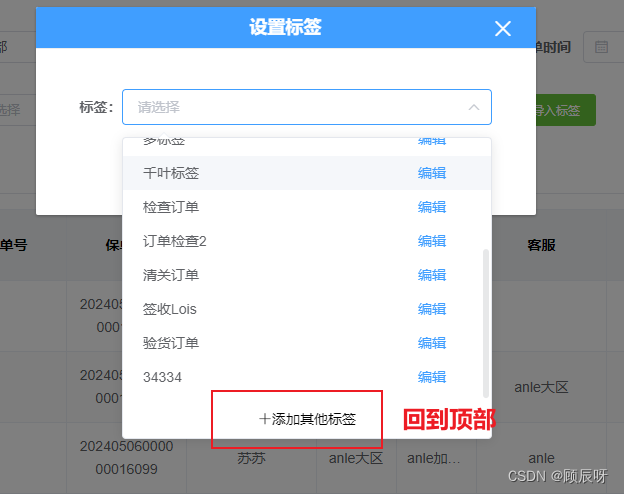
el-select 点击按钮滚动到选择框顶部
主要代码是在visibleChange 在这个 popper 里面找到 .el-select-dropdown__list let popper ref.$refs.popper const ref this.$refs.select let dom popper.querySelector(.el-select-dropdown__list) setTimeout(() > { dom.scrollIntoView() }, 800) <templat…
![[极客大挑战 2019]PHP](https://img-blog.csdnimg.cn/direct/53ac43f480bc427ab4cb6f8c9b339d31.png)
[极客大挑战 2019]PHP
1.通过目录扫描找到它的备份文件，这里的备份文件是它的源码。 2.源码当中涉及到的关键点就是魔术函数以及序列化与反序列化。
我们提交的select参数会被进行反序列化，我们要构造符合输出flag条件的序列化数据。
但是，这里要注意的就是我们提…
【Proteus】LED呼吸灯 直流电机调速
1.LED呼吸灯 #include <REGX51.H>
sbit LEDP2^0;
void delay(unsigned int t)
{while(t--);
}
void main()
{unsigned char time,i;while(1){for(time0;time<100;time){for(i0;i<20;i){LED0;delay(time);LED1;delay(100-time);}}for(time100;time>0;time--){fo…
Windows端之Python3.9及以上高版本工程打包得到的exe逆向工程解包得到pyc文件进而得到py文件的流程实现
参考来自
【python逆向 pyc反编译】python逆向全版本通杀_python反编译pyc-CSDN博客https://blog.csdn.net/zjjcxy_long/article/details/127346296Pyinstaller打包的exe之一键反编译py脚本与防反编译_pyinstaller防止反编译-CSDN博客https://blog.csdn.net/as604049322/artic…
大模型微调实战之强化学习 贝尔曼方程及价值函数（五）
大模型微调实战之强化学习 贝尔曼方程及价值函数（五）
现在， 看一下状态-动作值函数的示意图： 这个图表示假设首先采取一些行动(a)。因此，由于动作（a），代理可能会被环境转换到这些状…
推荐文章
- Spring Boot 分片上传文件
- VsCode修改侧边栏字体大小——用缩放的方法
- 旅行季《乡村振兴战略下传统村落文化旅游设计》许少辉八一著作想象和世界一样宽广
- 软考-高级-系统架构设计师教程（清华第2版）【第2章 计算机系统基础知识-思维导图】
- #渗透测试#SRC漏洞挖掘# 操作系统-Linux系统基础02之Openssl、软连接与硬连接、用户账号数据库
- （11）Python引领金融前沿：投资组合优化实战案例
- (12)Hive调优——count distinct去重优化
- (15)微信自动化测试-针对微信主窗体的行为控制
- （24）(24.2) Minim OSD快速安装指南（一）
- (3)、SpringCache源码分析
- （java）进程和线程的联系和区别 。Java如何进行多线程编程？Thread 类及常见方法。
- （JavaEE）（多线程案例）线程池 （简单介绍了工厂模式）（含经典面试题ThreadPoolExector构造方法）