一. 频谱图与梅尔谱图的介绍
频谱图:频谱图可以理解为一堆垂直堆叠在一起的快速傅里叶变换结果。
1.1 信号
在进入频谱图模块之前,首先我们需要了解信号是什么。
信号就是某一特定量随时间变化,对于音频来说,这个特定的变化量就是气压。我们采集到的信号叫做波形,他可以通过计算机来描述出来(如下图):
横轴为时间,纵轴为振幅。

现在我们得到了一个可以处理的语音信号数字表示,我们需要使用傅立叶变换来对这个波形做进一步处理。
1.2 傅立叶变换
傅立叶变换双语讲解链接
傅立叶变换是将信号从时域转为频域的强大利器。对于我们上面得到的波形信号,该信号由多个单频声波组成,当我们随着时间对信号进行采样时,我们仅仅能够捕获到最终叠加后的振幅(amplitude)。但是傅立叶变换可以帮助我们将其分解为多个频率和频率对应的振幅。最终得到的数据称为频谱。具体变化如下图所示:

1.3 快速傅立叶变换与频谱图
在得知什么是傅立叶变换后,我们引入了快速傅立叶变换(FFT),它们在数学上达到的效果是相同的,但是快速傅立叶变换将时间复杂度降低为nlogn。所以我们在实际操作中一般使用FFT(注意FFT一般要求输入数据的长度是2的幂次方)。
我们对1.1中得到的波形做快速傅立叶变换,得到下面的频谱图:

可以看到频谱的横坐标为频率,纵坐标为振幅。
But,我们忽略了一个很重要的点,那就是在上面的分析过程中,我们假设信号只是由多个单一的周期性信号组成的,但是在实际生活中,应该还掺杂着大量的非周期信号!这种信号在时间-振幅图上,显示为无规律的波形图案。
我们用简单的加法就可以得知,规则信号+不规则信号=不规则信号,因此我们实际处理的大部分音频是不规则信号。
好消息是我们仍然可以使用快速傅立叶变换来处理这些不规则信号。
怎么处理呢?好问题!
1.3.1 整体机理简单解释
首先我们要明确的是,傅立叶变换适合处理周期性的规则数据,那么我们如何将不规则的数据转换为规则数据呢?答案可能在你学微积分的时候就可以得到——那就是切分。我们将不规则的数据按照特定大小(也就是窗口)进行切分,得到较小的片段,这样的小片段更适合进行傅立叶变换。最后我们将得到每个小片段的频谱图。
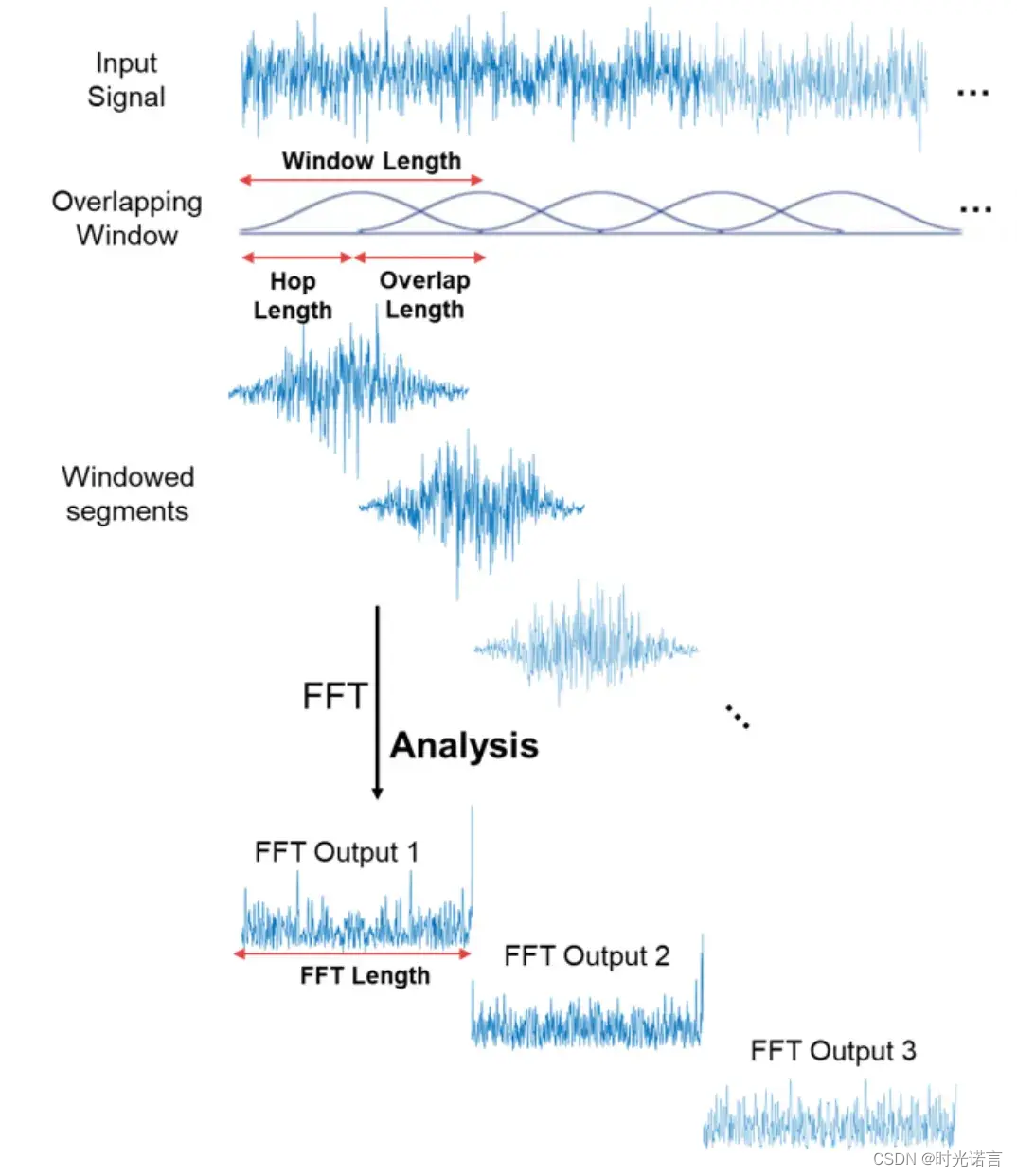
整体流程如下图所示:
1.3.2 窗函数的应用
上图展示了“Window Length”(窗长)和“Hop Length”(跳跃长度),以及窗函数的形状。窗长定义了每次FFT分析所考虑的信号长度,而跳跃长度是指每次窗口移动的时间间隔。通常,窗口之间会有一定的重叠,称为“Overlap Length”(重叠长度)。
可以看到,两个窗口会有重叠的部分,这称为窗口重叠,窗口重叠可以减少频谱的泄露,原因如下:
- 窗口效应:在对音频信号进行窗函数处理时,窗函数的边缘通常会对信号进行衰减。这会导致窗口两端的信号部分丢失信息,尤其是当信号的频率成分在窗口的边界处变化较大时。
- 连续性保持:通过使窗口之间重叠,可以保证每个信号的部分至少在两个或多个窗口中被分析,从而减少由于窗口效应导致的信息丢失和频谱泄露。
通过使用窗口函数,我们成功地将原始信号分割成多个重叠的段落,并对每个段落应用窗函数,得到多个窗口化的信号段。
1.3.3 快速傅立叶变换(FFT)分析
即对每个窗口化的信号段进行FFT分析。FFT将这些时域信号转换成频域信号,输出频率成分和它们的幅度。我们上述在做的(多个窗口进行傅立叶变换),也被称为短时傅里叶变换(short-time Fourier transform,STFT)。
我们将得到的小的窗口,通过梅尔滤波器组,这些滤波器按照梅尔尺度均匀分布,并且每个滤波器覆盖特定的频率范围。
1.3.4 后续计算
计算每个滤波器的能量:
对于每个梅尔滤波器,计算它覆盖的频率带内所有频率成分的能量总和。这通常是通过将滤波器的响应与每个窗口的频谱进行点乘并求和来完成的。
取对数:
为了更贴合人耳对声音强度的感知,在计算出每个滤波器的能量后,通常会对这些能量值取对数。这一步增强了动态范围,并且使得频谱的表示更适合后续的音频处理和分析任务。
完成上述操作后,只需要绘制出梅尔频谱图即可
1.3.5 梅尔频谱完整代码示例
#创建一个由两个正弦波组成的简单合成信号,一个频率为 300 Hz,另一个频率为 600 Hz。
fs = 8000 # Sampling frequency
duration = 1.0 # seconds
t = np.linspace(0, duration, int(fs * duration), endpoint=False)
signal = 0.5 * np.sin(2 * np.pi * 300 * t) + 0.5 * np.sin(2 * np.pi * 600 * t)#执行短时傅立叶变换(STFT)
frequencies, times, Zxx = stft(signal, fs=fs, window='hann', nperseg=256, noverlap=128)#创建梅尔过滤器并应用,即使用 librosa 创建梅尔滤波器组并将其应用于从 STFT 获得的幅度谱。
n_mels = 64 #梅尔带数
mel_filters = librosa.filters.mel(sr=fs, n_fft=256, n_mels=n_mels)
mel_spectrogram = np.dot(mel_filters, np.abs(Zxx)) # Apply Mel filterbank#取对数得到 log-Mel 频谱图
log_mel_spectrogram = np.log(mel_spectrogram + 1e-9) # Add a small number to avoid log(0)#绘制信号和 Log-Mel 频谱图
plt.figure(figsize=(12, 8))
# 绘制原本信号
plt.subplot(2, 1, 1)
plt.title("Original Signal")
plt.plot(t * 1000, signal) # Ensure t is correctly sized
plt.xlabel("Time (ms)")
plt.ylabel("Amplitude")# 绘制梅尔谱图
plt.subplot(2, 1, 2)
plt.title("Log-Mel Spectrogram")
plt.imshow(log_mel_spectrogram, aspect='auto', origin='lower', extent=[0, duration, 0, n_mels])
plt.xlabel("Time (s)")
plt.ylabel("Mel filter index")
plt.colorbar(label="Log-Magnitude")plt.tight_layout()
plt.show()
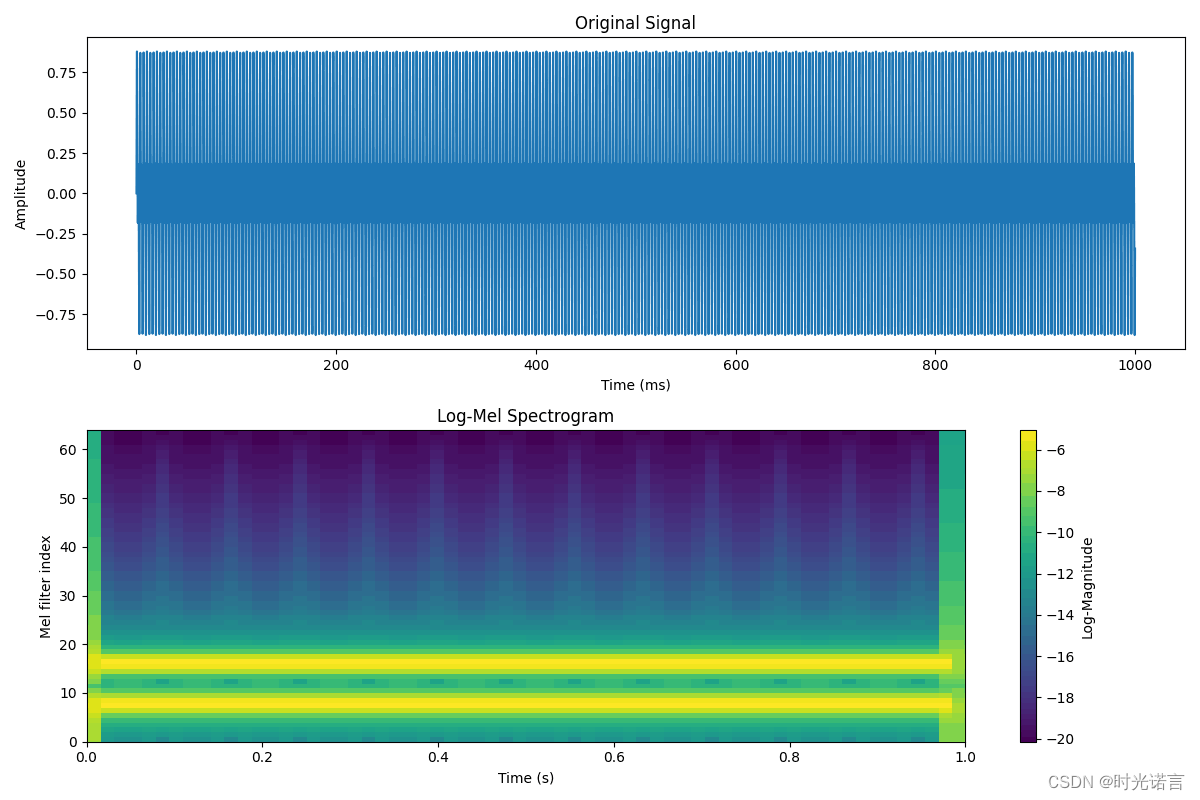
最终生成的梅尔频谱如下所示:
二. Learn2Sing 2.0歌声转换算法详解
2.1 引入
AIGC席卷下, 语音合成, 语音转换一直是音频技术的关键核心技术。 语音合成的关键是学会目标人的音色, 并迁移到源目标上。 随着元宇宙的爆火, 虚拟人逐渐走到了荧幕前, 语音合成也从音色转换升级至目标人的音色克隆。 **即给定足够时长的目标人语音, 即可通过文本的方式生成用户需要的音频片段。**然而仅仅让虚拟人说话是不够的, 歌声是一个很好表现自己的方式, 歌声转唱就是典型的应用案例。 随着“ AI孙燕姿” 的成功出圈, 让用户可以链接粉丝和偶像产生互动感, 具有很强娱乐性, 除此之外, 歌声转唱可以为每个人提供个性化的音乐体验, 用户通过录制简单的一段说话音频, 就可以定制属于自己独特音色的歌手, 让不擅长唱歌的用户完成歌曲的演唱。 这就是:Singing Voice Conversion。
歌声转换( Singing voice conversion) 旨在保证歌唱内容的同时, 将音色从source speaker转换到 target speaker, 这将为音乐行业带来革命性的变化。 歌声转唱具有很强的娱乐性, 可以使目标歌手无需重新录制歌曲, 不仅能够节省大量的时间和金钱, 还能为艺术创作开辟新的艺术道路, 同时可以让每一个用户都能实现自己独特的音色唱歌, 商业前景和市场巨大。
2.2 过去研究的不足
2.2.1 依赖大量标识数据
最早的歌声生成模型是依靠大量已经标记的声音数据,即由专业歌手录制并标记的歌唱语料库,这需要使用 MusicXML 或 MIDI 文件来训练模型SVS 任务。**But,要知道我们最终的目的是在没有相关歌声数据的情况下也能为每个用户创建自己的歌声。**所以我们不应依靠大量标记好的数据。
2.2.2 Learn2Sing 1.0中出现的问题
Learn2Sing 1.0是作者之前尝试过的一个版本,是一种歌声合成模型。虽然Learn2Sing 1.0一定程度上减少了对参考音频的依赖,但是仍然存在诸多问题:
- 音高预测的不准确:独立的基频(F0)预测模型由于训练数据有限,可能导致音高曲线不准确,从而影响最终声音的自然度和表现力。
- 推理效率低:基于自回归解码器的方法需要逐帧预测梅尔频谱图,这使得推理过程变得缓慢。
- 依赖参考音频:尽管进行了一些优化,但系统在一定程度上仍然需要参考音频,这限制了其在没有足够参考数据时的应用,尤其是在尝试合成新歌或高度表现力的歌声时。
2.3 Learn2Sing 2.0的破冰
长话短说,我们直接看Learn2Sing 2.0的整体机理:
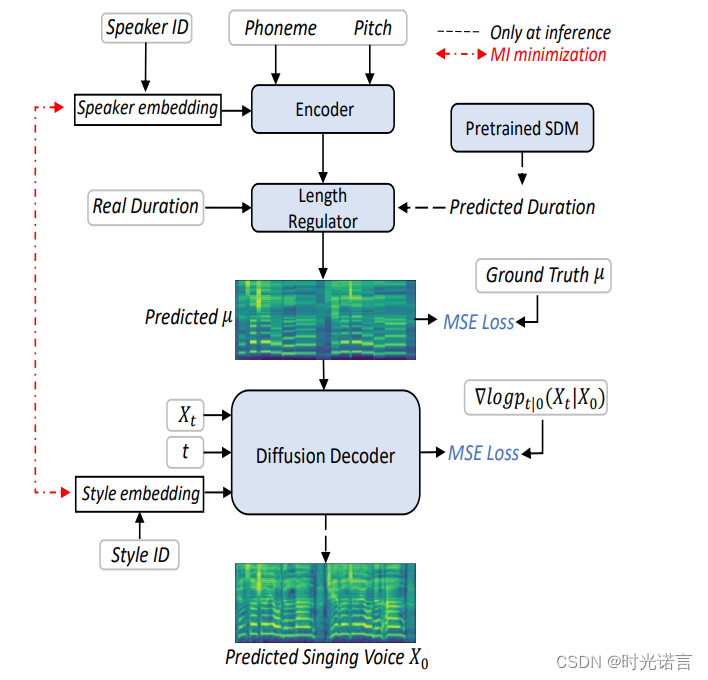
Learn2Sing 2.0的工作原理是通过两个主要阶段来合成歌声,分别是生成中间表示和基于这些表示的最终梅尔频谱图的恢复。
生成中间表示:
- 输入:该阶段接收的输入包括音素序列(phone sequence)、音高(pitch)和发言人信息(speaker information)。音素序列表示了语音的基本语音单位,音高提供了每个音素的音高信息,而发言人信息则允许模型捕捉到特定发言人的声音特征。
- 处理:首先,根据输入数据生成一个梅尔频谱图的平均值。这个平均化的过程发生在音素级别,即将与每个音素相关联的梅尔频谱图区域求平均,以形成一个更稳定和典型的表示形式。
- 上采样:生成的特征需要与原始音频的时间分辨率对齐。因此,这些特征将被上采样,以与平均梅尔频谱图对齐,为下一阶段的处理做准备。
最终梅尔频谱图的恢复:
- 输入:这一阶段的输入是上一步生成的中间表示,加上额外的风格信息。这些风格信息可以是关于发言人是在说话还是在唱歌的信息,有助于调整最终输出以更好地符合目标风格。
- 处理:使用基于扩散概率模型(DPM)的解码器来处理这些输入,逐步恢复和细化最终的梅尔频谱图。扩散概率模型(如GradTTS)是一种生成模型,能够处理含噪声的数据,并逐步去除噪声,恢复出清晰的数据表示。
2.3.1 使用到的扩散模型DPM
DPM是一种强大的建模工具,已被应用于语音合成和歌声合成(SVS)任务。
需要明确的是,DPM包含两个过程:前向扩散和逆向扩散(其实大多数扩散模型都有这两个过程)。前向扩散通过逐渐增加噪声来从真实数据获得一个可追踪的先验分布;逆向扩散则尝试还原出真实数据,通过去除噪声。
Song等人提出了一个统一的基于分数的DPM框架,然后将其应用于Grad-TTS的语音合成领域。也就是说,DPM是Grad-TTS框架的核心所在。
- 在Grad-TTS系统中,DPM的两个扩散过程被具体化为满足特定随机微分方程(SDE)的形式。
- Grad-TTS不直接解逆向时间的SDE,而是使用一个普通微分方程(ODE)来进行逆过程的计算。
- 通过估计梅尔频谱图的对数密度的梯度,Grad-TTS能够从文本预测出梅尔频谱图,然后逐步重建目标梅尔频谱图。
具体公式如下:
首先是前向扩散的过程:
d X t = 1 2 Σ − 1 ( μ − X t ) β t d t + β t d W t , t ∈ [ 0 , 1 ] d X_{t}=\frac{1}{2} \Sigma^{-1}\left(\mu-X_{t}\right) \beta_{t} d t+\sqrt{\beta_{t}} d W_{t}, t \in[0,1] dXt=21Σ−1(μ−Xt)βtdt+βtdWt,t∈[0,1]
- Xt是时间t的数据状态。
- μ 是数据的均值(通常是数据的起始状态或期望状态)。
- βt是噪声程度,随时间变化的调度参数。
- dWt是标准布朗运动(白噪声源)。
- 此方程逐渐增加数据的噪声水平,使数据从初始状态X0随时间演变到更加随机的状态。
然后是逆向扩散过程:
d X t = ( 1 2 Σ − 1 ( μ − X t ) − ∇ log p t ( X t ∣ X 0 ) ) β t d t + β t d W ~ t , t ∈ [ 0 , 1 ] \begin{array}{l}d X_{t}=\left(\frac{1}{2} \Sigma^{-1}\left(\mu-X_{t}\right)-\nabla \log p_{t}\left(X_{t} \mid X_{0}\right)\right) \beta_{t} d t +\sqrt{\beta_{t}} d \widetilde{W}_{t}, \quad t \in[0,1]\end{array} dXt=(21Σ−1(μ−Xt)−∇logpt(Xt∣X0))βtdt+βtdW t,t∈[0,1]
- 最后一项 β t d W ~ t \sqrt{\beta_{t}} d \widetilde{W}_{t} βtdW t表示在逆向过程中,噪声被逐渐移除
利用常微分方程(ODE)来代替直接解决逆向时间的 SDE:
d X t = 1 2 ( μ − X t − s θ ( X t , μ , t ) ) β t d t d X_{t}=\frac{1}{2}\left(\mu-X_{t}-s_{\theta}\left(X_{t}, \mu, t\right)\right) \beta_{t} d t dXt=21(μ−Xt−sθ(Xt,μ,t))βtdt
- s θ ( X t , μ , t ) s_{\theta}\left(X_{t}, \mu, t\right) sθ(Xt,μ,t)是一个评分函数,用于估计对数概率密度的梯度。这个函数是可学习的,它在推断阶段帮助逐步修正噪声数据 Xt ,使之逼近目标数据 μ。
- βt控制着噪声的减少速度。
- 通过调整评分函数和噪声调度,Grad-TTS 在推断阶段能够逐步从噪声状态重构目标梅尔频谱图。
我们有必要在这里梳理清楚模型的两个关键时期——训练阶段与推断阶段
还是看上面那张图,在训练阶段,被更新参数的模块包括:
- 编码器Encoder:
输入包括Speaker ID、Phoneme(音素)、和Pitch(音高)。
这些输入通过编码器处理,得到声音的中间表示。这一步涉及到学习如何根据不 同的发音和音调来调整声音的特性。 - 长度调节器(Length Regulator):
使用预测的持续时间(Predicted Duration)调整音节的长度,以符合真实的持续时间(Real Duration),另外要注意的是,Length Regulator起到了上采样的作用。 - 预测的梅尔频谱μ:
从编码器输出得到预测的梅尔频谱图μ,并与真实的梅尔频谱图(Ground Truth μ)比较,计算均方误差(MSE Loss)。 - 扩散解码器(Diffusion Decoder):
使用噪声时间t和扩散过程来从预测的梅尔频谱图μ生成噪声梅尔频谱Xt,再反向通过扩散过程逼近真实的梅尔频谱图X0,同样使用MSE Loss作为训练损失。
而在推断阶段,使用到的模块有(此时各模块参数冻结):
- 使用预训练的评分模型 SDM:
在推断阶段,预训练的评分模型(SDM)(这是在训练阶段训练好的)用于帮助精确调节生成的梅尔频谱,尽可能逼近真实的梅尔频谱图。 - 最小化互信息(MI minimization):
这通常在推断阶段进行,旨在减少不同模式间的相互信息,帮助模型更好地泛化,提高输出的多样性和自然性。 - 样式嵌入(Style Embedding)和样式ID(Style ID):
这些在推断过程中被用来调整输出以符合特定的声音风格和特性。 - 生成预测的歌声X0:
最终输出是预测的歌声梅尔频谱图 X0,这是通过逐步从带噪声的梅尔频谱Xt进行细化得到的。
总之,训练部分涉及构建和优化模型,使其能够从给定的输入生成准确的输出。推断部分则是实际应用训练好的模型,以生成符合用户期望的高质量声音输出。
2.3.2 Proposed Learn2Sing 2.0 Model
OK,我们知道了整体的流程,现在我们来把细节整理清楚。以下是几个比价关键的细节:
- Encoder生成的是一个中间状态的梅尔谱图,即音素级平均梅尔频谱图μ。它不参与生成speaker音高即pitch特征!
- speaker的音高特征是在扩散模型中主键恢复的。
- 在同一音素内不存在不同的发音或唱歌风格,比如过载、颤音、准备期或音调波动,因为所有帧内的μ都是相同的。
- 在文本到语音(TTS)系统中,经常会出现系统混淆speaker embedding和style embedding的情况。说话者嵌入(speaker embedding)旨在捕捉与特定说话者相关的特征,如音色和发音习惯;而风格嵌入(style embedding)则捕捉发音的风格,如情感表达、语调变化和语速。Learn2Sing 2.0 使用了vCLUB来解决这个问题(也就是互信息模块),其损失函数如下所示:
L m i = 1 N 2 ∑ i = 1 N ∑ j = 1 N [ log q θ ( s t y i ∣ s p k i ) − log q θ ( s t y j ∣ s p k i ) ] \mathcal{L}_{\mathrm{mi}}=\frac{1}{N^{2}} \sum_{i=1}^{N} \sum_{j=1}^{N}\left[\log q_{\theta}\left(\boldsymbol{s t} \boldsymbol{y}_{i} \mid \boldsymbol{s p} \boldsymbol{k}_{i}\right)-\log q_{\theta}\left(\boldsymbol{s t} \boldsymbol{y}_{j} \mid \boldsymbol{s p} \boldsymbol{k}_{i}\right)\right] Lmi=N21i=1∑Nj=1∑N[logqθ(styi∣spki)−logqθ(styj∣spki)] - 第一项 log q θ ( s t y i ∣ s p k i ) \log q_{\theta}\left(\boldsymbol{s t y}_{i} \mid \boldsymbol{s p k}_{i}\right) logqθ(styi∣spki)是在给定第i个人的spk嵌入下,预测为i的风格的概率。
- 第二项 log q θ ( s t y j ∣ s p k i ) \log q_{\theta}\left(\boldsymbol{s t y}_{j} \mid \boldsymbol{s p k}_{i}\right) logqθ(styj∣spki)是在给定第i个人的spk嵌入下,预测为j的风格的概率。
这两项的差值如果越大,意味着qθ误判的概率越大(即将spki误判为styi的概率较大),这显然不是我们所期待的,所以我们选择最小化这个损失。
其中qθ成为可学习的参数,它的更新方式是对数似然更新(如下所示,其实和上面这个损失函数就是照应的):
L ( θ ) = 1 N ∑ i = 1 N log q θ ( s t y i ∣ s p k i ) \mathcal{L}(\theta)=\frac{1}{N} \sum_{i=1}^{N} \log q_{\theta}\left(\boldsymbol{s t y}_{i} \mid \boldsymbol{s p \boldsymbol { k } _ { i }}\right) L(θ)=N1i=1∑Nlogqθ(styi∣spki)
总损失为:
L total = L μ + L diff + λ L m i \mathcal{L}_{\text {total }}=\mathcal{L}_{\mu}+\mathcal{L}_{\text {diff }}+\lambda \mathcal{L}_{m i} Ltotal =Lμ+Ldiff +λLmi
L μ \mathcal{L}_{\mu} Lμ是是预测的μ 和实际μ之间的均方误差损失, L diff \mathcal{L}_{\text {diff }} Ldiff 是扩散误差, λ L m i \lambda \mathcal{L}_{m i} λLmi就是刚才所说的互信息损失,λ是一个超参系数。
2.3.3 Fast Maximum Likelihood Sampling Scheme
在采样也就是解码阶段,该模型使用的是固定步长一阶逆SDE求解器(目的是加速采样的速度,在保证速度的同时保证质量),旨在最大化前向扩散离散采样路径的似然性。具体来说,快速采样方案首先定义了以下值:
γ s , t = exp ( − 1 2 ∫ s t β u d u ) , ϕ s , t = γ s , t 1 − γ 0 , s 2 1 − γ 0 , t 2 , ν s , t = γ 0 , s 1 − γ s , t 2 1 − γ 0 , t 2 , σ s , t 2 = ( 1 − γ 0 , s 2 ) ( 1 − γ s , t 2 ) 1 − γ 0 , t 2 , κ t , h = ν t − h , t ( 1 − γ 0 , t 2 ) γ 0 , t β t h − 1 ω t , h = ϕ t − h , t − 1 β t h + 1 + κ t , h 1 − γ 0 , t 2 − 1 2 , ( σ t , h ) 2 = σ t − h , t 2 \begin{array}{c}\gamma_{s, t}=\exp \left(-\frac{1}{2} \int_{s}^{t} \beta_{u} d u\right), \phi_{s, t}=\gamma_{s, t} \frac{1-\gamma_{0, s}^{2}}{1-\gamma_{0, t}^{2}}, \\\nu_{s, t}=\gamma_{0, s} \frac{1-\gamma_{s, t}^{2}}{1-\gamma_{0, t}^{2}}, \sigma_{s, t}^{2}=\frac{\left(1-\gamma_{0, s}^{2}\right)\left(1-\gamma_{s, t}^{2}\right)}{1-\gamma_{0, t}^{2}}, \\\kappa_{t, h}=\frac{\nu_{t-h, t}\left(1-\gamma_{0, t}^{2}\right)}{\gamma_{0, t} \beta_{t} h}-1 \\\omega_{t, h}=\frac{\phi_{t-h, t}-1}{\beta_{t} h}+\frac{1+\kappa_{t, h}}{1-\gamma_{0, t}^{2}}-\frac{1}{2},\left(\sigma_{t, h}\right)^{2}=\sigma_{t-h, t}^{2}\end{array} γs,t=exp(−21∫stβudu),ϕs,t=γs,t1−γ0,t21−γ0,s2,νs,t=γ0,s1−γ0,t21−γs,t2,σs,t2=1−γ0,t2(1−γ0,s2)(1−γs,t2),κt,h=γ0,tβthνt−h,t(1−γ0,t2)−1ωt,h=βthϕt−h,t−1+1−γ0,t21+κt,h−21,(σt,h)2=σt−h,t2
这部分定义了一系列参数和方程,这些都是在执行扩散过程的逆过程中用来计算每一步中所需的具体数值。这些数值和方程是为了最大化在正向扩散过程中离散样本路径的似然概率。

并采用以下类反向SDE求解:
X t − h = X t + β t h ( ( 1 2 + ω t , h ) ( X t − μ ) + ( 1 + κ t , h ) s θ ( X t , μ , s t y , t ) ) + σ t , h ξ t \begin{array}{r}X_{t-h}=X_{t}+\beta_{t} h\left(\left(\frac{1}{2}+\omega_{t, h}\right)\left(X_{t}-\mu\right)\right. \\\left.+\left(1+\kappa_{t, h}\right) s_{\theta}(X t, \mu, \boldsymbol{s t y}, t)\right)+\sigma_{t, h} \xi_{t}\end{array} Xt−h=Xt+βth((21+ωt,h)(Xt−μ)+(1+κt,h)sθ(Xt,μ,sty,t))+σt,hξt

2.4 效果展示
Teacher声音
Student原始声音
Student经Teacher指导后合成后的声音
好了,希望以上内容可以帮到大家,未来一起进步!码字不易,还请点赞收藏支持一下叭