数据结构——图

链接: 来源：link

1、基础知识

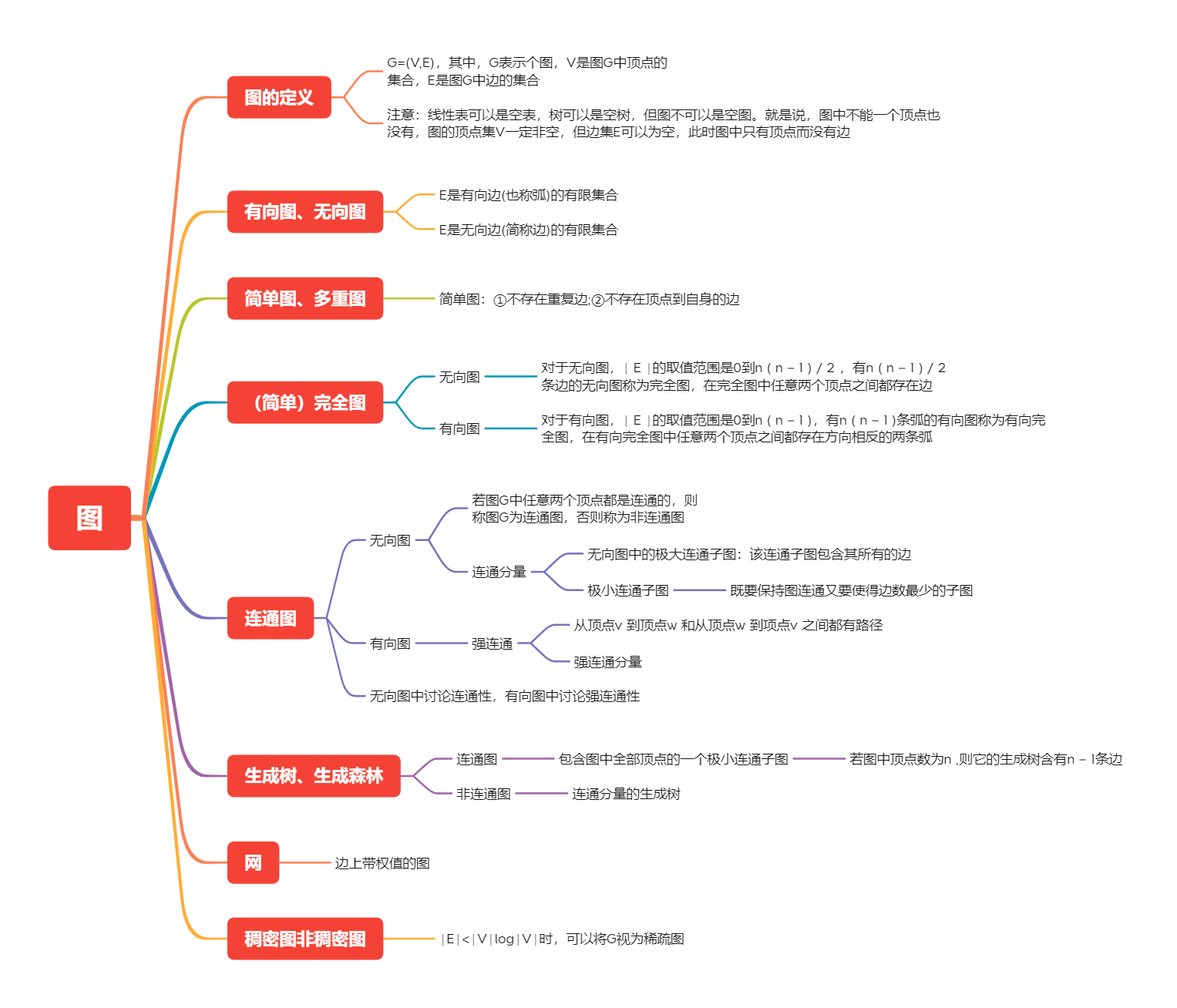
在这里插入图片描述

2、图的存储结构

1、邻接矩阵

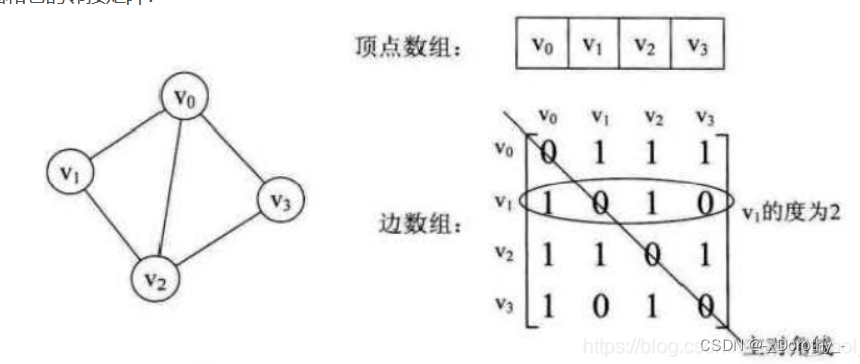
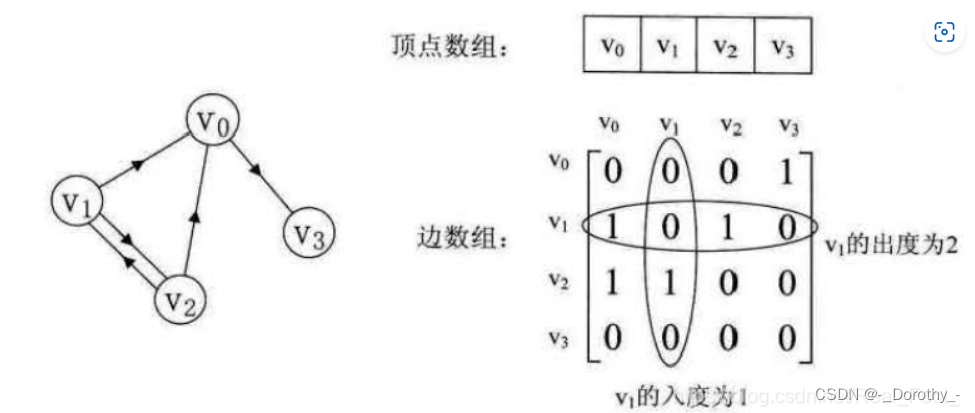
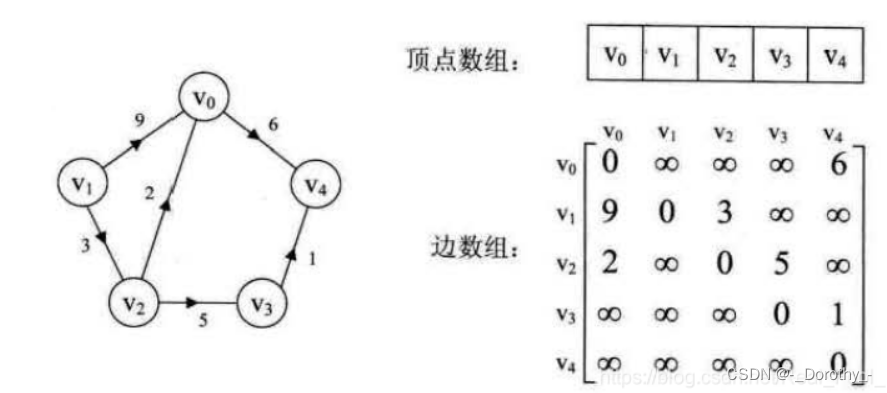
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
注意：

  • 邻接矩阵表示法的空间复杂度为O(n^2)， 其中n为图的顶点数∣V∣。
  • 用邻接矩阵法存储图，很容易确定图中任意两个顶点之间是否有边相连。但是，要确定图中有多少条边，则必须按行、按列对每个元素进行检测，所花费的时间代价很大
  • 稠密图适合使用邻接矩阵的存储表示。

2、邻接表

所谓邻接表，是指对图G中的每个顶点vi建立一个单链表, 第i个单链表中的结点表示依附于顶点vi的边(对于有向图则是以顶点vi为尾的弧)，这个单链表就称为顶点V;的边表(对于有向图则称为出边表)。边表的头指针和顶点的数据信息采用顺序存储(称为顶点表),所以在邻接表中存在两种结点:顶点表结点和边表结点
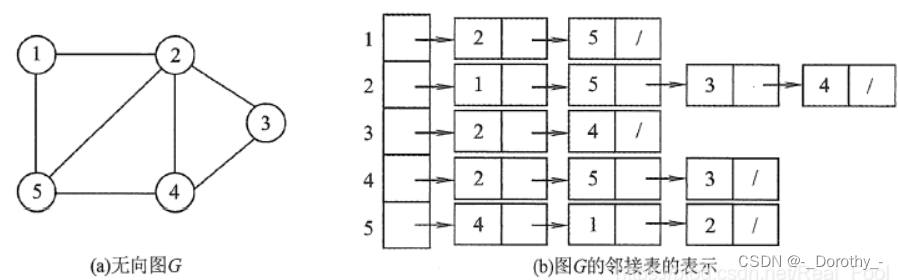
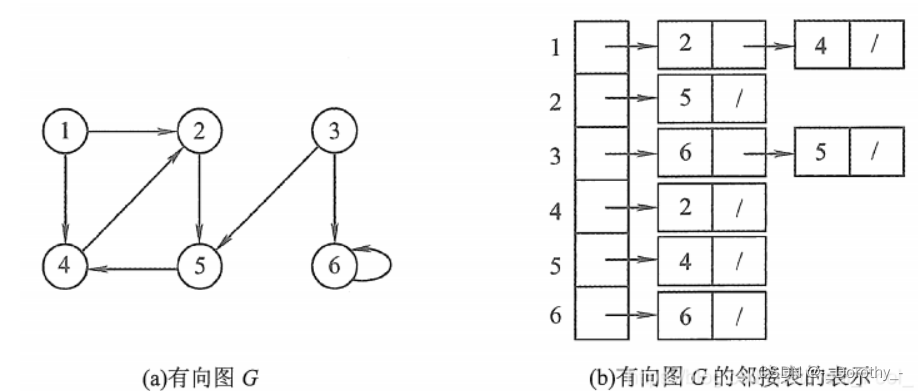
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

  • 1.若G为无向图,则所需的存储空间为O(|V | + 2|E|);若G为有向图，则所需的存储空间为O(|V| + |E|)。前者的倍数2是由于无向图中，每条边在邻接表中出现了两次
  • 2.对于稀疏图,采用邻接表表示将极大地节省存储空间。
  • 3.在邻接表中,给定顶点,能很容易地找出它的所有邻边，因为只要读取它的邻接表。在邻接矩阵中,相同的操作则需要扫描一行,花费的时间为O(n)。但是,若要确定给定的两个顶点间是否存在边,则在邻接矩阵中可以立刻查到，而在邻接表中则需要在相应结点对应的边表中查找另一点,效率较低。
  • 4.在有向图的邻接表表示中,求一个给定顶点的出度只需计算其邻接表中的结点个数;但求其颠点的入度则需要遍历全部的邻接表。因此,也有人采用逆邻接表的存储方式来加速求解给定顶点的入度。当然，这实际上与邻接表存储方式是类似的。
  • 5.图的邻接表并不唯一,因为在每 个顶点对应的单链表中,各边结点的链接次可以是任意的，它取决于建立邻接表的算法及边的 输入次序。

邻接表：适合稀疏图，空间复杂度低，但是求出度很容易、求入度要遍历所有边表
邻接矩阵：不适合稀疏图，空间复杂度O(n^2),出度是遍历第i行，入度遍历第i列

3、图的实现——邻接表

（1）无向图的实现

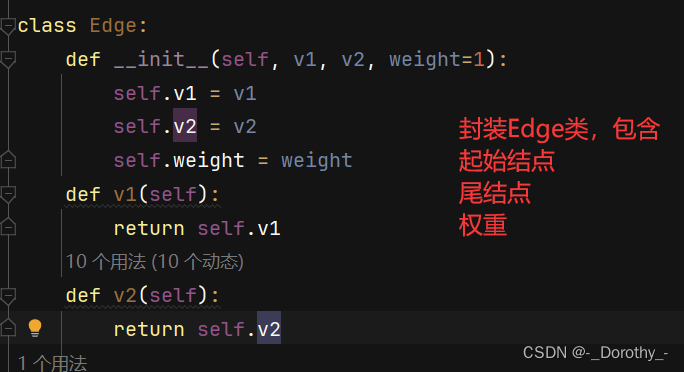
class Edge:def __init__(self, v1, v2, weight=1):self.v1 = v1self.v2 = v2self.weight = weightdef v1(self):return self.v1def v2(self):return self.v2
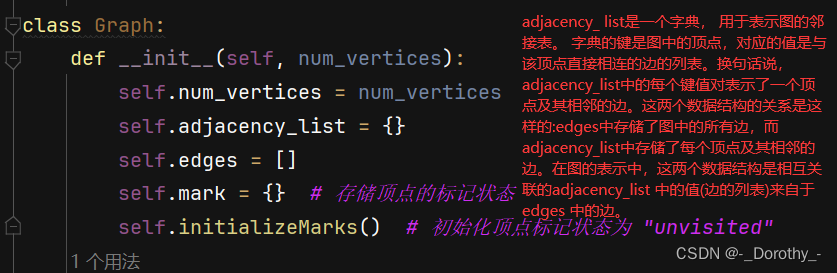
class Graph:def __init__(self, num_vertices):self.num_vertices = num_verticesself.adjacency_list = {}self.edges = []self.mark = {}  # 存储顶点的标记状态self.initializeMarks()  # 初始化顶点标记状态为 "unvisited"def initializeMarks(self):for i in range(self.num_vertices):self.mark[i] = "unvisited"def n(self):return self.num_verticesdef e(self):return len(self.edges)def first(self, v):if v in self.adjacency_list:edges = self.adjacency_list[v]return edges[0] if edges else Nonereturn Nonedef next(self, w):#边w的下一条边v1 = w.v1v2 = w.v2if v1 in self.adjacency_list:edges = self.adjacency_list[v1]index = edges.index(w)#返回w的索引值return edges[index + 1] if index + 1 < len(edges) else Nonereturn Nonedef isEdge(self, w):return w in self.edgesdef isEdgeByVertices(self, i, j):for edge in self.edges:if (edge.v1 == i and edge.v2 == j) or (edge.v1 == j and edge.v2 == i):return Truereturn Falsedef v1(self, w):return w.v1def v2(self, w):return w.v2def setEdge(self, i, j, weight):#创建边的过程中假如没有点会自动创建edge1 = Edge(i, j, weight)edge2 = Edge(j, i, weight)self.edges.append(edge1)if i not in self.adjacency_list:self.adjacency_list[i] = []if j not in self.adjacency_list:self.adjacency_list[j] = []self.adjacency_list[i].append(edge1)self.adjacency_list[j].append(edge2)def setEdgebyweight(self, w, weight):w.weight = weightdef delEdge(self, w):if w in self.edges:self.edges.remove(w)self.adjacency_list[w.v1].remove(w)self.adjacency_list[w.v2].remove(w)def delEdgebyvertex(self, i, j):for edge in self.edges:if (edge.v1 == i and edge.v2 == j) or (edge.v1 == j and edge.v2 == i):self.edges.remove(edge)self.adjacency_list[edge.v1].remove(edge)self.adjacency_list[edge.v2].remove(edge)breakdef weightbyvertex(self, i, j):for edge in self.edges:if (edge.v1 == i and edge.v2 == j) or (edge.v1 == j and edge.v2 == i):return edge.weightreturn Nonedef weight(self, w):return w.weightdef setMark(self, v, val):#用来检验是否被访问过if v in self.mark:self.mark[v] = valdef getMark(self, v):return self.mark[v]  # 默认未访问过的顶点标记为 "unvisited"

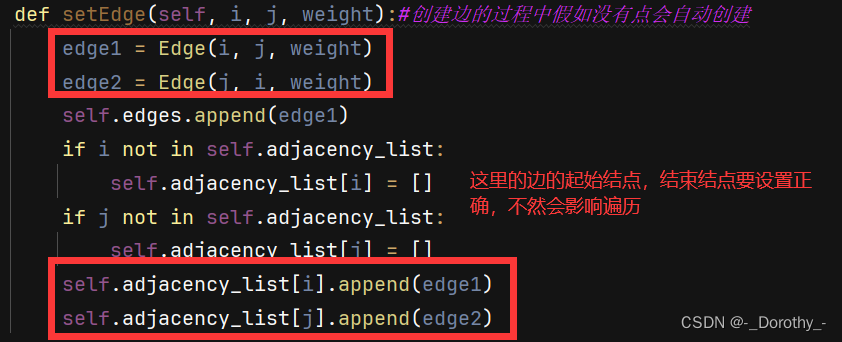
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

注意：

  • adjacency_ list是一个字典， 用于表示图的邻接表。
    字典的键是图中的顶点，对应的值是与该顶点直接相连的边的列表。换句话说，adjacency_list中的每个键值对表示了一个顶点及其相邻的边。这两个数据结构的关系是这样的:edges中存储了图中的所有边，而adjacency_list中存储了每个顶点及其相邻的边。在图的表示中，这两个数据结构是相互关联的adjacency_list
    中的值(边的列表)来自于edges 中的边。
  • setMark getMark 这两个方法提供了一种在图中附加额外信息的方法，以便在算法中进行状态跟踪或其他操作时使用

（2）实例

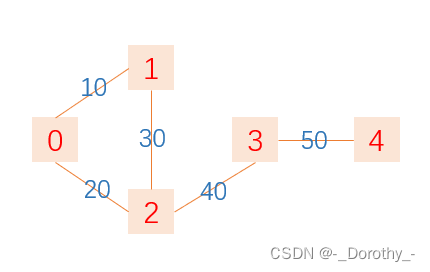
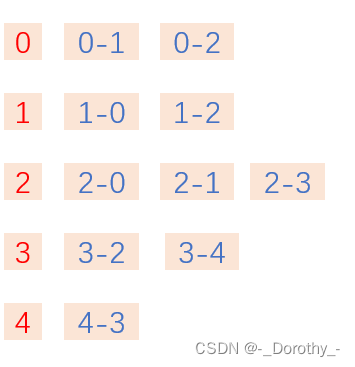
在这里插入图片描述
在这里插入图片描述

# 创建一个图实例
g = Graph(5)
# 添加顶点之间的边
g.setEdge(0, 1, 10)
g.setEdge(0, 2, 20)
g.setEdge(1, 2, 30)
g.setEdge(2, 3, 40)
g.setEdge(3, 4, 50)
# 打印图的顶点数和边数
print("Number of vertices:", g.n())
print("Number of edges:", g.e())
# 打印每个顶点的第一条边和每条边的下一条边
for v in range(g.n()):first_edge = g.first(v)if first_edge:print("First edge for vertex", v, ":", first_edge.v1, "-", first_edge.v2, "(Weight:", first_edge.weight, ")")next_edge = g.next(first_edge)while next_edge:print("Next edge for", first_edge.v1, "-", first_edge.v2, ":", next_edge.v1, "-", next_edge.v2, "(Weight:", next_edge.weight, ")")next_edge = g.next(next_edge)
# 判断是否存在某条边
print("Is edge (0, 1) in the graph?", g.isEdgeByVertices(0, 1))
print("Is edge (2, 4) in the graph?", g.isEdgeByVertices(2, 4))
# 获取边的权重
print("Weight of edge (2, 3):", g.weightbyvertex(2, 3))
# 设置顶点的标记
g.setMark(0,"visited")
print("Mark of vertex 0:", g.getMark(0))

结果

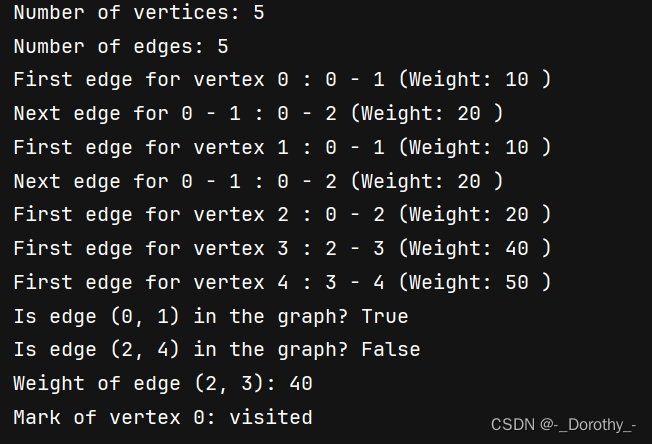
在这里插入图片描述

（3）有向图的实现

在next方法处做修改
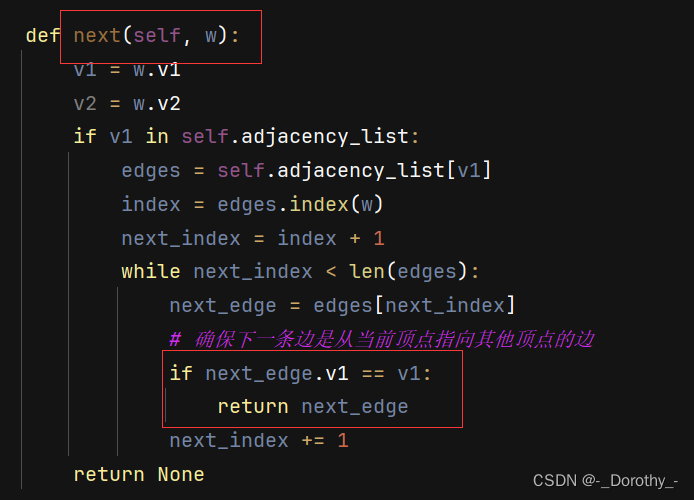
在这里插入图片描述

from graphviz import Digraphclass Graph:def __init__(self, num_vertices):self.num_vertices = num_verticesself.adjacency_list = {}self.edges = []self.mark = {}self.initializeMarks()  # 初始化顶点标记状态为 "unvisited"def initializeMarks(self):for i in range(self.num_vertices):self.mark[i] = "unvisited"def n(self):return self.num_verticesdef first(self, v):if v in self.adjacency_list:edges = self.adjacency_list[v]return edges[0] if edges else Nonereturn Nonedef next(self, w):v1 = w.v1v2 = w.v2if v1 in self.adjacency_list:edges = self.adjacency_list[v1]index = edges.index(w)next_index = index + 1while next_index < len(edges):next_edge = edges[next_index]# 确保下一条边是从当前顶点指向其他顶点的边if next_edge.v1 == v1:return next_edgenext_index += 1return Nonedef isEdge(self, w):return w in self.edgesdef setEdge(self, i, j, weight):edge = Edge(i, j, weight)self.edges.append(edge)if i not in self.adjacency_list:self.adjacency_list[i] = []self.adjacency_list[i].append(edge)def setMark(self, v, val):if v in self.mark:self.mark[v] = valdef getMark(self, v):return self.mark[v]class Edge:def __init__(self, v1, v2, weight=1):self.v1 = v1self.v2 = v2self.weight = weightdef visualize_graph(graph):dot = Digraph()for v, edges in graph.adjacency_list.items():for edge in edges:dot.node(str(edge.v1))dot.node(str(edge.v2))dot.edge(str(edge.v1), str(edge.v2), label=str(edge.weight))dot.render('directed_graph', format='png', cleanup=True)# 创建一个图实例
g = Graph(6)
# 添加顶点之间的边
g.setEdge(0, 2, 10)
g.setEdge(0, 4, 20)
g.setEdge(4, 5, 30)
g.setEdge(3, 5, 40)
g.setEdge(2, 3, 50)
g.setEdge(2, 5, 50)
g.setEdge(2, 1, 50)
g.setEdge(1, 5, 50)# 可视化有向图
visualize_graph(g)

结果
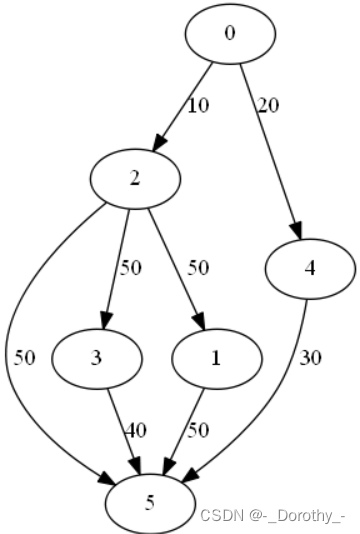
在这里插入图片描述

4、图的遍历

（1）DFS（depth first search）深度优先搜索

（类似二叉树的先序遍历）
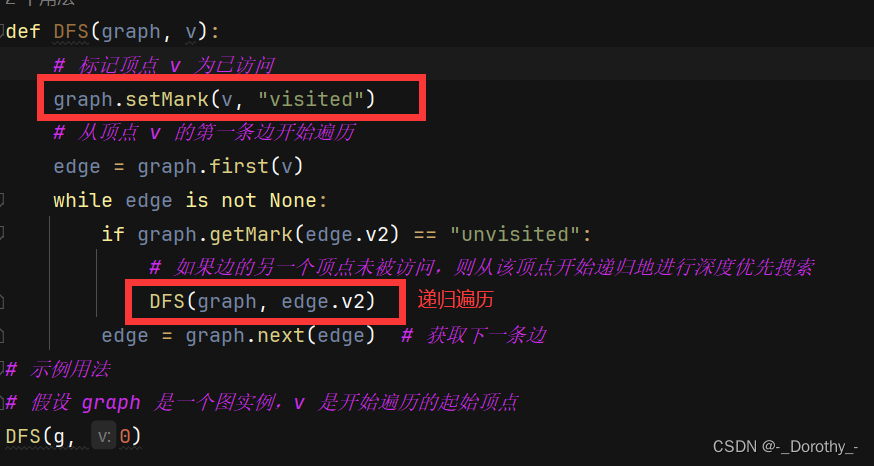
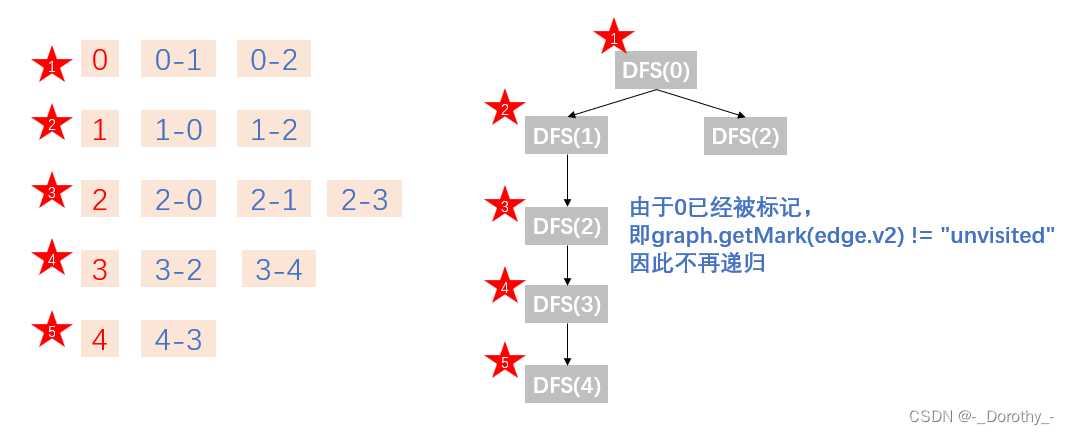
在这里插入图片描述
在这里插入图片描述
结果
在这里插入图片描述
复习二叉树的DFS先/中/后序遍历
链接: 二叉树的遍历——DFS深度优先搜索——先（根）序遍历、中序遍历、后序遍历

注意

若图不是连通图，从顶点v发起的遍历结束并不意味着图的遍历结束，如果还有v到达不了的，要在剩余的中间重新选一个

DFS生成树

# 创建一个图实例
g = Graph(6)
# 添加顶点之间的边
g.setEdge(0, 2, 10)
g.setEdge(0, 4, 20)
g.setEdge(4, 5, 30)
g.setEdge(3, 5, 40)
g.setEdge(2, 3, 50)
g.setEdge(2, 5, 50)
g.setEdge(2, 1, 50)
g.setEdge(1, 5, 50)
# 设置顶点的标记
g.setMark(0, "unvisited")  # 重置标记状态
for v in range(g.n()):if g.getMark(v) == "unvisited":root = TreeNode(v)DFS(g, v, parent=root)break
dot = Digraph()def build_tree(node, parent=None):dot.node(str(node.vertex))if parent is not None:dot.edge(str(parent.vertex), str(node.vertex))for child in node.children:build_tree(child, parent=node)build_tree(root)# 显示图形
dot.render('graph_tree', format='png', cleanup=True)

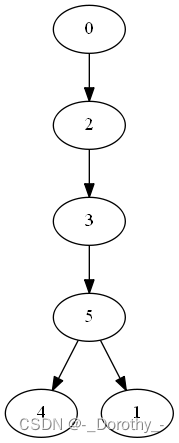
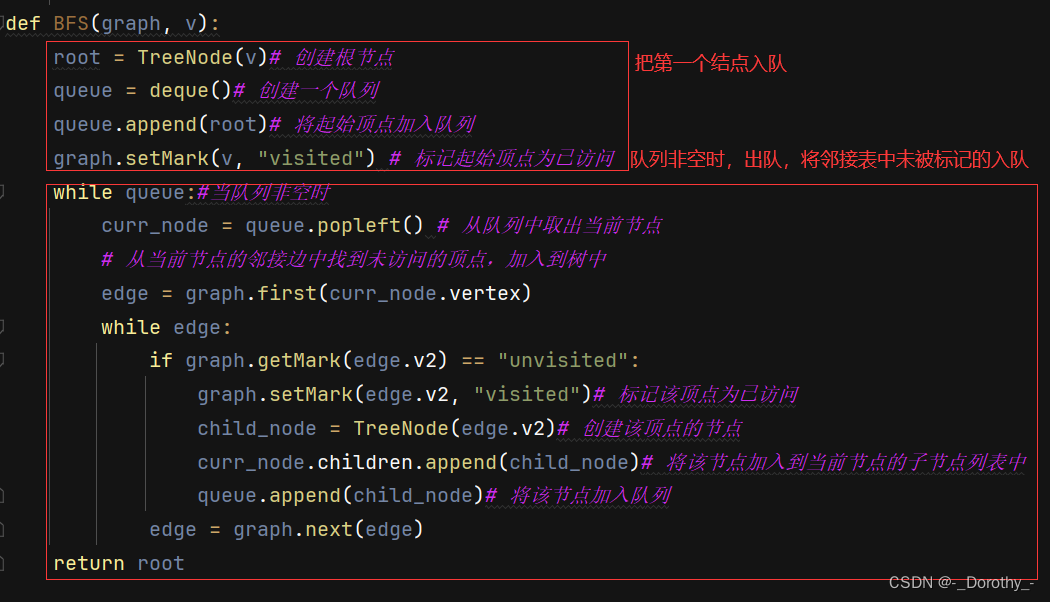
在这里插入图片描述

（2）BFS（breadth first search）广度优先搜索

如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历了。
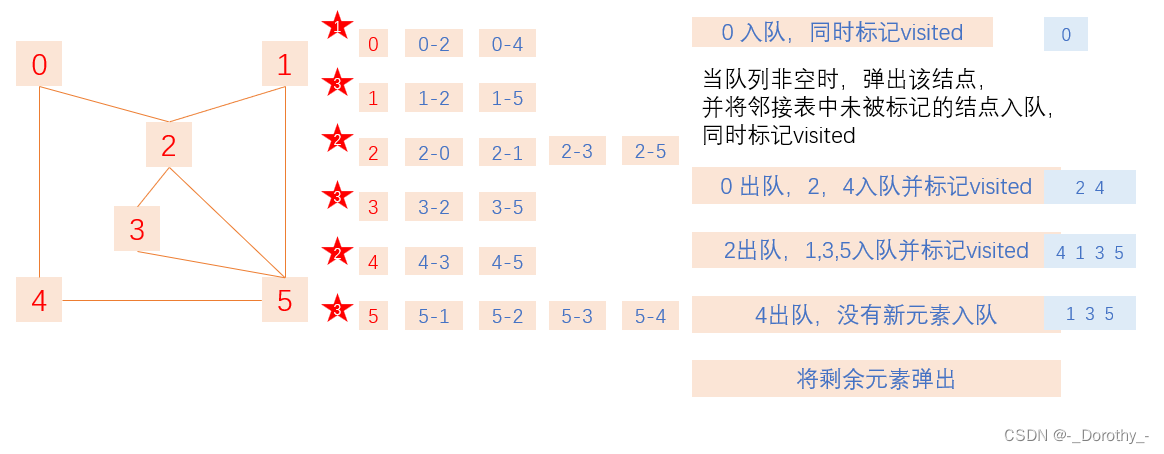
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

注意

  • pop()：这是列表方法，用于从列表的末尾删除并返回元素。如果列表为空，则会引发 IndexError。
    popleft()：这是双端队列（deque）方法，用于从队列的左侧删除并返回元素。如果队列为空，则会引发 IndexError。
    因此，主要区别在于 pop() 是列表方法，而 popleft() 是双端队列方法。如果你需要在队列的左侧执行弹出操作，你应该使用
    popleft() 方法。

BFS生成树

def visualize_bfs_tree(root):dot = Digraph()# 使用 BFS 遍历生成树，构建图形def build_tree(node, parent=None):dot.node(str(node.vertex))if parent is not None:dot.edge(str(parent.vertex), str(node.vertex))for child in node.children:build_tree(child, parent=node)build_tree(root)# 显示图形dot.render('bfs_tree', format='png', cleanup=True)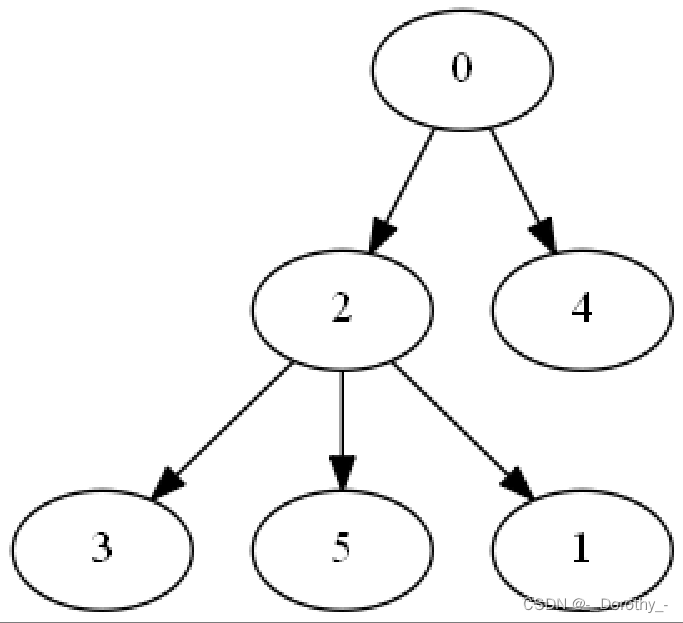

在这里插入图片描述

改进——增加外循环使其对非连通图同样适用

def BFS(graph, v):roots = []  # 存储所有连通分量的根节点while True:# 找到一个未被访问的顶点作为起始顶点start_vertex = Nonefor vertex in range(graph.n()):if graph.getMark(vertex) == "unvisited":start_vertex = vertexbreak# 如果所有顶点都已被访问，则退出循环if start_vertex is None:breakroot = TreeNode(start_vertex)  # 创建一个连通分量的根节点queue = deque()  # 创建一个队列queue.append(root)  # 将根节点加入队列graph.setMark(start_vertex, "visited")  # 标记起始顶点为已访问while queue:  # 当队列非空时curr_node = queue.popleft()  # 从队列中取出当前节点# 遍历当前节点的邻居顶点edge = graph.first(curr_node.vertex)while edge:if graph.getMark(edge.v2) == "unvisited":graph.setMark(edge.v2, "visited")  # 标记邻居顶点为已访问child_node = TreeNode(edge.v2)  # 创建邻居顶点的节点curr_node.children.append(child_node)  # 将该节点加入到当前节点的子节点列表中queue.append(child_node)  # 将该节点加入队列edge = graph.next(edge)roots.append(root)  # 将当前连通分量的根节点加入列表return roots

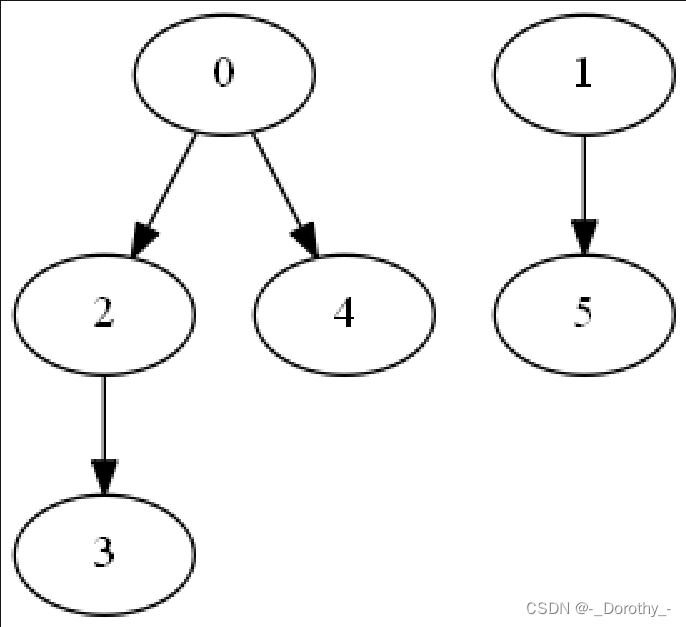
在这里插入图片描述
在这里插入图片描述

（3）图的遍历与连通性

图的遍历算法可以用来判断图的连通性。
对于无向图来说，若无向图是连通的，则从任一结点出发， 仅需一次遍历就能够访问图中的所有顶点；若无向图是非连通的，则从某一个顶点出发，一次遍历只能访问到该顶点所在连通分量的所有顶点，而对于图中其他连通分量的顶点，则无法通过这次遍历访问。对于有向图来说，若从初始点到图中的每个顶点都有路径，则能够访问到图中的所有顶点，否则不能访问到所有顶点。

5、最小生成树Minimunspanning—tree

  • 带权、连通、无向图的生成树中——权值之和最小的那棵
  • 最小生成树的性质：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/323869.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

记一次DNS故障导致用户无法充值的问题（下）

记一次DNS故障导致用户无法充值的问题（下）

上一篇说到DNS故障导致无法充值&#xff0c;后来我们通过拨测发现业务域名的解析目标地址被解析到了【127.0.0.1】IP。 1、联系阿里云厂商&#xff0c;通过沟通&#xff0c;阿里云反馈我们的域名被XX省通管单位封禁了&#xff0c;导致解析到了不正确的地址。 2、为了解决用户问…
阅读更多...
使用Simulink Test进行单元测试

使用Simulink Test进行单元测试

本文摘要&#xff1a;主要介绍如何利用Simulink Test工具箱&#xff0c;对模型进行单元测试。内容包括&#xff0c;如何创建Test Harness模型&#xff0c;如何自动生成excel格式的测试用例模板来创建测试用例&#xff0c;如何手动填写excel格式的测试用例模板来手动创建测试用例…
阅读更多...
面向新手在无人机竞速场景下的飞行辅助系统——浙大 FAST-Lab 高飞团队 ICRA 论文三项 Best Paper 入围

面向新手在无人机竞速场景下的飞行辅助系统——浙大 FAST-Lab 高飞团队 ICRA 论文三项 Best Paper 入围

恭喜浙江大学 FAST-Lab 钟宇航同学的论文 A Trajectory-based Flight Assistive System for Novice Pilots in Drone Racing Scenario 顺利发表 ICRA 2024&#xff0c;并同时入选三项 Finalist&#xff1a; the IEEE ICRA Best Conference Paper Awardthe IEEE ICRA Best Pape…
阅读更多...
git与gitlab

git与gitlab

目录 gitlab 下载与安装 重置管理员密码 邮箱配置 gitlab命令 git远程gitlab相关命令 gitlab的使用 设置中文 修改默认分支 创建群组并授权 新建项目/新建库 设置当前用户的sshkey Deploy Keys 计划管理 权限管理 gitlab的备份与恢复 git git 分布式版本控制 …
阅读更多...
mysql安装及基础设置

mysql安装及基础设置

关系型数据库 MySQL是一种关系型数据库管理系统&#xff0c;采用了关系模型来组织数据的数据库&#xff0c;关系数据库将数据保存在不同的表中&#xff0c;用户通过查询 sql 来检索数据库中的数据。 yum 方式安装 mysql # yum -y install mysql-server # systemctl start my…
阅读更多...
Linux -- 日志

Linux -- 日志

一 日志的重要性 在之前的编程经历中&#xff0c;如果我们的程序运行出现了问题&#xff0c;都是通过 标准输出 或 标准错误 将 错误信息 直接输出到屏幕上&#xff0c;以此来排除程序中的错误。 这在我们以往所写的程序中使用没啥问题&#xff0c;但如果出错的是一个不断在运行…
阅读更多...
快速上手prometheaus grafana 监控

快速上手prometheaus grafana 监控

介绍 prometheaus 一个定时输出指标数据的巡检组件&#xff1f; grafana 一个读取指标&#xff0c;可视化的提供了好看界面的组件&#xff1f; 教程 如何和springboot项目集成 【IT老齐153】超级实用&#xff01;十分钟掌握Prometheus与Grafana监控SpringBoot应用_哔哩哔哩_…
阅读更多...
计算机网络 备查

计算机网络 备查

OSI 七层模型 七层模型协议各层实现的功能 简要 详细 TCP/IP协议 组成 1.传输层协议 TCP 2.网络层协议 IP 协议数据单元&#xff08;PDU&#xff09;和 封装 数据收发过程 数据发送过程 1. 2.终端用户生成数据 3.数据被分段&#xff0c;并加上TCP头 4.网络层添加IP地址信息…
阅读更多...
luceda ipkiss教程 68：通过代码模板提高线路设计效率

luceda ipkiss教程 68：通过代码模板提高线路设计效率

在用ipkiss设计器件或者线路时&#xff0c;经常需要输入: from ipkiss3 import all as i3那么有什么办法可以快速输入这段代码呢&#xff1f;这里就可以利用Pycharm的 live template功能&#xff0c;只需要将文件&#xff1a;ipkiss.xml &#xff08;luceda ipkiss教程 68&…
阅读更多...
Docker快速搭建NAS服务——FileBrowser

Docker快速搭建NAS服务——FileBrowser

Docker快速搭建NAS服务——FileBrowser 文章目录 前言FileBrowser的搭建docker-compose文件编写运行及访问 总结 前言 本文主要讲解如何使用docker在本地快速搭建NAS服务&#xff0c;这里主要写如下两种&#xff1a; FileBrowser1&#xff1a;是一个开源的Web文件管理器&…
阅读更多...
QT功能 实现静态内容国际化实验

QT功能 实现静态内容国际化实验

文章目录 第一步&#xff1a;新建一个QT工程第二步&#xff1a;添加控件第三步&#xff1a;在pro文件中添加内容第四步&#xff1a;更新文件第五步&#xff1a;打开QT的Linguist第六步&#xff1a;添加翻译内容第七步&#xff1a;回到QT Creator中添加文件第八步&#xff1a;给…
阅读更多...
软考中级-软件设计师（九）数据库技术基础 考点最精简

软考中级-软件设计师（九）数据库技术基础 考点最精简

一、基本概念 1.1数据库与数据库系统 数据&#xff1a;是数据库中存储的基本对象&#xff0c;是描述事物的符号记录 数据库&#xff08;DataBase&#xff0c;DB&#xff09;&#xff1a;是长期存储在计算机内、有组织、可共享的大量数据集合 数据库系统&#xff08;DataBas…
阅读更多...
微服务总览

微服务总览

微服务保护 微服务总览 微服务总览 接入层&#xff1a;反向代理功能&#xff0c;可以将用户域名访问的地址以负载均衡的方式代理到网关地址&#xff0c;并且并发能力非常高&#xff0c;并且会采用主备nginx的方式防止nginx寄了&#xff0c;备份nginx监控主nginx状态&#xff0c…
阅读更多...
YOLOV5更换转置卷积，助力涨点！

YOLOV5更换转置卷积，助力涨点！

由于转置卷积是nn库自带的，所以我们直接找到models文件夹中的yolo.py文件中的 parse_model函数，再在如下图的地方添加转置卷积模块 # YOLOv5 🚀 by Ultralytics, AGPL-3.0 license """ YOLO-specific modules.Usage:$ python models/yolo.py --cfg yolov5s.…
阅读更多...
Spring AOP(2)

Spring AOP(2)

目录 Spring AOP详解 PointCut 切面优先级Order 切点表达式 execution表达式 切点表达式示例 annotation 自定义注解MyAspect 切面类 添加自定义注解 Spring AOP详解 PointCut 上面代码存在一个问题, 就是对于excution(* com.example.demo.controller.*.*(..))的大量重…
阅读更多...
FPGA -手写异步FIFO

FPGA -手写异步FIFO

一&#xff0c;FIFO原理 FIFO&#xff08;First In First Out&#xff09;是一种先进先出的数据缓存器&#xff0c;没有外部读写地址线&#xff0c;使用起来非常简单&#xff0c;只能顺序写入数据&#xff0c;顺序的读出数据&#xff0c;其数据地址由内部读写指针自动加1完成&a…
阅读更多...
案例研究｜硬之城借助DataEase以数据驱动供应链精细化管理

案例研究｜硬之城借助DataEase以数据驱动供应链精细化管理

深圳硬之城信息技术有限公司&#xff08;以下简称为“硬之城”&#xff09;成立于2015年&#xff0c;专注电子元件供应链领域&#xff0c;定位于电子产业供应链与智造平台。硬之城通过名为“Allchips”的集成式服务平台&#xff0c;为客户提供一站式的电子元件采购和供应链管理…
阅读更多...
ROS八股总结

ROS八股总结

1. 概述 ROS系统是为了提高机器人研发中的软件复用率&#xff0c;每个模块可以被单独设计与编译&#xff0c;运行时以松耦合的方式结合在一起。提供硬件抽象、底层驱动、消息传递、程序管理、应用原型等功能和机制。且集成了大量工具、库、协议 2.特点 点对点 节点单元分布式…
阅读更多...
动态规划——路径问题：LCR 166.珠宝的最高价值

动态规划——路径问题：LCR 166.珠宝的最高价值

文章目录 题目描述算法原理1.状态表示&#xff08;题目经验&#xff09;2.状态转移方程3.初始化4.填表顺序5.返回值 代码实现CJava 题目描述 题目链接&#xff1a;LCR 166.珠宝的最高价值 算法原理 1.状态表示&#xff08;题目经验&#xff09; 对于这种路径类的问题&…
阅读更多...
【全开源】Java外卖霸王餐免费吃外卖小程序+APP+公众号+H5多端霸王餐源码

【全开源】Java外卖霸王餐免费吃外卖小程序+APP+公众号+H5多端霸王餐源码

一、特色功能 霸王餐活动管理&#xff1a;允许商家发布和管理霸王餐活动&#xff0c;包括设置活动时间、具体优惠、活动规则等。用户参与与浏览&#xff1a;用户可以在小程序中浏览霸王餐活动列表&#xff0c;查看活动的详情信息&#xff0c;如商品或服务的免费赠送、活动规则…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023