【题目来源】
https://www.acwing.com/problem/content/2717/
【题目描述】
给定一个长度为 n 的字符串,只包含大小写英文字母和数字。
将字符串中的 n 个字符的位置编号按顺序设为 1∼n。
并将该字符串的 n 个非空后缀用其起始字符在字符串中的位置编号表示。
现在要对这 n 个非空后缀进行字典序排序,并给定两个数组 SA 和 Height。
排序完成后,用 SA[i] 来记录排名为 i 的非空后缀的编号,用 Height[i] 来记录排名为 i 的非空后缀与排名为 i−1 的非空后缀的最长公共前缀的长度(1≤i≤n)。
特别的,规定 Height[1]=0。
请你求出这两个数组。
【输入格式】
共一行,包含一个长度为 n 的仅包含大小写英文字母或数字的字符串。
【输出格式】
第一行包含 n 个整数,表示 SA 数组。
第二行包含 n 个整数,表示 Height 数组。
【数据范围】
1≤n≤10^6
【输入样例】
abababab
【输出样例】
7 5 3 1 8 6 4 2
0 2 4 6 0 1 3 5
【后缀树及后缀数组简介】
● 后缀(Suffix):字符串的后缀是指从字符串某个位置开始到末尾的所有子串。例如,字符串 s[]="abcdefg" 的后缀为 s[0]="abcdefg"、s[1]="bcdefg"、s[2]="cdefg"、s[3]="defg"、s[4]="efg"、s[5]="fg"、s[6]="g" 等。
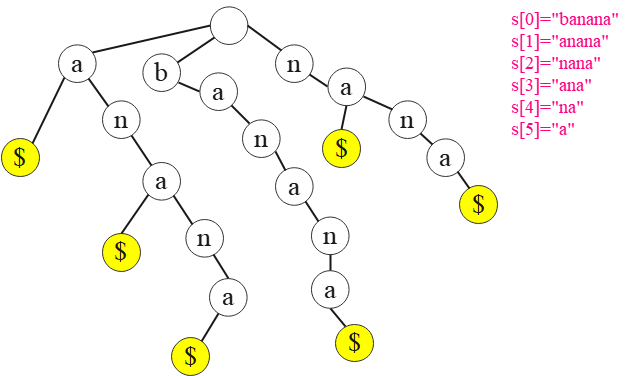
● 后缀树(Suffix Tree):将字符串的所有后缀子串用字典树的方法建立的树。换句话说,后缀树的本质是把一个长度为 n 的字符串拆成 n 个后缀子串,然后按字典序来构造。后缀树的根结点为空,后缀树中每个后缀子串的末尾用符号 $ 表示。
例如,字符串 s[]="banana" 的后缀为 s[0]="banana"、s[1]="anana"、s[2]="nana"、s[3]="ana"、s[4]="na"、s[5]="a",其对应的后缀树如图所示。
● 长度为 n 的字符串,其 n 个后缀子串的长度分别为 n,n-1,n-2,……,2,1,总长度为 n(n+1)/2。可见,后缀树的空间复杂度比较差,为 O(n^2)。故引入后缀数组 sa (Suffix Array)来代替后缀树。
● 后缀数组 sa(Suffix Array):后缀数组 sa 的值就是将字符串的所有后缀子串按字典序排序后对应的原始下标。
例如,字符串 s[]="banana" 的后缀为 s[0]="banana"、s[1]="anana"、s[2]="nana"、s[3]="ana"、s[4]="na"、s[5]="a",其对应的后缀数组 sa[]={5,3,1,0,4,2}。求解过程如下图所示。

● 后缀数组元素 sa[i],是原字符串中从第 i 个位置开始的后缀子串(下标从 0 开始)。例如,在上图所示后缀数组 sa 中,sa[1]=3,表示排名 1 的子串,是原字符串 banana 中从第 1 个位置开始的后缀子串,即 ana。
● 在后缀数组的代码实现中,有 3 个关键的数组:后缀数组 sa[]、名次数组 rk[]、高度数组 height[]。其中,sa[] 与 rk[] 是一一对应关系,互为逆运算。由 sa[] 数组推出 rk[] 数组在实战中常用。
由 rk[] 数组推出 sa[] 数组的代码如下所示:
for(int i=0; i<n; i++) sa[rk[i]]=i;由 sa[] 数组推出 rk[] 数组的代码如下所示:
for(int i=0; i<n; i++) rk[sa[i]]=i;例如,由上文已知,字符串 s[]="banana" 的后缀为 s[0]="banana"、s[1]="anana"、s[2]="nana"、s[3]="ana"、s[4]="na"、s[5]="a",其对应的后缀数组 sa[]={5,3,1,0,4,2}。
据 sa[] 数组推出 rk[] 数组的代码 rk[sa[i]]=i 可得:
rk[sa[0]]=rk[5]=0
rk[sa[1]]=rk[3]=1
rk[sa[2]]=rk[1]=2
rk[sa[3]]=rk[0]=3
rk[sa[4]]=rk[4]=4
rk[sa[5]]=rk[2]=5
由上显见,rk[i] 的值为原字符串的第 i 个后缀子串,在原字符串所有后缀子串按字典序排序后,其所处的位序。
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=1e6+5;//sa[i] 表示字典序排名为 i 的后缀处于原字符串所有后缀的位序
//rk[i] 表示原字符串第 i 个后缀的字典序排名
//height[i] 表示排名第 i 的后缀和排名第 i - 1 的后缀的最长公共前缀
//fi[i] 表示第 i 个后缀的第一关键字
//se[i] 表示第 i 个后缀的第二关键字
//c[i] 表示关键字为 i 的数的个数
int sa[maxn],rk[maxn];
int height[maxn];
int fi[maxn],se[maxn],c[maxn];char s[maxn];
int n,m;void get_sa() {for(int i=1; i<=n; i++) c[fi[i]=s[i]]++;for(int i=2; i<=m; i++) c[i]+=c[i-1]; //prefix sumfor(int i=n; i>=1; i--) sa[c[fi[i]]--]=i;for(int k=1; k<=n; k<<=1) {//Radix Sort based on 2nd keyint num=0;for(int i=n-k+1; i<=n; i++) se[++num]=i;for(int i=1; i<=n; i++)if(sa[i]>k) se[++num]=sa[i]-k;//Radix Sort based on 1st keyfor(int i=1; i<=m; i++) c[i]=0;for(int i=1; i<=n; i++) c[fi[i]]++;for(int i=2; i<=m; i++) c[i]+=c[i-1];for(int i=n; i>=1; i--) sa[c[fi[se[i]]]--]=se[i], se[i]=0;//Discretize all sorted suffixes according to the first 2K charactersswap(fi,se);fi[sa[1]]=1, num=1;for(int i=2; i<=n; i++) {if(se[sa[i]]==se[sa[i-1]] && se[sa[i]+k]==se[sa[i-1]+k]) fi[sa[i]]=num;else fi[sa[i]]=++num;}if(num==n) break;m=num;}
}void get_height() {for(int i=1; i<=n; i++) rk[sa[i]]=i;for(int i=1, k=0; i<=n; i++) {if(rk[i]==1) continue;if(k) k--;int j=sa[rk[i]-1];while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) k++;height[rk[i]]=k;}
}int main() {scanf("%s", s+1);n=strlen(s+1);m=122; //ASCII of 'z' is 122get_sa();get_height();for(int i=1; i<=n; i++) printf("%d ",sa[i]);printf("\n");for(int i=1; i<=n; i++) printf("%d ", height[i]);return 0;
}/*
in:
ababababout:
7 5 3 1 8 6 4 2
0 2 4 6 0 1 3 5
*/
【参考文献】
https://www.acwing.com/solution/content/163123/
https://www.acwing.com/solution/content/58924/