机器学习基础笔记

周志华老师的机器学习初步的笔记

绪论

知识分类

科学是什么，为什么

技术怎么做

工程多快好省

应用口诀，技巧，实际复杂环境，行行出状元

定义

经典定义 利用经验改善系统自身的性能

训练数据

模型学习算法分类

决策树，神经网络，支持向量机，boosting，贝叶斯网

测试数据

输出

重要理论

PAC (Probably Approximately Correct，概率近似正确),如公式所示

$\leq \epsilon) \geq 1 - \delta$ 即预测结果 $f (x)$ 落在允许误差 $\epsilon$ 内的概率在置信区间$ \delta$内

P问题，在多项式时间内能找到解，NP问题，在多项式时间内验证是不是解

基础

基本术语

数据集：训练，测试，测试集与训练集要不一样

示例：即西瓜的特征，样例：示例加上西瓜的好坏

样本：一个数据集或一个样例

属性、特征：即色泽，根蒂

分为离散和连续，离散又分为有序和无序

像颜色，可以直观上说无序，也可以根据光谱波长来说有序

属性空间，样本空间，输入空间：即样本点放在坐标系里面，以便于回归分析

特征向量：即一个示放在空间之中的结果

假设： $f (x)$ 我们的模型得到的结果本质是一个假设

真相： $y$ 真实结果

学习器：得到的学习结果，参数那种

分类，回归

二分类，多分类

正类，反类

无监督学习和监督学习的区别就是前者的数据集都没有标签，需要根据特征进行自行分类

监督学习里面有分类(class，类)和回归，分别对应无监督学习里面的聚类(cluster，簇)和密度估计

学习本质

我们假定所拿到的数据是满足某个未知分布的，所有数据都是独立同分布取出来的数据

而学习的数据只是这个分布里面的一部分，而我们训练的模型是否能够处理分布以外的数据

泛化，即 $\epsilon$ 能达到多小，只有降其降到足够小，我们才能够去设计算法

归纳偏好

使用奥卡姆剃刀原理，在多种合理理论的时候选择最简单的理论

所以机器学习在处理不同类型的问题有不同的模型

NFL定理：no free lunch，一个模型在满足了部分数据集就必然不能满足另外一部分，不同模型各有优劣，一个问题的不同部分可能使用多个模型

具体问题具体分析，要明确输入输出才是问题，即x，y。分类不算一个问题

误差

经验误差，在训练集上的误差，采用参数优化，一般为梯度下降

泛化误差，在未来样本的误差，采用正则化，防止过拟合

正则化和正则表达式没有任何关系，可能会因为我们学习的过拟合认为二者有联系

而我们机器学习的过程就是不断降低经验误差的过程

但是泛化误差却是一个u型曲线，先逐渐下降，再逐渐上升，即欠拟合和过拟合

所以在一直下降的经验误差中，找到最小的泛化误差是一个难点

但这个问题也没有确切的解决方案，所以不同的模型其实是在使用不同的方案缓解过拟合

了解缓解过拟合的方法是学习新模型的首要目的

正则化

如在多项式拟合中针对参数正则化，因为越高阶的参数在过拟合时，数值上会更大

为了防止高阶参数的影响过大，而自己也不需要去指定多少阶，所以我们的原始损失函数后面加上正则化项来表示总损失函数

而正则化我们一般使用L1和L2正则化，即一阶和二阶正则化

使用L1正则化 $L_{\mathrm{total}}=L+\lambda\sum_i|w_i|$

使用L2正则化 $L_{\mathrm{total}}=L+\frac\lambda2\sum_iw_i^2$ 这里的1/2是为了求导方便

L为原始损失函数，一般为均方误差 $\mathrm{MSE}=\frac1m\sum_{i=1}^m\sum_{j=1}^n\left(\hat{y}_{ij}-y_{ij}\right)^2$

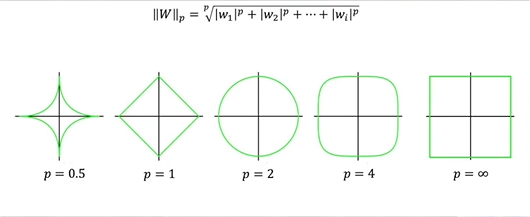
范数

这里的L1和L2在数学里叫做范数，用来表示向量的大小,下面是 $L_p$ 范数的基本形式
$\|\mathbf{v} \|_p = \left( \sum_{i=1}^{n} |v_i|^p \right)^{1/p}$

范数.png

评估模型

评估方法

关键在于如何得到测试集？

留出法：将数据集分割为训练集和测试集

要分层采样，多次训练切分进行平均，一般进行4:1分。最后将所有数据集进行训练得到模型

极端的情况，留一法：每次留一个来进行测试，虽然得到的结果与全部数据用来训练相近，但这样会导致未来误差不准确

k-折交叉验证法：解决留出法中未能将全部数据集用于训练和验证，而数据集所有都很重要的时候

将数据集划分为k份，依次取一份来当测试集。而这个划分也可能对结果产生影响，所以也进行k次划分，即为10*10的验证

自助法：(bootstrap sampling)将样本分为n包，每次有放回的取n包出来，将没有取出过的作为测试集，也叫包外估计

m个样本取m次，没有取到的概率为

$\lim_{m\to\infty}\left(1-\frac1m\right)^m=\frac1e\approx0.368$

因为这样改变了训练数据的分布，所以在数据不那么重要的时候使用

调参数

算法参数，如用n次曲线去回归的这个n，一般由人工设定，称为超参数

模型参数，由训练数据集训练的得到的参数，即权重(weight)和偏置(bias)

验证集，将训练集分割一部分出来，用于评估选择的模型是否合适，如验证超参数，如果合适再合并一起训练

性能度量

即损失函数最小

如回归任务常用的均方误差， $E(f;D)=\frac1m\sum_{i=1}^m\left(f\left(\boldsymbol{x}_i\right)-y_i\right)^2$

而像logistic回归，使用交叉熵损失函数

像分类问题，分类结果混淆矩阵 p为positive，n为negative

$\begin{array}{c|c|c}\hline&\text{预测结果}\\\hline\text{真实情况}&\text{正例}&\text{反例}\\\hline\text{正例}&TP\text{ (真正例)}&FN\text{ (假反例)}\\\hline\text{反例}&FP\text{ (假正例)}&TN\text{ (真反例)}\\\hline\end{array}$

查准率 $P=\frac{TP}{TP+FP}$ 查全率 $R=\frac{TP}{TP+FN}$

可以用这两种来进行评估不同模型的好坏

我们综合二者得到 $\frac{1}{F1}=\frac{1}{2}\cdot\left(\frac{1}{P}+\frac{1}{R}\right)$ 使用调和平均，让二者都能保持较高的值，也可以对偏好的加上权重，如 $\frac{1}{F_\beta}=\frac{1}{1+\beta^2}\cdot\left(\frac{1}{P}+\frac{\beta^2}{R}\right)$ 通过设置 $\beta$ 的值来设定谁更重要

比较检验

使用概率论的假设检验

对于两个不同的算法得到错误率，然后相减得到x，我们多次训练，得到X矩阵

经典模型

线性模型

基础

分类，一条线划分两边

回归，一条线穿所有点

函数如下 $f(x)=w_1x_1+w_2x_2+\ldots+w_dx_d+b$ 向量形式 $f(x)=w^\mathrm{T}x+b$

因为线性模型是对数值进行处理，所以我们需要将属性转换为样本

对无序的属性，如颜色，使用二进制编码转换，每一位表示一种颜色，编码为0001,0010,0100,1000这种

而对于多元求解，而矩阵未满秩，会求出多个解，我们采用归纳偏好，取某个w为最小或最大，这个过程也称为正则化，来防止我们模型过拟合

对数线性回归

即 $lnf(x)=w^\mathrm{T}x+b$ ，这里的ln称为联系函数g，必须单调可微

这里，我们需要将结果转化为[0,1]的结果，来进行分类

我们这里找到对数几率函数 $y=\frac{1}{1+e^{-z}}$ z为f(x)

将其代入后得到 $\ln\frac y{1-y}=w^\mathrm{T}x+b$ 而 $\frac y{1-y}$ 就是odds，几率，正反概率之比，也就是对数几率函数的名称来源

使用残差和得到的函数无法求解最小值，所以我们使用极大似然估计得到损失函数
$\ell\left(\boldsymbol{\beta}\right)=\sum_{i=1}^m\left(-y_i\boldsymbol{\beta}^\mathrm{T}\hat{\boldsymbol{x}}_i+\ln\left(1+e^{\beta^\mathrm{T}\hat{\boldsymbol{x}}_i}\right)\right)$
该函数也称为交叉熵损失函数，使用梯度下降来求解极值，与求导相比，计算机更擅长，也更加通用

线性判别分析

Linear Discriminant Analysis 简称LDA

如图，降维到一条直线上，使得不同类别分开，同一样本紧凑

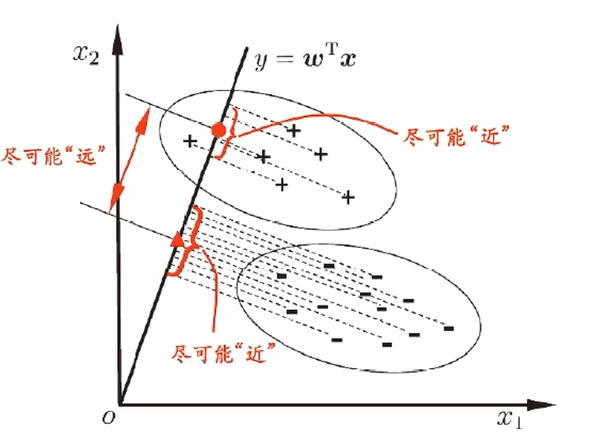
定量计算就是最大化广义瑞利商， $S_b$ 为组间散度矩阵 $S_w $ 为组内散度矩阵，用这两个投影来表示距离，J越大越好
$J=\frac{w^\mathrm{T}\mathrm{S}_bw}{w^\mathrm{T}\mathrm{S}_ww}$
最后得到 $
\boldsymbol{w}=\mathbf{S}_w^{-1}\left(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\right)
$
其中由奇异值分解得到 $\mathbf{S}_{w}^{-1}=\mathbf{V}\Sigma^{-1}\mathbf{U}^{\mathrm{T}}$

多分类

采用投票机制，怎么比较又分为OvO和OvR

OvO，One-vs-One

讲一个任务拆解成若干个二分类任务，如四分类，就分为 $C_4^2=6$ 组，将被测对象输入着六个二分类模型，输出结果最多的就是我们的最终结果

如果打平，可以加入置信度的选择，如对数几率，直接比较输出的值的和，而不是用0,1比较

OvR，One-vs-Rest

将自己和其余的进行训练，分为正负类，哪个模型输出为正类就选哪个

比较

前者训练时间短，容易做并行化；后者训练模型更少，存储开销和测试时间更大。

二者预测性能差不多，选择在时间还是空间上进行取舍

类别不平衡

当小类占比很小，但又很重要的时候，我们一般采取下面的方法。

平衡采样，过采样小类或者欠采样大类。

过采样采用在小类样本之间插值的方法，而不是直接复制
欠采样则在大类中每次采取与小类数量相同的样本，多彩采样训练后投票

阈值移动，如在对数几率回归中，我们原本取0.5作为分界，即1/1，而我们可以根据二者的比例调整为m/n。支持向量机

决策树

递归停止条件

如图所示，我们通过递归调用，直到走到叶节点的时候，判断是否为好瓜

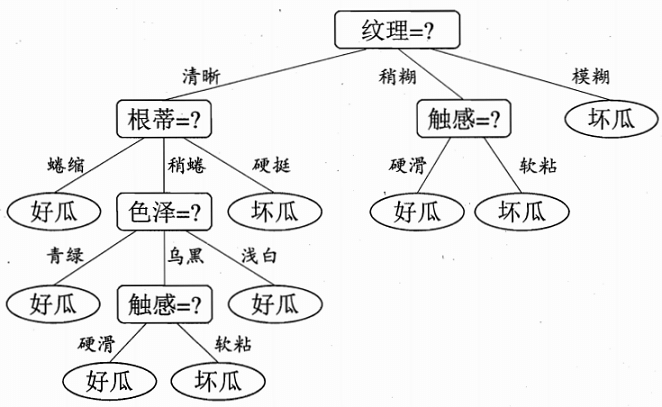
因为树是递归调用，所以我们需要设置停止条件

如果一条线已经用完所有属性了，还是没有分离开。如分类数大于属性数的时候
如果训练数据集中不包含某一组合数据，如根蒂稍蜷中没有色泽浅白的，那么这个叶节点就由色泽节点中数量多的一类决定
如果已经完全分类了，多的属性也不需要继续看了，停止，如纹理模糊的一类

信息增益

由此可见，如何确定节点的顺序对分类很重要，越容易区分类型的节点越靠前

我们引入信息熵的概念来表示第k类样本的纯度，便于计算

其中p表示第k类的占比(概率)，计算p=0或1时，Ent为0，即当分类完成时，信息熵为0
$\operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|}p_k\log_2p_k$
所以就是一直降第每个节点的信息熵，所以选择信息熵最小的作为第一个节点，依次类推

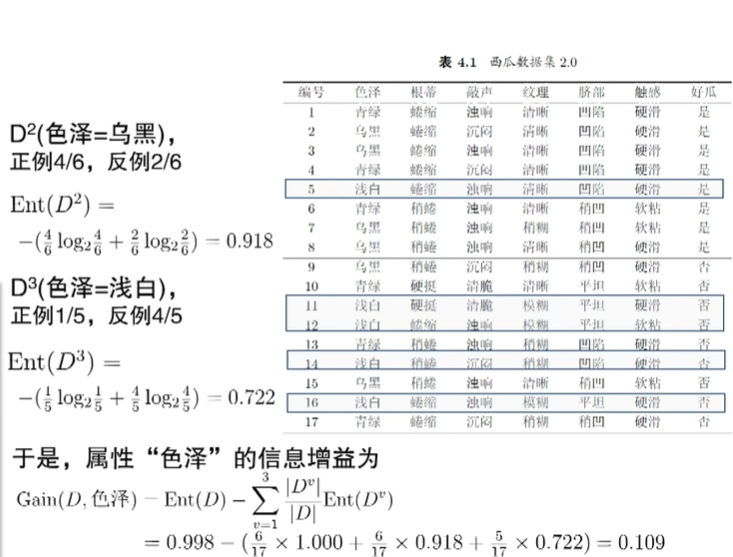
如图，计算了色泽的信息增益，将其他属性一起计算，选出第一层为纹理

然后再这样一直操作，得到决策树如一开始所示

增益率

考虑到极端情况，如果按身份证号将人分类，那么依次就能将所有人区分，信息增益最大。

但这样显然没有意义，所以我们改进，将信息增益除以a的可能性的信息熵，即a可能的数目应该越小越好。但分子分母的取向是鱼和熊掌不可兼得的，所以需要自己取舍

使用启发式来取舍，将信息增益高于平均的找出来再取增益率最高的
$\mathrm{Gain_ratio}(D,a)=\frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)}\\\text{其中}\mathrm{IV}(a)=-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}\log_{2}\frac{|D^{v}|}{|D|}$

CART决策树

前面是使用信息熵来表示纯净度，这里使用基尼指数来表示纯度

基尼指数用于表示国家或地区收入不平等程度的统计指标，取值为[0,1]。

如果基尼指数为0，则代表收入完全平等，同理，也表示分类越纯净。
$\begin{aligned}\operatorname{Gini}(D)&=\sum_{k=1}^{|\mathcal{Y}|}\sum_{k^{\prime}\neq k}p_{k}p_{k^{\prime}}\\&=1-\sum_{k=1}^{|\mathcal{Y}|}p_{k}^{2}.\end{aligned}$
这里的意思是取到两次不同的概率。如果纯净，那么结果应该为0

性能优化

使用不同来描述纯净度，如信息熵和基尼指数影响只有2%，而减枝可以缓解过拟合，将泛化性能提升约25%

防止决策树上学到的不是一般规律，而是少数几个个体的特征

预剪枝：提前终止某些分支生长，如设置纯净度略大于0，而不是绝对为0，增加泛化能力

后剪枝：生成完全树后再取删除

缺失值

如果一个样本缺失了某一属性，如果直接弃用，可能会破坏原有分布。当属性过多时，很难避免缺失，可能会对数据造成极大的浪费

我们采用样本赋权，权重划分的方式。

样本赋权：即利用未缺失样本来算纯净度，然后将纯净度乘以未缺失的占比，来得到节点顺序

权重划分：将缺失的项目按照已知样本各类的权重来分配到几个类别中，从而利用缺失值样本

神经网络

概念

定义：神经网络是由具有适应性的简单单元组成的广泛并行互联的网络

一个神经元包含一个带权公式，连接多个输入，当计算达到阈值时输出结果

如图所示神经元模型，每个神经元相当于线性模型加上激活函数，使用sigmoid函数(S形，一般用logistic函数)来表示激活

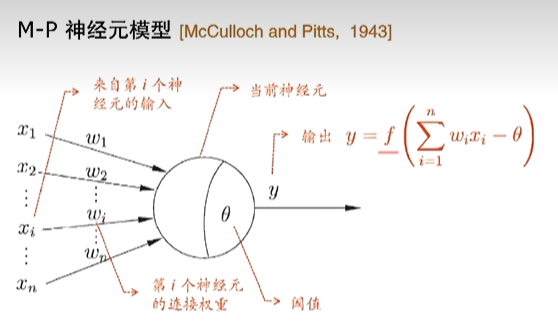
神经网络由多个神经元联系而成,如下，除去输入和输出层，其他的层叫做隐层。

输出层和隐层神经元称为功能单元

Neural networks.png

只要有一个包含足够多神经元的隐层，就可以以任意精度逼近任意复杂的连续函数，具有万有逼近性

傅里叶变换，泰勒展开同样可以，因为神经网络数学基础薄弱，训练过程盲盒，所以需要理论支撑。并不是因为这个而比其他模型强多少

所以问题就在于如何设置神经元数，采用试错法，根据问题复杂性，自己调节

BP算法

同样使用梯度下降，对于调整学习率 $\eta$ 可以先快，后慢。如一直减半

支持向量机

基础

主要思想：找到一个能够将不同类别的样本分隔开的超平面，并且使得该超平面与最近的样本点(也称支持向量)之间的间隔最大化。

直接调包解

高维空间映射

如果不能用平面分开，则将样本映射到更高维特征空间，然后就有一个高维超平面可以实现我们的效果，如下图所示

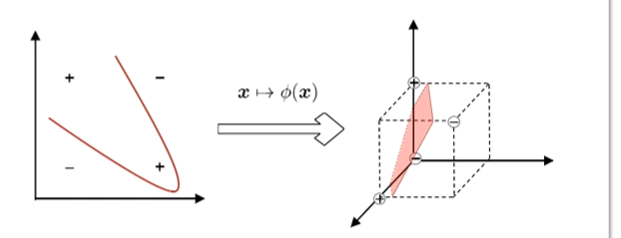
高维特征空间映射.png

而映射后的高维向量在最终结果中只以内积形式出现，所以我们可以避免求解高维向量，使用核函数来代替求高维向量的内积。

一个对称函数对应的核矩阵半正定，就可以作为核函数。说人话就是这个函数可以作为高维空间的距离函数来使用。

任何一个核函数，都定义了一个RKHS(再生核希尔伯特空间，有点中二的感觉),说人话就是那个高维空间

因为核函数的选择上，存在不确定性，无法找到最优

应用回归

思路，落在$2\epsilon $范围内的不计算损失，其他的就按照距离之类的计算损失

主要是根据问题可以自己设计损失函数

贝叶斯决策论

通过计算把一个样本分到某类的错误概率，错误概率最小的那个类就是我们所选的分类

贝叶斯公式

分到某一类的条件风险 $R(c_i\mid\boldsymbol x)=\sum_{j=1}^N\lambda_{ij}P(c_j\mid\boldsymbol x)$

贝叶斯判定准则，即选择风险最小的一个 $h^*(\boldsymbol{x})=\underset{c\in\mathcal{Y}}{\operatorname*{\arg\min}}R(c\mid\boldsymbol{x})$

其中

c表示class，类别
$h^*$ 称为贝叶斯最优分类器
$\lambda_{ij}$ 表示将j类分到i类产生的损失，由我们权衡利弊得到
$P(c_j\mid\boldsymbol x)$ 表示x属于第j类的概率，通常难以获得，贝叶斯的角度下，机器学习就是算这个

根据获得这个后验概率的不同方式，可以分为两类

判别式模型：决策树，BP神经网络，SVM

直接对 $P(c\mid\boldsymbol x)$ 建模
生成式模型：贝叶斯分类器

先对联合概率分布 $P (x, c)$ 建模，再由此获得 $P (c ∣ x)$ ,即还原x的分布
$P(c\mid x)=\frac{P(x,c)}{P(x)}$

哲学

贝叶斯学习一定使用的分布估计，与贝叶斯分类器不一样，与先前求出最好的参数不同，贝叶斯学习认为参数也是满足一个分布，基于此分布观察到参数，即找到决定参数的分布

根据支持向量机的发明人的看法，我们解决的只是一个简单的问题，但使用贝叶斯就会把这个问题更复杂，虽然更加的全面，但也更加的低效，事物的两面，只需要找参数的点估计

贝叶斯学习认为，不搞清楚本质分布，就无法准确描述所需解决的问题

频率主义和贝叶斯主义都会用到贝叶斯公式，角度不一样，不能以此来区分

朴素贝叶斯分类

对每个属性求其在每个类别的概率，如颜色青绿为好瓜的概率为0.6，其他属性类似

拿到一个测试样本，如下求出两类的概率，再比较大小进行分类。
$\begin{aligned} &\mathsf{P}(\text{青绿}|\text{好瓜})\mathsf{P}(\text{稍蜷}|\text{好瓜})\mathsf{P}(\text{浊响}|\text{好瓜}) \\ &\mathsf{P}(\text{清晰}1\text{好瓜})\mathsf{P}(\text{好瓜=yes})=3/8\times3/8 \\ &\times6/8\times7/8\times8/17 \\ &\mathsf{P}(\text{青绿}|\text{坏瓜})\mathsf{P}(\text{稍蜷}|\text{坏瓜})\mathsf{P}(\text{浊响}|\text{坏瓜}) \\ &\mathsf{P}(\text{清晰}|\text{坏瓜})\mathsf{P}(\text{好瓜=no})=3/9\times4/9\times \\ &4/9\times2/9\times9/17 \end{aligned}$

集成学习

简介

即集成使用多个模型来解决问题

如果多个模型都是相同的，就成为同质集成，如神经网络集成，因为只需要一个模型，会比较简单

如果多个模型不同，就成为异质集成，由于不同模型产生的结果不能直接比较，就像同一门课，对同一个人的问卷，不同老师可能打的分差别很大一样，在处理结果时，要进行配准，这一步很困难

集成学习有可能出现下面三种情况

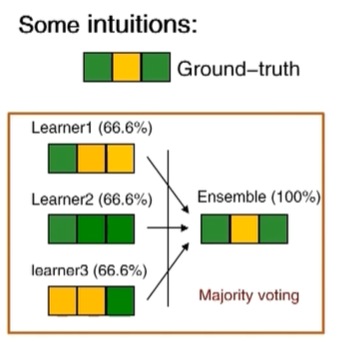
集成学习1.png
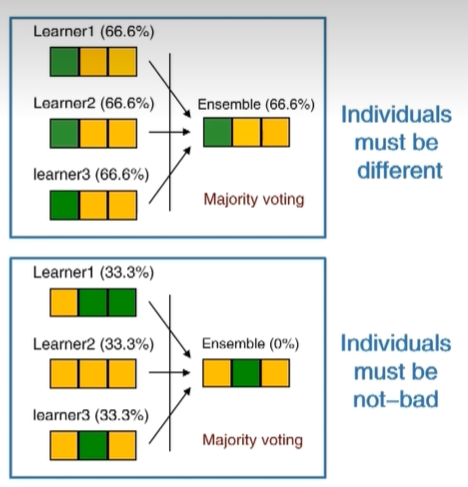
集成学习2.png

由此可见，集成不能乱集成，我们可以使用误差-分歧分解来衡量

即总误差 = 个体平均误差 - 个体平均差异

即我们要求平均误差小，个体差异大，但个体差异无法进行准确的衡量

多样性

使用不同的统计量，如相关系数，不合度量，q统计量，kapa统计量

目前有很多的度量方式，仍然是个难以解决的问题

聚类

无监督学习中应用最广的，其目的是将没有标签的数据分类成不同的簇，使簇内相似度高，簇间相似度低

这里面的差异用距离来衡量

距离

因为我们拿到的属性可能是离散值，所以我们需要将其转换为有序，无序或者混合属性

对有序属性使用Minkowski距离如下，用来表示距离的通式
$\operatorname{dist}_{\operatorname{mk}}(\boldsymbol{x}_i,\boldsymbol{x}_j)=\left(\sum_{u=1}^n|x_{iu}-x_{ju}|^p\right)^{\frac{1}{p}}$

p=2：欧式距离，即我们几何上的距离
p=1：曼哈顿距离，只考虑水平和垂直方向的距离，在解决网格结构时很好用

对无序属性可使用VDM(value difference metric) ，用不同属性出现的机会来评估他们是否相似
$VDM_p(a,b)=\sum_{i=1}^k\left|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\right|^p$

对混合属性，将二者组合
$\mathrm{MinkovDM}_p(\boldsymbol{x}_i,\boldsymbol{x}_j)=\left(\sum_{u=1}^{n_c}|x_{iu}-x_{ju}|^p+\sum_{u=n_c+1}^n\mathrm{VDM}_p(x_{iu},x_{ju})\right)^{\frac{1}{p}}$
后面两个都看不懂了，先记着