DAY44

闫氏DP

2 01背包问题

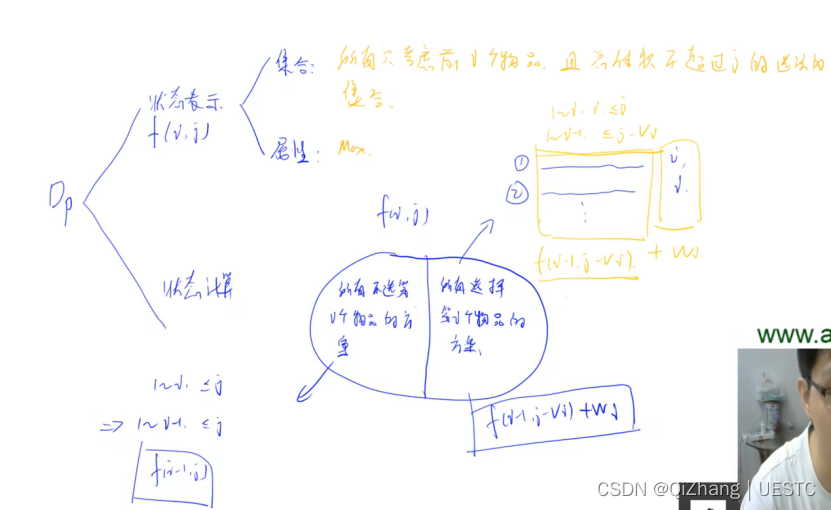
用滚动数组来优化空间，从后向前（大到小）遍历j

1. #include<iostream>
2. using namespace std;
3. const int N=1010;
4. int n,m;
5. int v[N],w[N];
6. int f[N][N];//所有只考虑前i个物品，**且总体积不超过j**的选法的集合。
7. int main(){
8.     cin>>n>>m;
9.     //背包当前体积j 是第二维度
10.     for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
11.     for(int i=1;i<=n;i++){
12.         //从0开始检查：前i个物体，使得背包体积为0，合法吗：合法，因为可以都不选
13.         for(int j=0;j<=m;j++){
14.             f[i][j]=f[i-1][j]; //left;
15.             //右半边不一定存在，当前体积小于v[i]，但是i又在背包。矛盾，不合法
16.             //这里因为只计算变的情况下对应的当前背包体积，所以是[j-v[i]]
17.             if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
18.         }
19.     }
20.     cout<<f[n][m]<<endl;
21.     return 0;
22. }

空间优化：

1. #include<iostream>
2. using namespace std;
3. const int N=1010;
4. int n,m;
5. int v[N],w[N];
6. int f[N];//所有只考虑前i个物品，**且总体积不超过j**的选法的集合。
7. int main(){
8.     cin>>n>>m;
9.     //背包当前体积j 是第二维度
10.     for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
11.     for(int i=1;i<=n;i++)
12.         //从0开始检查：前i个物体，使得背包体积为0，合法吗：合法，因为可以都不选
13.         for(int j=m;j>=v[i];j--)
14.          f[j]=max(f[j],f[j-v[i]]+w[i]);
15.     cout<<f[m]<<endl;
16.     return 0;
17. }

优化思想：代码等价即可。

完全背包问题

记：把01背包问题改成for(int j=v[i];j<=m;j++)即可

笔记见纸质版。

J=0 或j=1起步都可以

1. #include<iostream>
2. using namespace std;
3. const int N=1010;
4. int n,m;
5. int v[N],w[N];
6. int f[N][N];
7. int main(){
8.     cin>>n>>m;
9.     for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
10.     for(int i=1;i<=n;i++){
11.         for(int j=1;j<=m;j++){
12.             f[i][j]=f[i-1][j];
13.             if(j>=v[i]) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
14.         }
15.     }
16.     cout<<f[n][m]<<endl;
17.     return 0;
18. }

01背包问题 二维

1. 暴力法：回溯

回溯算法--01背包问题_回溯法01背包问题-CSDN博客

学过了吗：学好了，但是和代码随想录的回溯模板不一样，不太适应。比较陌生，看来需要二刷回溯。

1. 二维数组法：

1. #include<iostream>
2. using namespace std;
3. const int N=5010;
4. int v[N],w[N];
5. int dp[N][N];
6. int n,m;
7. int main(){
8.     cin>>n>>m;
9.     for(int i=1;i<=n;i++) cin>>v[i];
10.     for(int i=1;i<=n;i++) cin>>w[i];
11.     
12.     for(int i=1;i<=n;i++){
13.         for(int j=0;j<=m;j++){
14.             dp[i][j]=dp[i-1][j];
15.             if(j>=v[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
16.         }
17.     }
18.     cout<<dp[n][m];
19.     return 0;
20. }

1. 滚动数组优化

1. #include<iostream>
2. using namespace std;
3. const int N=5010;
4. int v[N],w[N];
5. int dp[N];
6. int n,m;
7. int main(){
8.     cin>>n>>m;
9.     for(int i=1;i<=n;i++) cin>>v[i];
10.     for(int i=1;i<=n;i++) cin>>w[i];
11.     
12.     for(int i=1;i<=n;i++){
13.         for(int j=m;j>=v[i];j--){
14.             dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
15.         }
16.     }
17.     cout<<dp[m];
18.     return 0;
19. }

01背包问题 一维

也就是3.滚动数组优化

416分割等和子集

1. 贪心法，做不了，看例子：

1. 动态规划：据说是01背包的应用，但是我想不出来怎么应用

这样想（也是我没想出来的点）：两个子集的各自sum相等，那么它们的SUM应当等于原集合sum/2

// 每一个元素一定是不可重复放入，所以从大到小遍历

01背包问题：动态规划的思路一个一个物品去尝试，一点点扩大考虑能够容纳的容积大小，整个过程像是在填一张二维表格。

这题：设置状态：dp[i][j]表示考虑下标[0,i]这个区间里的所有整数，在它们当中是否能够选出一些数，使得这些数之和恰好为整数j。

优质题解，还分享了很多资料。

注意闫氏DP法的运用：在声明数组含义时候，需要明白每个下标的含义，然后再去denote DP数组的含义——满足**条件（每个下标）的**，再表示它的值。

学了很久，终于开始写代码了，见证自己的毅力哈哈：

1. class Solution {
2. public:
3.     //代码随想录解法：能用一维就用一维，语句复杂反而不容易通过。
4.     bool canPartition(vector<int>& nums) {
5.         int sum=0;
6.         for(auto n:nums) sum+=n;
7.         if(sum%2==1) return false;
8.         sum/=2;
9.         vector<int> dp(20010,0);
10.         for(int i=0;i<nums.size();i++){
11.             for(int j=sum;j>=nums[i];j--){
12.               dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);
13.             }
14.         }
15.         return dp[sum]==sum;
16.     }
17. };

1. class Solution {
2. public:
3. //二维力扣题解：
4.     bool canPartition(vector<int>& nums) {
5.         int sum=0;
6.         for(int n:nums) sum+=n;
7.         if(sum%2==1) return false;
8.         sum/=2;
9.         int len=nums.size();
10.         vector<vector<bool>> dp(len,vector<bool>(sum+1,false));
11.         for(int i=0;i<len;i++) {
12.             dp[i][0]=true;
13.         }
14.         if(sum>=nums[0]) dp[0][nums[0]]=true;
15.         //这里下标有细节,配合上一句一起用,那么i从1开始
16.         for(int i=1;i<len;i++){
17.             for(int j=0;j<=sum;j++)
18.             {
19.                 //别写错
20.                 dp[i][j]=dp[i-1][j];
21.                 if(j>=nums[i]) dp[i][j]=dp[i][j]||dp[i-1][j-nums[i]];
22.             }
23.         }
24.         return dp[nums.size()-1][sum];
25.     }
26. };

1. class Solution {
2. public:
3. //力扣官方+一维滚动数组
4.     bool canPartition(vector<int>& nums) {
5.         int sum=0,max=INT_MIN;
6.         for(auto n:nums) {
7.             sum+=n;
8.             if(n>max) max=n;
9.         }
10.         if(sum%2==1) return false;
11.         sum/=2;
12.         if(max>sum) return false;
13.         vector<bool> dp(sum+1,false);
14.         dp[0]=true;
15.         //照抄上一行，所以是i=1开始
16.         for(int i=1;i<nums.size();i++){
17.             //从后向前遍历
18.             for(int j=sum;j>=nums[i];j--)
19.             dp[j]=dp[j]||dp[j-nums[i]];
20.         }
21.         return dp[sum];
22.     }
23. };

1. class Solution {
2. public:
3.     // 精选题解：
4.     bool canPartition(vector<int>& nums) {
5.         int sum = 0;
6.         for (auto n : nums)
7.             sum += n;
8.         if (sum % 2 == 1)
9.             return false;
10.         sum /= 2;
11.         vector<vector<bool>> dp(nums.size(), vector<bool>(sum + 1, false));
12.         if (sum >= nums[0])
13.             dp[0][nums[0]] = true;
14.         for (int i = 1; i < nums.size(); i++) {
15.             for (int j = 0; j <= sum; j++) {
16.                 dp[i][j] = dp[i-1][j];
17.                 if (nums[i] == j) {
18.                     dp[i][j] = true;
19.                     continue;
20.                 }
21.                 if (j > nums[i])
22.                     dp[i][j] = dp[i][j] || dp[i-1][j - nums[i]];
23.             }
24.         }
25.         return dp[nums.size() - 1][sum];
26.     }
27. };

1. class Solution {
2. public:
3.     // 精选题解：
4.     bool canPartition(vector<int>& nums) {
5.         int sum = 0;
6.         for (auto n : nums)
7.             sum += n;
8.         if (sum % 2 == 1)
9.             return false;
10.         sum /= 2;
11.         vector<vector<bool>> dp(nums.size(), vector<bool>(sum + 1, false));
12.         if (sum >= nums[0])
13.             dp[0][nums[0]] = true;
14.         for (int i = 1; i < nums.size(); i++) {
15.             for (int j = 0; j <= sum; j++) {
16.                 dp[i][j] = dp[i-1][j];
17.                 if (nums[i] == j) {
18.                     dp[i][j] = true;
19.                     continue;
20.                 }
21.                 if (j > nums[i])
22.                     dp[i][j] = dp[i][j] || dp[i-1][j - nums[i]];
23.                 if(dp[i][sum]) return true;
24.             }
25.         }
26.         return dp[nums.size() - 1][sum];
27.     }
28. };

1. class Solution {
2. public:
3.     // 精选题解：
4.     bool canPartition(vector<int>& nums) {
5.         int sum = 0;
6.         for (auto n : nums)
7.             sum += n;
8.         if (sum % 2 == 1)
9.             return false;
10.         sum /= 2;
11.         vector<bool> dp(sum+1, false);
12.         dp[0] = true;
13.         //下一句不能少：他作为第一行
14.         if(sum>=nums[0]) dp[nums[0]]=true;
15.         for (int i = 1; i < nums.size(); i++) {
16.             for (int j = sum; j >= nums[i]; j--) {
17.                  dp[j] = dp[j] || dp[j - nums[i]];
18.             }
19.         }
20.         return dp[sum];
21.     }
22. };