目录
一,3162. 优质数对的总数 I
二,3163. 压缩字符串 III
三,3164. 优质数对的总数 II
四, 3165. 不包含相邻元素的子序列的最大和
一,3162. 优质数对的总数 I

假设 x 是 nums1 数组中的值,y 是 nums2 数组中值,我们要求的就是有几个 (x,y) 满足
x % (y * k) == 0,可以直接暴力
代码如下:
class Solution {public int numberOfPairs(int[] nums1, int[] nums2, int k) {int ans = 0;for(int x : nums1){for(int y : nums2){if(x%(y*k)==0) ans++;}}return ans;}
}二,3163. 压缩字符串 III

本题是一道模拟题,遍历word字符串,将相邻且字符相同的子字符串,写成数字+字符的形式,比如 "aaabbc",写成 "3a2b1c",注意,数字最大是9,也就是说如果遇到比如12个连续的'a',我们要写成 "9a3a"。
代码如下:
class Solution {public String compressedString(String word) {int cnt = 1;char[] ch = word.toCharArray();StringBuilder res = new StringBuilder();for(int i=1; i<ch.length; i++){if(ch[i] == ch[i-1] && cnt < 9){cnt++;}else{res.append(cnt);res.append(ch[i-1]);cnt = 1;}}if(cnt > 0){res.append(cnt);res.append(ch[ch.length-1]);} return res.toString();}
}三,3164. 优质数对的总数 II

1. 预处理被除数:
- 要求满足 x % (y * k) == 0 的数对(x,y),可以先枚举nums1数组,使用哈希表统计出 x / k 的所有因子及其对应的数量,再枚举 nums2 数组,看 y 是否是x/k的因子(即是否在哈希表中),如果存在,加上对应的值。最终得出答案
2.预处理除数
- 除了上述做法,我们还可以先枚举nums1数组,使用哈希表统计出 x / k 及其对应的数量,枚举nums2数组,枚举 y 的倍数及其数量,看是否在哈希表中,如果存在,加上对应的值。最终得出答案
代码如下:
class Solution {//预处理被除数xpublic long numberOfPairs(int[] nums1, int[] nums2, int k) {Map<Integer, Integer> map = new HashMap<>();for(int x : nums1){//统计 <x/k 的因子, 对应的数量>if(x%k == 0){for(int i=1; i<=Math.sqrt(x/k); i++){if(x/k%i == 0){map.merge(i, 1, Integer::sum);if(i < x/k/i)map.merge(x/k/i, 1, Integer::sum);}}}}long ans = 0;for(int y : nums2){ans += map.getOrDefault(y, 0);}return ans;}
}class Solution {//预处理除数ypublic long numberOfPairs(int[] nums1, int[] nums2, int k) {//O(n+m+(mx/k)logm)Map<Integer, Integer> map1 = new HashMap<>();long mx = 0;for(int x : nums1){//统计 <x/k,x/k的数量>if(x%k == 0){map1.merge(x/k, 1, Integer::sum);mx = Math.max(mx, x/k);}}Map<Integer, Integer> map2 = new HashMap<>();for(int y : nums2){map2.merge(y, 1, Integer::sum);}long ans = 0;for(int y : map2.keySet()){ int s = 0;for(int j=y; j<=mx; j+=y){//枚举 y 的倍数s += map1.getOrDefault(j, 0);}ans += (long) s * map2.get(y);}return ans;}
}四, 3165. 不包含相邻元素的子序列的最大和

本题一看就是一道标准的打家劫舍问题,直接上代码:
class Solution {public int maximumSumSubsequence(int[] nums, int[][] queries) {int MOD = (int)1e9 + 7;int n = nums.length;int[] f = new int[n];int ans = 0;for(int[] q : queries){nums[q[0]] = q[1];f[0] = Math.max(0, nums[0]);for(int i=1; i<n; i++){f[i] = Math.max(f[i-1], (i>1?f[i-2]:0)+nums[i]);}System.out.println(f[n-1]);ans = (ans+f[n-1])%MOD;}return ans;}
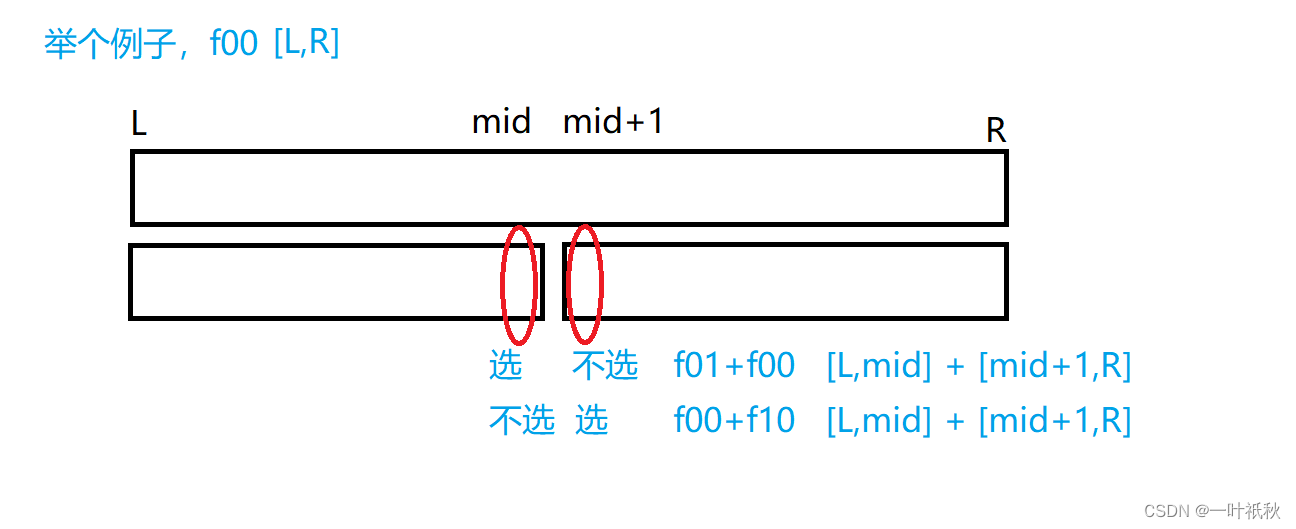
}但是上述做法会超时,需要换一种做法,这题实际上需要使用线段树动态维护[0,n-1]的最大值,就是将 [l,r] = [l,mid] + [mid+1,r],不断的分治,但是由于题目要求不包含相邻元素,也就是说mid 和 mid+1这两个点最多只能取一个,而只靠一维数组无法维护,所以需要一个二维数组f[n][4],这里先用f00,f01,f10,f11表示一下它们的状态:
- f00:表示[l,r]l,r都不选的合法最大值
- f01:表示[l,r]l不选的合法最大值(r可选可不选)
- f10:表示[l,r]r不选的合法最大值(l可选可不选)
- f11:表示[l,r]都可以选的合法最大值(l,r可选可不选)
它们之间的递推关系:
- f00 = max(f01+f00, f00+f10)
- f01 = max(f00+f11, f01+f01)
- f10 = max(f10+f10, f11+f00)
- f11 = max(f10+f11, f11+f01)
画个图来理解一下:
剩下的基本都是线段树基本方法,没什么变化,代码如下:
class Solution {//f00:表示[l,r]l,r都不选的合法最大值//f01:表示[l,r]l不选的合法最大值(r可选可不选)//f10:表示[l,r]r不选的合法最大值(l可选可不选)//f11:表示[l,r]都可以选的合法最大值(l,r可选可不选)//[l, r] = [l, mid] + [mid+1, r]// 00 01 10 11//f00 = max(f01+f00, f00+f10)//f01 = max(f00+f11, f01+f01)//f10 = max(f10+f10, f11+f00)//f11 = max(f10+f11, f11+f01)int[][] f;int[] a;void maintain(int i){f[i][0] = Math.max(f[i<<1][1]+f[i<<1|1][0], f[i<<1][0]+f[i<<1|1][2]);f[i][1] = Math.max(f[i<<1][0]+f[i<<1|1][3], f[i<<1][1]+f[i<<1|1][1]);f[i][2] = Math.max(f[i<<1][2]+f[i<<1|1][2], f[i<<1][3]+f[i<<1|1][0]);f[i][3] = Math.max(f[i<<1][2]+f[i<<1|1][3], f[i<<1][3]+f[i<<1|1][1]);}void build(int l, int r, int i){if(l == r){f[i][3] = Math.max(0, a[l]);}else{int mid = (l + r) / 2;build(l, mid, i<<1);build(mid+1, r, i<<1|1);maintain(i);}}void update(int l, int r, int i, int R, int val){if(l == r){f[i][3] = Math.max(0, val);return;} int mid = (l + r) / 2;if(R <= mid){update(l, mid, i<<1, R, val);}else{update(mid+1, r, i<<1|1, R, val);}maintain(i);}int query(int l, int r, int i){return f[i][3];}public int maximumSumSubsequence(int[] nums, int[][] queries) {int MOD = (int)1e9 + 7;int n = nums.length;f = new int[n<<2][4];a = nums;build(0, n-1, 1);int ans = 0;for(int[] q : queries){update(0, n-1, 1, q[0], q[1]);ans = (ans + query(0, n-1, 1))%MOD;}return ans%MOD;}
}








![[数据集][目标检测]老鼠检测数据集VOC+YOLO格式4107张1类别](https://img-blog.csdnimg.cn/direct/9290e202057b41ab83eae6cfd8f50f0e.png)