回溯问题
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
组合是不强调元素顺序的,排列是强调元素顺序。
回溯法**解决的问题都可以抽象为树形结构**
回溯三部曲。
- 回溯函数模板返回值以及参数
在回溯算法中,函数起名字为backtracking,函数返回值一般为void。
再来看一下参数,因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
void backtracking(参数)
- 回溯函数终止条件
既然是树形结构,那么我们在讲解二叉树的递归 (opens new window)的时候,就知道遍历树形结构一定要有终止条件。
所以回溯也有要终止条件。
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {存放结果;return;
}- 回溯搜索的遍历过程
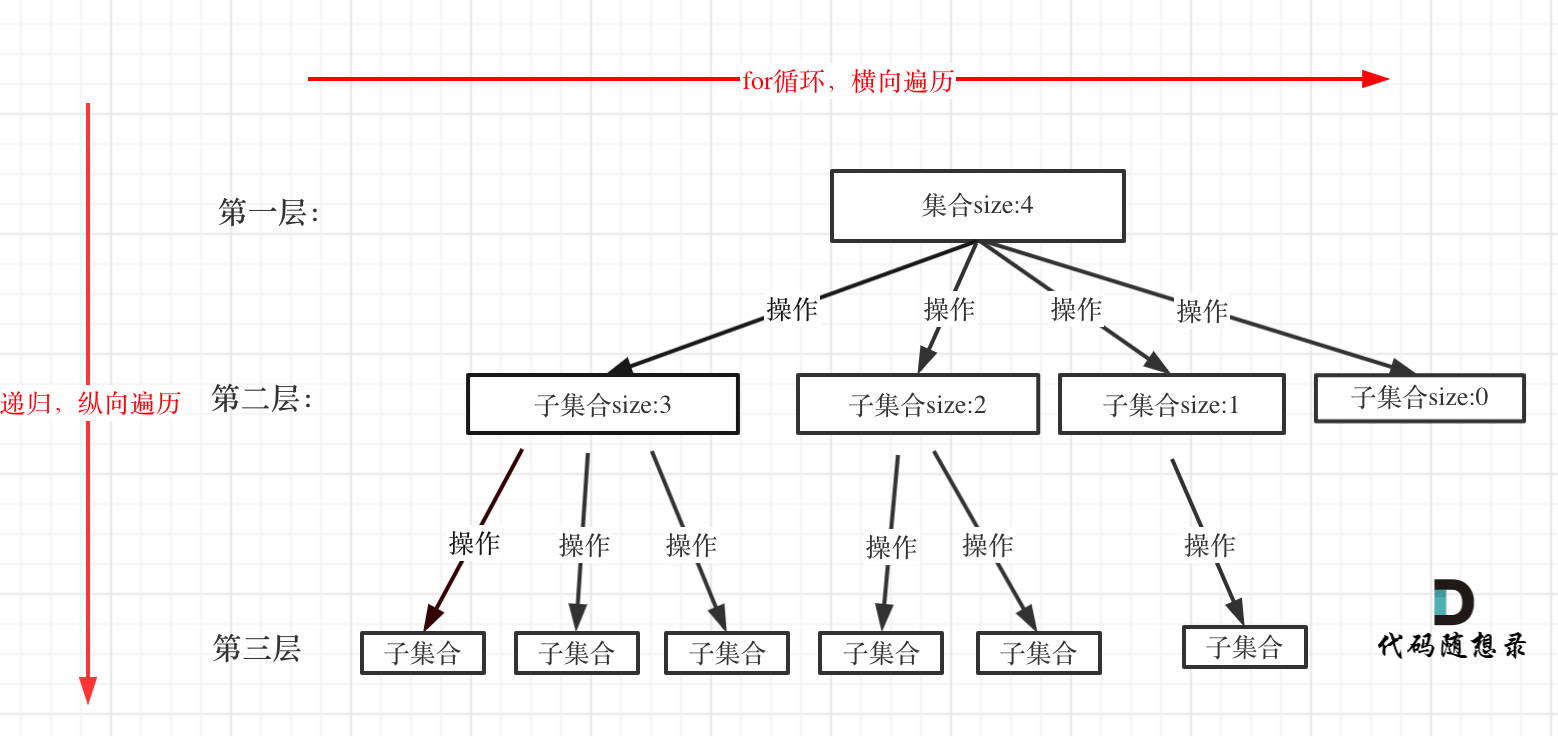
回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归。
大家可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}剪枝精髓是:for循环在寻找起点的时候要有一个范围,如果这个起点到集合终止之间的元素已经不够 题目要求的k个元素了,就没有必要搜索了。
写 backtrack 函数时,需要维护走过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时,将「路径」记入结果集。
回溯算法秒杀所有排列-组合-子集问题
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素,主要有以下几种变体:
形式一、元素无重不可复选,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式。
以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该只有 [7]。
形式二、元素可重不可复选,即 nums 中的元素可以存在重复,每个元素最多只能被使用一次。
以组合为例,如果输入 nums = [2,5,2,1,2],和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
形式三、元素无重可复选,即 nums 中的元素都是唯一的,每个元素可以被使用若干次。
以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该有两种 [2,2,3] 和 [7]。
17 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
理解本题后,要解决如下三个问题:
- 数字和字母如何映射 :map映射
- 两个字母就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来 :回溯算法
- 输入1 * #按键等等异常情况
本题每一个数字代表的是不同集合,也就是求不同集合之间的组合
class Solution {// 每个数字到字母的映射String[] mapping = new String[] {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};List<String> res = new LinkedList<>();public List<String> letterCombinations(String digits) {if (digits.isEmpty()) {return res;}// 从 digits[0] 开始进行回溯backtrack(digits, 0, new StringBuilder());return res;}// 回溯算法主函数void backtrack(String digits, int start, StringBuilder sb) {if (sb.length() == digits.length()) {// 到达回溯树底部res.add(sb.toString());return;}// 回溯算法框架for (int i = start; i < digits.length(); i++) {int digit = digits.charAt(i) - '0';for (char c : mapping[digit].toCharArray()) {// 做选择sb.append(c);// 递归下一层回溯树backtrack(digits, i + 1, sb);// 撤销选择sb.deleteCharAt(sb.length() - 1);}}}78 子集(元素无重不可复选)需要start标记
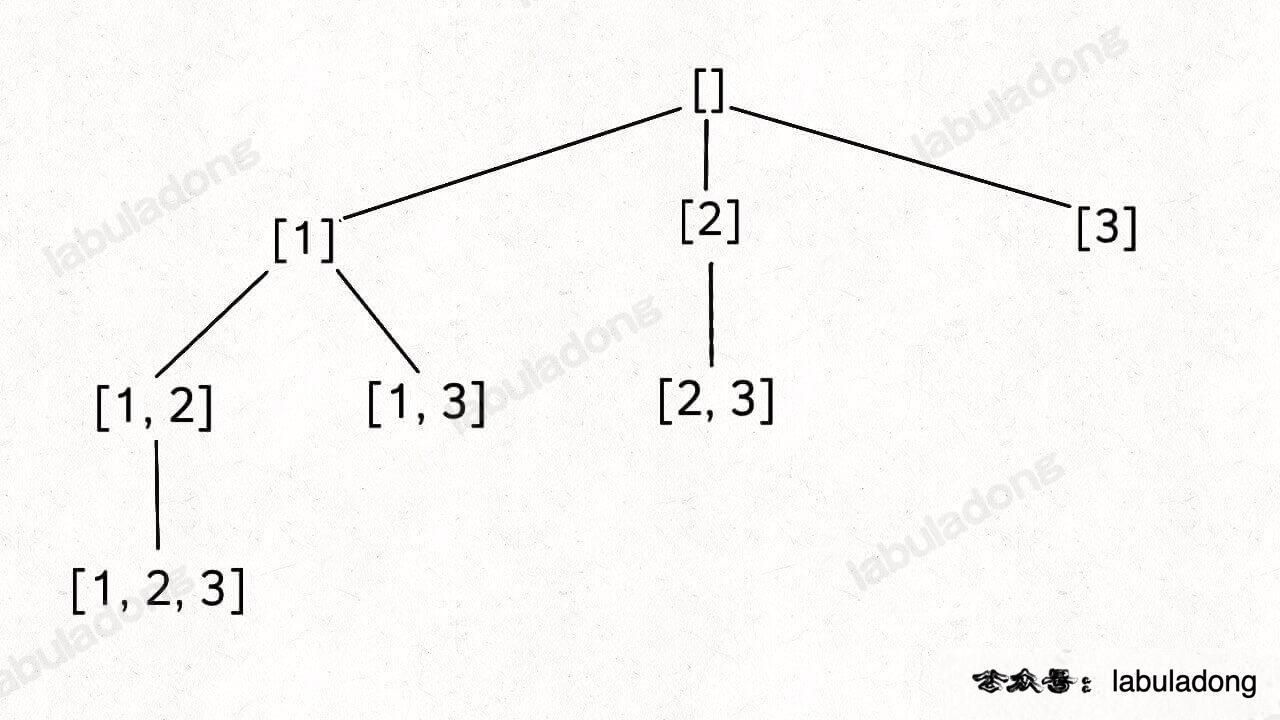
集合中的元素不用考虑顺序,[1,2,3] 中 2 后面只有 3,如果你添加了前面的 1,那么 [2,1] 会和之前已经生成的子集 [1,2] 重复。
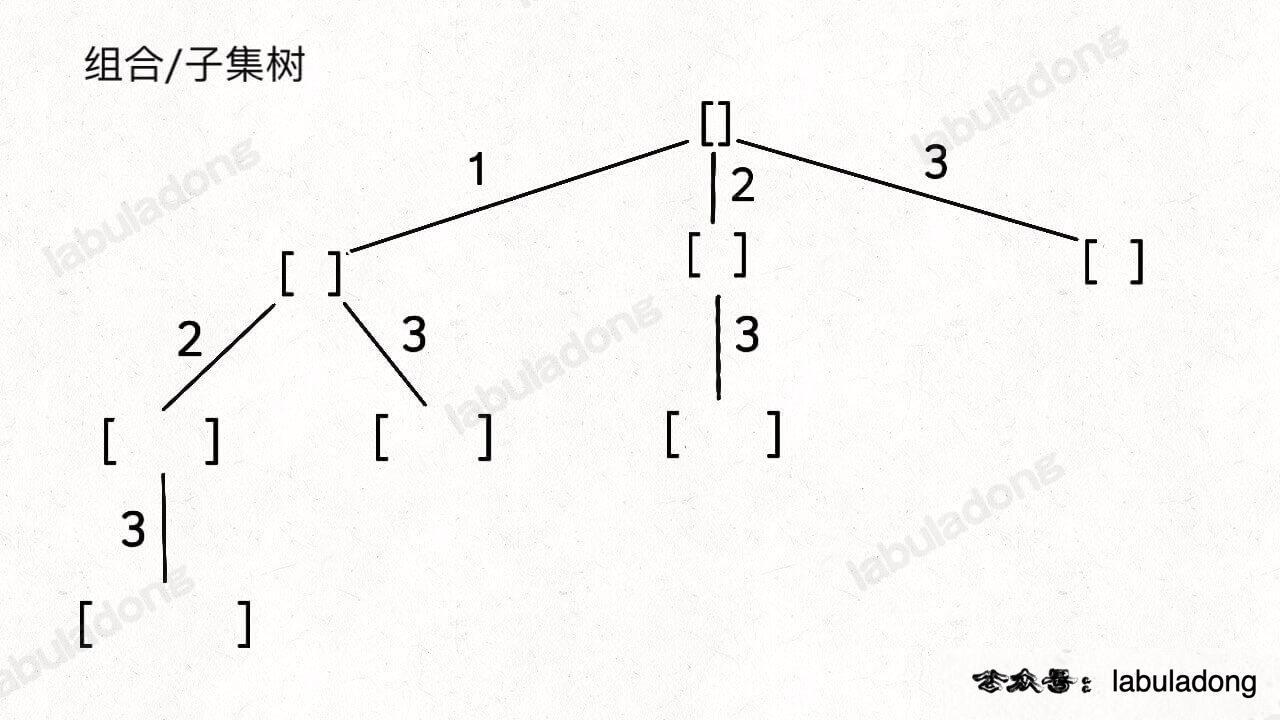
如果把根节点作为第 0 层,将每个节点和根节点之间树枝上的元素作为该节点的值,那么第 n 层的所有节点就是大小为 n 的所有子集。比如大小为 2 的子集就是这一层节点的值。
使用start参数控制树枝的生长避免产生重复的子集,用track记录根节点到每个节点的路径的值,同时在前序位置把每个节点的路径值收集起来,完成回溯树的遍历就收集了所有子集
base case:
当 start == nums.length 时,叶子节点的值会被装入 res,但 for 循环不会执行,也就结束了递归。
class Solution {List<List<Integer>> res = new LinkedList<>();// 记录回溯算法的递归路径LinkedList<Integer> track = new LinkedList<>();// 主函数public List<List<Integer>> subsets(int[] nums) {backtrack(nums, 0);return res;}// 回溯算法核心函数,遍历子集问题的回溯树void backtrack(int[] nums, int start) {//base case//当 start == nums.length 时,叶子节点的值会被装入 res,但 for 循环不会执行,也就结束了递归。// 前序位置,每个节点的值都是一个子集res.add(new LinkedList<>(track));// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 做选择track.addLast(nums[i]);// 通过 start 参数控制树枝的遍历,避免产生重复的子集backtrack(nums, i + 1);// 撤销选择track.removeLast();}}
}77 组合(元素无重不可复选)
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
组合和子集是一样的:大小为 k 的组合就是大小为 k 的子集。
class Solution {List<List<Integer>> res = new LinkedList<>();// 记录回溯算法的递归路径LinkedList<Integer> track = new LinkedList<>();// 主函数public List<List<Integer>> combine(int n, int k) {backtrack(1, n, k);return res;}// 回溯算法核心函数,遍历子集问题的回溯树void backtrack(int start, int n, int k) {// base caseif (k == track.size()) {res.add(new LinkedList<>(track));return;}// 回溯算法标准框架for (int i = start; i <= n; i++) {// 做选择track.addLast(i);// 通过 start 参数控制树枝的遍历,避免产生重复的子集backtrack(i + 1, n, k);// 撤销选择track.removeLast();}}
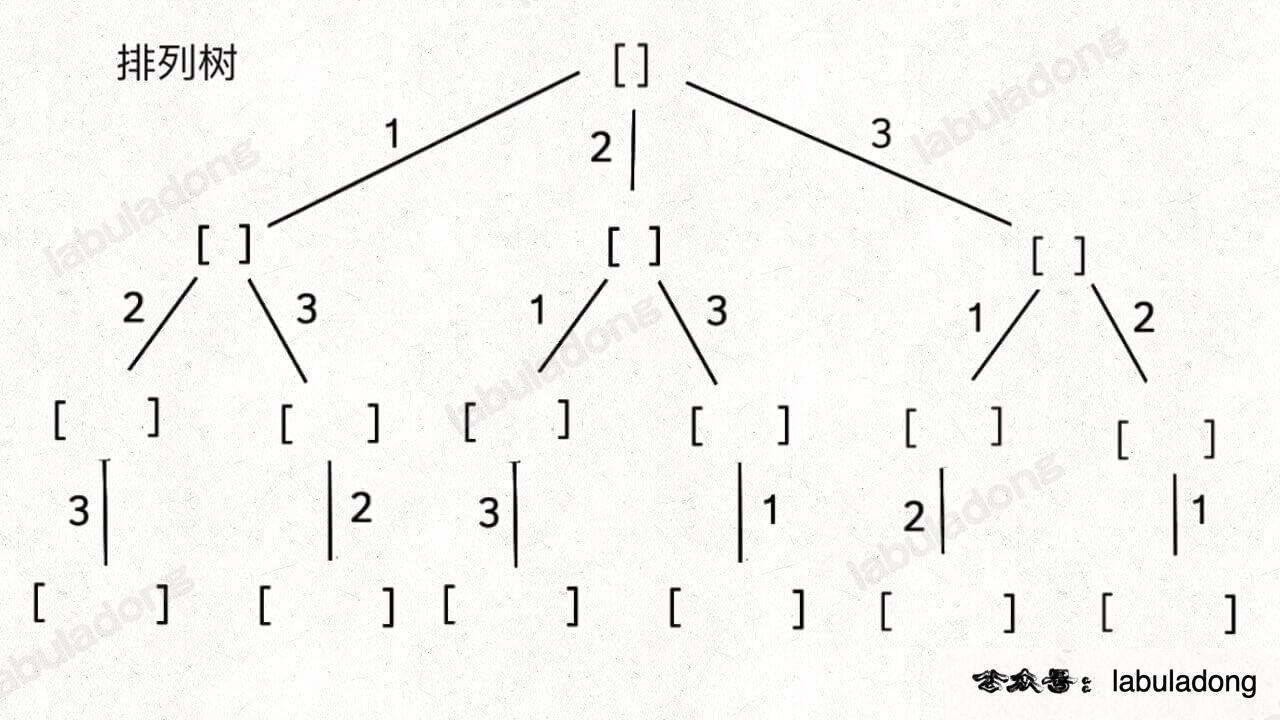
}全排列(元素无重不可复选)使用 used数组标记剩余可选择元素
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
刚才讲的组合/子集问题使用 start 变量保证元素 nums[start] 之后只会出现 nums[start+1..] 中的元素,通过固定元素的相对位置保证不出现重复的子集。
但排列问题本身就是让你穷举元素的位置,nums[i] 之后也可以出现 nums[i] 左边的元素,所以之前的那一套玩不转了,需要额外使用 used 数组来标记哪些元素还可以被选择。
class Solution {
//全局变量List<List<Integer>> res = new LinkedList<>();LinkedList<Integer> track = new LinkedList<>();/* 主函数,输入一组不重复的数字,返回它们的全排列 */List<List<Integer>> permute(int[] nums) {// 「路径」中的元素会被标记为 true,避免重复使用boolean[] used = new boolean[nums.length];backtrack(nums, used);return res;}// 路径:记录在 track 中// 选择列表:nums 中不存在于 track 的那些元素(used[i] 为 false)// 结束条件:nums 中的元素全都在 track 中出现void backtrack(int[] nums ,boolean[] used) {// 触发结束条件if (track.size() == nums.length) {res.add(new LinkedList(track));return;}for (int i = 0; i < nums.length; i++) {// 排除不合法的选择if (used[i]) {// nums[i] 已经在 track 中,跳过 使用过就不再使用 全排列问题不包含重复的数字continue;}// 做选择track.add(nums[i]);used[i] = true;// 进入下一层决策树backtrack(nums, used);// 取消选择track.removeLast();used[i] = false;}}
}如果题目不让你算全排列,而是让你算元素个数为 k 的排列,怎么算?
也很简单,改下 backtrack 函数的 base case,仅收集第 k 层的节点值即可:
// 回溯算法核心函数
void backtrack(int[] nums, int k) {// base case,到达第 k 层,收集节点的值if (track.size() == k) {// 第 k 层节点的值就是大小为 k 的排列res.add(new LinkedList(track));return;}// 回溯算法标准框架for (int i = 0; i < nums.length; i++) {// ...backtrack(nums, k);// ...}
}子集 II (元素可重<需要剪枝> 不可复选)
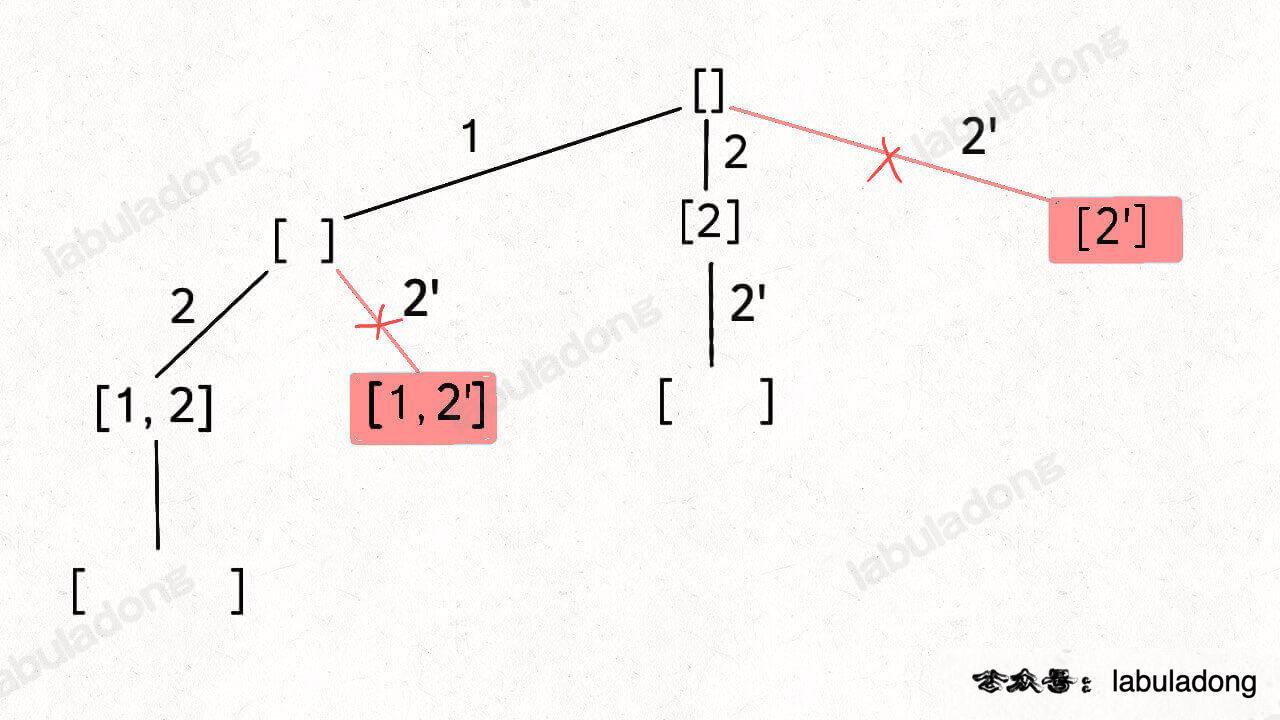
[2] 和 [1,2] 这两个结果出现了重复,所以我们需要进行剪枝,如果一个节点有多条值相同的树枝相邻,则只遍历第一条,剩下的都剪掉,不要去遍历
体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现 nums[i] == nums[i-1],则跳过
这段代码和之前标准的子集问题的代码几乎相同,就是添加了排序和**剪枝的逻辑**
class Solution {List<List<Integer>> res = new LinkedList<>();LinkedList<Integer> track = new LinkedList<>();public List<List<Integer>> subsetsWithDup(int[] nums) {// 先排序,让相同的元素靠在一起Arrays.sort(nums);backtrack(nums, 0);return res;}void backtrack(int[] nums, int start) {// 前序位置,每个节点的值都是一个子集res.add(new LinkedList<>(track));for (int i = start; i < nums.length; i++) {// 剪枝逻辑,值相同的相邻树枝,只遍历第一条if (i > start && nums[i] == nums[i - 1]) {continue;}track.addLast(nums[i]);backtrack(nums, i + 1);track.removeLast();}}
}组合总和 II (元素可重<需要剪枝> 不可复选)
组合问题和子集问题是等价的
只要额外用一个 trackSum 变量记录回溯路径上的元素和,然后将 base case 改一改即可解决这道题:
class Solution {List<List<Integer>> res = new LinkedList<>();// 记录回溯的路径LinkedList<Integer> track = new LinkedList<>();// 记录 track 中的元素之和int trackSum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {if (candidates.length == 0) {return res;}// 先排序,让相同的元素靠在一起Arrays.sort(candidates);backtrack(candidates, 0, target);return res;}// 回溯算法主函数void backtrack(int[] nums, int start, int target) {// base case,达到目标和,找到符合条件的组合if (trackSum == target) {res.add(new LinkedList<>(track));return;}// base case,超过目标和,直接结束if (trackSum > target) {return;}// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 剪枝逻辑,值相同的树枝,只遍历第一条if (i > start && nums[i] == nums[i - 1]) {continue;}// 做选择track.add(nums[i]);trackSum += nums[i];backtrack(nums, i + 1, target);track.removeLast();trackSum -= nums[i]; //新增变量也要回溯}}
}全排列 II(元素可重<需要剪枝>不可复选)
对比一下之前的标准全排列解法代码,这段解法代码只有两处不同:
1、对 nums 进行了排序。
2、添加了一句额外的剪枝逻辑。
标准全排列算法之所以出现重复,是因为把相同元素形成的排列序列视为不同的序列,但实际上它们应该是相同的;而如果固定相同元素形成的序列顺序,当然就避免了重复。
class Solution {List<List<Integer>> res = new LinkedList<>();LinkedList<Integer> track = new LinkedList<>();boolean[] used;public List<List<Integer>> permuteUnique(int[] nums) {// 先排序,让相同的元素靠在一起Arrays.sort(nums);used = new boolean[nums.length];backtrack(nums);return res;}void backtrack(int[] nums) {if (track.size() == nums.length) {res.add(new LinkedList(track));return;}for (int i = 0; i < nums.length; i++) {if (used[i]) {continue;}// 新添加的剪枝逻辑,固定相同的元素在排列中的相对位置if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue; //i-1没使用过}track.add(nums[i]);used[i] = true;backtrack(nums);track.removeLast();used[i] = false;}}
}组合总和(元素无重 可复选)
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
需要startIndex来控制for循环的起始位置,对于组合问题,什么时候需要startIndex呢?
我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:77.组合 (opens new window),216.组合总和III (opens new window)。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:17.电话号码的字母组合
这道题说是组合问题,实际上也是子集问题:candidates 的哪些子集的和为 target?
标准的子集/组合问题是如何保证不重复使用元素的?
答案在于 backtrack 递归时输入的参数 start,这个 i 从 start 开始,那么下一层回溯树就是从 start`` ``+ 1 开始,从而保证 nums[start] 这个元素不会被重复使用:
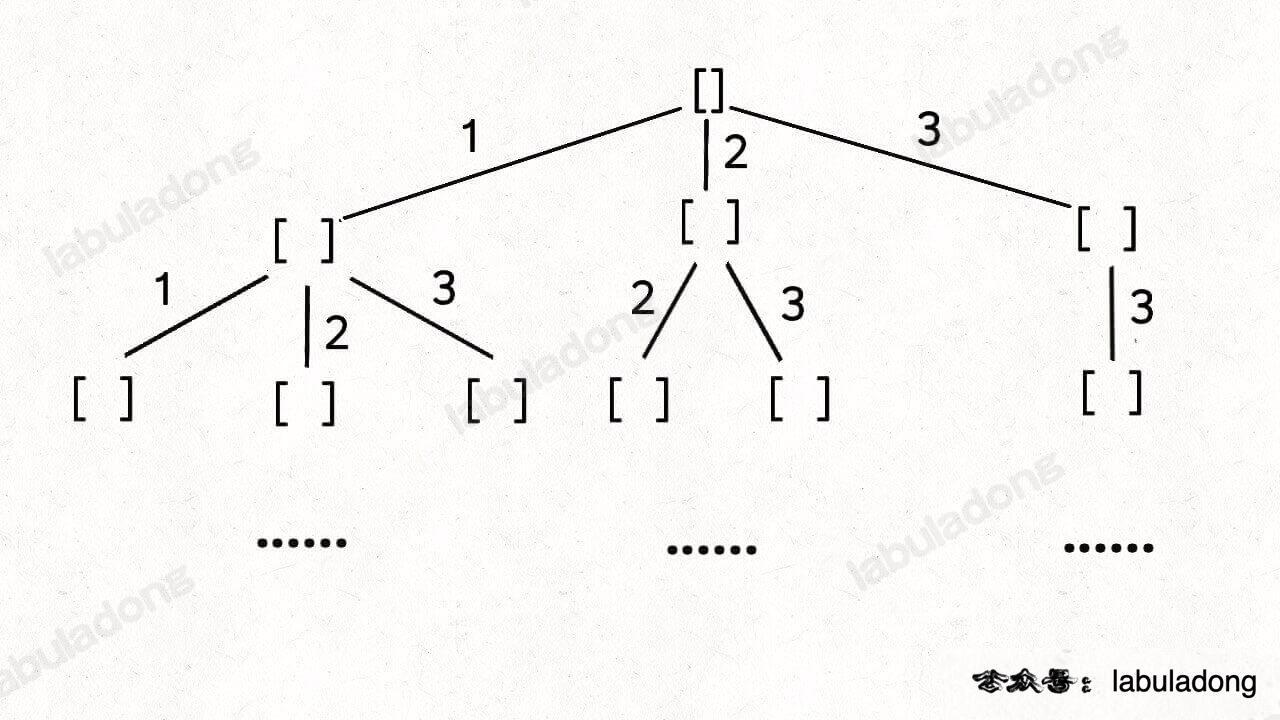
如果我想让每个元素被重复使用,我只要把 i + 1 改成 i 即可
当然,这样这棵回溯树会永远生长下去,所以我们的递归函数需要设置合适的 base case 以结束算法,即路径和大于 target 时就没必要再遍历下去了。
class Solution {List<List<Integer>> res = new LinkedList<>();// 记录回溯的路径LinkedList<Integer> track = new LinkedList<>();// 记录 track 中的路径和int trackSum = 0;public List<List<Integer>> combinationSum(int[] candidates, int target) {if (candidates.length == 0) {return res;}backtrack(candidates, 0, target);return res;}// 回溯算法主函数void backtrack(int[] nums, int start, int target) {// base case,找到目标和,记录结果if (trackSum == target) {res.add(new LinkedList<>(track));return;}// base case,超过目标和,停止向下遍历if (trackSum > target) {return;}// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 选择 nums[i]trackSum += nums[i];track.add(nums[i]);// 递归遍历下一层回溯树// 同一元素可重复使用,注意参数 不使用i+1backtrack(nums, i, target);// 撤销选择 nums[i]trackSum -= nums[i];track.removeLast();}}
}排列(元素无重可复选)
标准的全排列算法利用 used 数组进行剪枝,避免重复使用同一个元素。如果允许重复使用元素的话,直接放飞自我,去除所有 used 数组的剪枝逻辑就行了。
class Solution {List<List<Integer>> res = new LinkedList<>();LinkedList<Integer> track = new LinkedList<>();public List<List<Integer>> permuteRepeat(int[] nums) {backtrack(nums);return res;}// 回溯算法核心函数void backtrack(int[] nums) {// base case,到达叶子节点if (track.size() == nums.length) {// 收集叶子节点上的值res.add(new LinkedList(track));return;}// 回溯算法标准框架for (int i = 0; i < nums.length; i++) {// 做选择track.add(nums[i]);// 进入下一层回溯树backtrack(nums);// 取消选择track.removeLast();}}
}最后总结
来回顾一下排列/组合/子集问题的三种形式在代码上的区别。
由于子集问题和组合问题本质上是一样的,无非就是 base case 有一些区别,所以把这两个问题放在一起看。
形式一、元素无重不可复选,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,backtrack 核心代码如下:
/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 做选择track.addLast(nums[i]);// 注意参数backtrack(nums, i + 1);// 撤销选择track.removeLast();}
}/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 剪枝逻辑if (used[i]) {continue;}// 做选择used[i] = true;track.addLast(nums[i]);backtrack(nums);// 撤销选择track.removeLast();used[i] = false;}
}形式二、元素可重不可复选,即 nums 中的元素可以存在重复,每个元素最多只能被使用一次,其关键在于排序和剪枝,backtrack 核心代码如下:
Arrays.sort(nums);
/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 剪枝逻辑,跳过值相同的相邻树枝if (i > start && nums[i] == nums[i - 1]) {continue;}// 做选择track.addLast(nums[i]);// 注意参数backtrack(nums, i + 1);// 撤销选择track.removeLast();}
}Arrays.sort(nums);
/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 剪枝逻辑if (used[i]) {continue;}// 剪枝逻辑,固定相同的元素在排列中的相对位置if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue;}// 做选择used[i] = true;track.addLast(nums[i]);backtrack(nums);// 撤销选择track.removeLast();used[i] = false;}
}形式三、元素无重可复选,即 nums 中的元素都是唯一的,每个元素可以被使用若干次,只要删掉去重逻辑即可,backtrack 核心代码如下:
/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {// 回溯算法标准框架for (int i = start; i < nums.length; i++) {// 做选择track.addLast(nums[i]);// 注意参数backtrack(nums, i);// 撤销选择track.removeLast();}
}/* 排列问题回溯算法框架 */ //删除used逻辑
void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 做选择track.addLast(nums[i]);backtrack(nums);// 撤销选择track.removeLast();}
}部分图引自代码随想录等