一、二分查找法原理介绍
二分查找是经典的查找算法之一,其原理也非常简单。
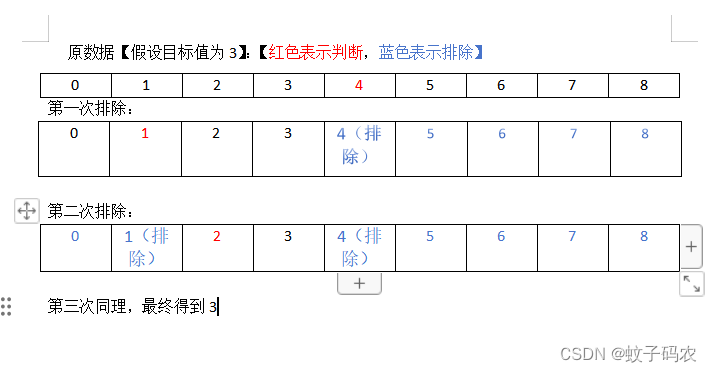
对于已排序的数组(假设是整型,如果非整型,如果有排序和大小比较的定义,也可以使用二分查找),我们每次判断中间值与目标值的大小,从而排除另外半边。
如下图所示,我们每次可以排除现有数组的一半及以上数据,也就是说,二分查找,利用了排除的原理。
二、二分查找的3个关键数据
left:确定左边界,比如上图原数据的0。
right:确定右边界,比如上图原数据的8。(有些题解,会用9表示,则right仍是右边界,只是此边界无法取到)
middle:从中间开始判断,每次排除左边或右边的所有数据。
三、left、right的取值条件
在此先说明一个重点:
left、right是限定数组的,每一次排除元素,都要保证得到的新数组,没有重复、缺失。【缺失可能出错,重复会导致复杂情况】
缺失的情况其实一般不会出现。
我们疑虑的,主要是这个问题:
当 middle > 目标值时, 排除右边区域,那么:
right = middle,还是
right = middle - 1呢?
如果用 right = middle,因为有重复数据,会不会更加保险呢?
别急,接着往下看。
四、二分查找边界值处理【关键是,仅1个元素的数组】
抽象left、right的选值,因为这并非重点,如果明白边界值处理,就能理解left、right选值和while循环条件的原理。
第一,空数组【】
假设我们有一个空数组,必定无所需元素,所以直接返回null。
第二,1元素数组【a】
假设数组中,只有一个元素a,此时只要判断a==目标值否,就能知道数组中是否有值。
第三,其它情况。
我们已知left、right是限定数组的,那么,如果目前数组的中心值middle,刚好等于目标值,就能返回答案。【这是最简单的情况,而且不用考虑1、2情况】
但是常常会出现的问题是:
1.数组中没有目标值。
2.很可能一直迭代到left==right,或者left+1=right时,才得到目标值。【而第2个情况,又得从while条件里,找正确与否。】
不考虑 left+2 == right ,或者 left+3 == right 的原因
left+2 == right:中间值middle,可以等于
( left + right ) / 2 比如【1,4,6】
无论排除左边,还是右边,最后都剩下1元素数组【1】或者【6】
left+3 == right : 中间值middle,为
left+1【(left+left+3)除以2,化简】 比如【1, 4, 6, 9】
那么,左边排除后,剩下【6,9】,即新问题【 left+1 == right 】的解决。
右边排除后,剩下【1】,即为单元素问题。
我们忽略第1个问题,因为如果解决了第2个问题,第1个问题也是迎刃而解。
考虑2种情况, left == right,和 left+1 == right
正如“第二,1元素数组【a】”所说,只要判断中间值 middle == (left+right)/2 == left与目标值的关系,就能知道数组中有无目标值。
我们统一一种算法【满足开头所说的重点】:
1. middle大于目标值,则舍弃右边,所以 right = middle - 1;
2. middle小于目标值,则舍弃左边,所以 left = middle + 1;
3. middle = (left + right) /2;
这种算法可行吗?
显然,当 left 恰好为 right 时,middle正好等于 left,恰好可以判断。
所以,在单元素中满足。
对于 left +1 == right呢?
假设我们刚进入这个数组,那么 middle = left 【 ( left+left+1 ) / 2 】
那么,经过判断,要不就说明 middle > 目标值,数组中无目标值。
要不就是, middle < 目标值,判断右边的最后1个元素。
这一步结束后,结果即1元素数组【a】的解法(或者成功判断)
所以,本题满足。
五、while的循环条件
我们已经了解left、right的取值,最后的重点是,while条件该如何处理?
其实一般都知道,left < right 时,一般都可以继续执行,可是 left == right 时,该怎么办呢?
结合上面的思路,其实一下就能看出来,如果 left == right, 不就恰好是 1元素的数组吗?
那用 left <= right 作为循环条件,会不会无限循环呢?
不会,因为我们把middle也排除了,做到了无重复,所以这个问题不算复杂。
六、异常处理
考虑异常。
数组元素重复
最经典的,就是每一次比较middle后,使:
left = middle;
right = middle;
出现的两种情况:
假设现在有 1元素数组【a】。
middle、left、right都指向a,无论a比目标值大、小,只要不等于,那么left、right会永远指向a,陷入死循环。
当然,也有的情况是 2元素数组【a,b】
left指向a, right指向b,此时middle指向a。
并且,a比目标值小。
此时,left = middle。
而middle又是 left+right的二分之一,恰好是left,又是死循环。
解决:
特地判断 left == right, 和 left+1 == right两种情况。【那么代码就不够简洁,反而复杂了。】
循环条件异常:
对于 left初值为0, right初值为len-1。
如果条件是 left < right ,明显会缺失数据。【不再解释】
如果right初值为len呢?
这是常常出现的问题,此时我们可以发现,right指向空元素。
为了保持数据结构的统一性,必须在接下来的更新里,使得right永远指向空元素【不一定是无值,但是要使 right 指向的区间,已经被排除过。】
这时,在排除时,就可以:
right = middle。
那么循环条件也明显了,如果 left <= right,那么在最后,一定会出现面对 空集合 ,却一直判断的情况。【注:空集合是我们更新后,新数组为null, 而在原数组中,(left+right )/2指向的元素,仍然有值】
七、结语
总之,一定要做好 数组 更新的一致性,做好了这个,就能解题了。
我是蚊子码农,如有补充或者疑问,欢迎在评论区留言。个人的知识体系可能没有那么完善,希望各位多多指正,谢谢大家。