20240531-时间复杂度

1、消失的数字

方法一：位运算

两个数字一样的数组，其中一个数组中少了一个数字，定义一个变量分别异或两个数组，结果即为缺少的数字

    class Solution {public int missingNumber(int[] nums) {int xor = 0;int n = nums.length;//获取数组长度for (int i = 0; i < n; i++) {//因为该数组少一个数，所以i < nxor ^= nums[i];}for (int i = 0; i <= n; i++) {//假设该数组数字为0~n，不少数字，所以i <= nxor ^= i;}//分别遍历两数组进行异或操作，相同数字异或得零//其他数字均出现两次，只有一个数字出现一次return xor;}}

方法二：数学规律

1到n的等差数列的总和，减去当前数组元素的总和，即为缺少的数字

class Solution {public int missingNumber(int[] nums) {int n = nums.length;//等差数列总和 = （首项 + 尾项）* 项数 / 2int total = (1 + n) * n / 2;//当前数组的总和int sum = 0;for(int i=0;i<n;i++){sum += nums[i];}//缺少值 = 等差数列总和 - 数组总和return total - sum;}
}

 2、旋转数组

这个不会，暂且搁置

3、给定一个整数sum，从有N个有序元素的数组中寻找元素a，b，使得a+b的结果最接近sum，最快的平均时间复杂度是（   ）

A.O(n)

B.O(n^2)

C.O(nlogn)

D.O(logn)

选B了

解析：

正确答案A，数组元素有序，所以a，b两个数可以分别从开始和结尾处开始搜索，根据首位元素的和是否大于sum，决定搜索的移动，整个数组被搜索一遍，就可以得到结果，所以时间复杂度为O(n)

4、设某算法的递推公式是T(n)=T(n-1)+n，T(0)=1，则求该算法中第n项的时间复杂度为（）

A.O(n)

B.O(n^2)

C.O(nlogn)

D.O(logn)

解析：

5、分析以下函数的时间复杂度

void fun(int n) {int i=l;while(i<=n)i=i*2;
}

A.O(n)

B.O(n^2)

C.O(nlogn)

D.O(logn)

解析：

D，此函数有一个循环，但是循环没有被执行n次，i 每次都是2倍进行递增，所以只会被执行

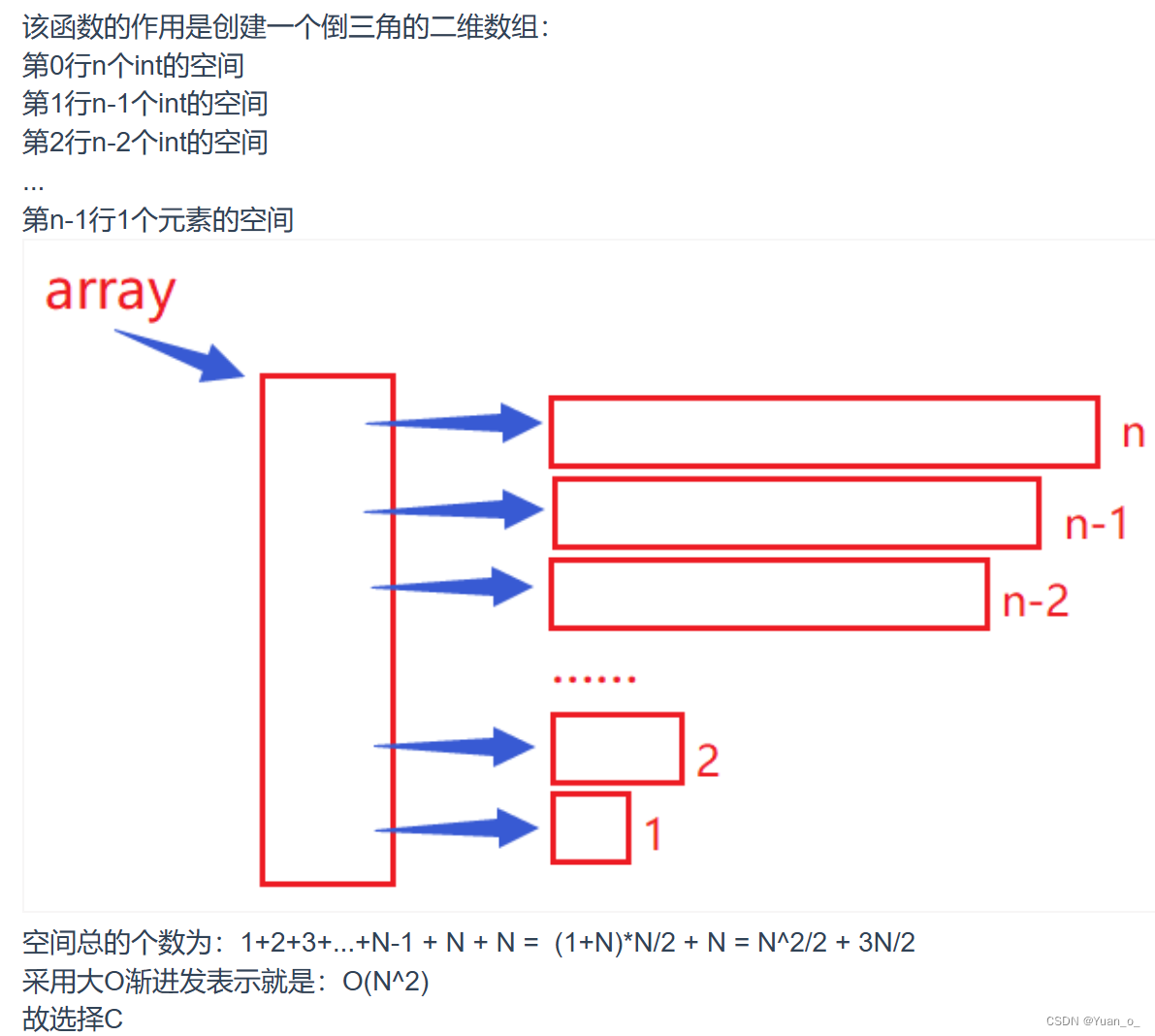
6、分析以下函数的空间复杂度

public static int[][] get2Array(int n){int[][] array = new int[n][];for(int i = 0; i < n; i++) {array[i] = new int[n-i];n--;}return array;
}

A.O(1)

B.O(N)

C.O(N^2)

D.O(logN)

解析：