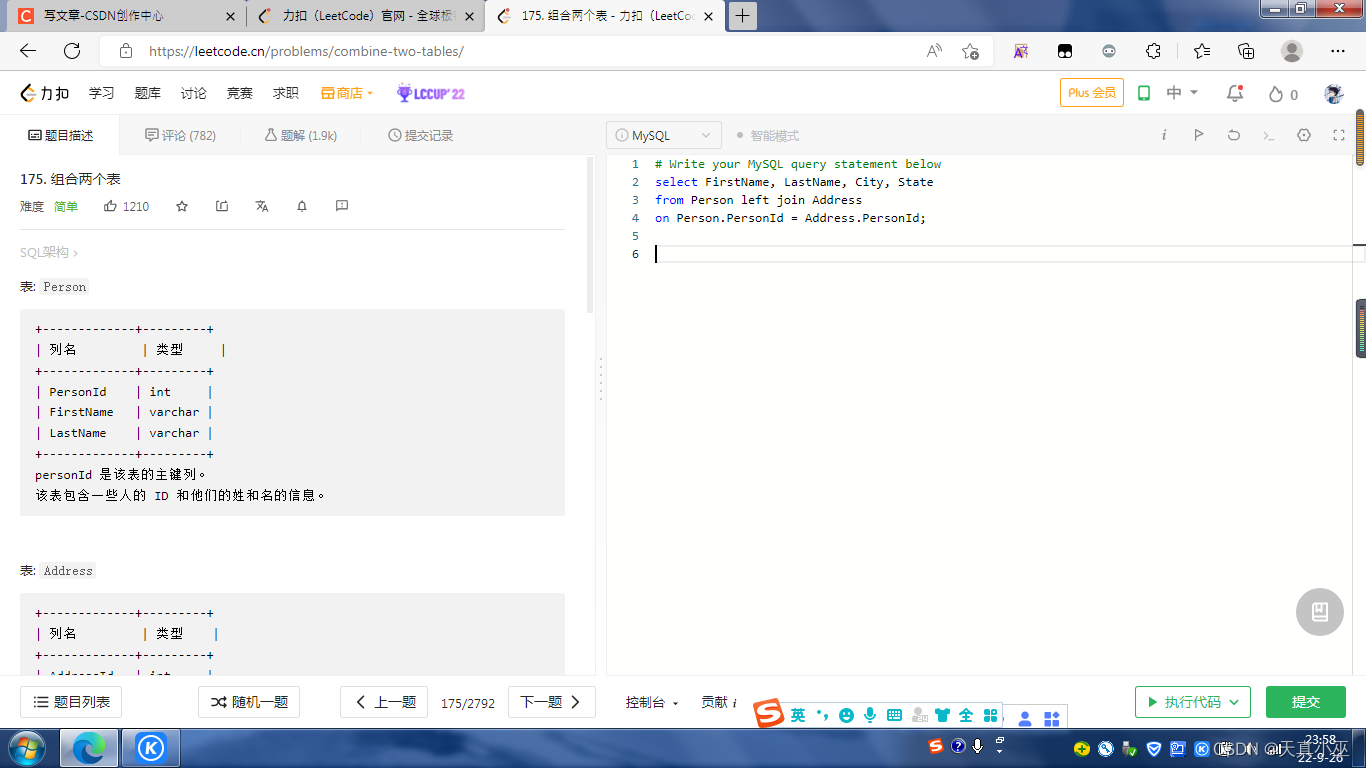
法线贴图
法线贴图分两种,一种是模型空间中的,一种是切线空间中的

模型空间中的法线贴图的rgb代表着每个渲染像素法线的xyz,与顶点坐标处于一个空间,图片是五颜六色的。

切线空间中的法线贴图的rgb同样对应xyz,是切线空间里的坐标,切线空间里的z轴正向垂直与当前三角形便宜,x是当前三角形片元表面的一个切线,y是他们的叉积。
切线空间每个轴范围是-1到1.但图片本身0-255对应的是0-1.而多数法线都是都是(0,0,1)(即当前像素的法向量刚好就是当前片元的顶点法向量)转换到颜色空间就是(0.5,0.5,1)(法向量坐标可能为负,但颜色范围始终为正)。因此图片主要是蓝紫色
两个完全一样材质的物体,由于位置不同光照也会不同。如果用模型空间存储的法线贴图,是绝对法线,法向量会完全不同,无法使用同一张物体。而切线空间存储的法线贴图完全是基于物体自身的,是相对法线,多个物体可以复用(优点)。但再实际计算时,需要根据物体本身的缩放位移做相应的矩阵转换处理(缺点)
模型空间的法线贴图直接提取向量信息做为法线向量即可
Vec3f Model::getNormal(float x, float y) {TGAColor n = normalTex_.get(x * normalTex_.get_width(), y * normalTex_.get_height());Vec3f res;for (int i = 0; i < 3; i++) {res[i] = n.bgra[i] / 255.f * 2 - 1.f;}return res;
}
//....
struct normalTexShader :public IShader {mat<2, 3, float> uv;virtual Vec4f vertex(int iface, int vertIdx, Matrix mvp) {Vec3f v = model->vert(model->face(iface)[vertIdx]);uv.set_col(vertIdx, model->tverts(model->tface(iface)[vertIdx]));return mvp * embed<4>(v);}virtual bool fragment(Vec3f barycentricCoordinates, TGAColor& color) {Vec2f texcoords = uv * barycentricCoordinates;Vec3f normal = model->getNormal(texcoords.x, texcoords.y);float I = std::max(0.f, normal * light_dir);color = model->getDiffuseColor(texcoords.x, texcoords.y) * I;return false;}
};

切线空间的法线贴图使用,重点求出tbn矩阵,将切线空间的法线转化到世界空间中
tbn矩阵
tbn矩阵
tbn矩阵
当tbn矩阵的n是模型空间时,法线贴图取值经过tbn变换后是模型空间法线
当tbn矩阵的n是世界空间时,法线贴图取值经过tbn变换后是世界空间法线
对于三角形表面所有点,t切线和b切线都是相同的

顶点法线与面法线可能不同
面法线只是垂直于面的一条向量,规定了面的正反,而顶点法线才是用于光照信息的处理(建模软件中,顶点法线的最初是的默认情况也并非是面法线的平均,只有当在建模软件中对物体进行了平滑着色后,才会根据面法线平均得到顶点法线)
因此要通过每个顶点的切线找到曲面的法线
struct Shader :public IShader {mat<2, 3, float> uv;Vec3f vp[3];Matrix MVP = rasterizer->getProjection() * rasterizer->getModelView();mat<3, 3, float> n;virtual Vec4f vertex(int iface, int vertIdx) {Vec3f v = model->vert(model->face(iface)[vertIdx]);uv.set_col(vertIdx, model->tverts(model->tface(iface)[vertIdx]));vp[vertIdx] = v;n.set_col(vertIdx, model->nverts(model->nface(iface)[vertIdx]));return MVP * embed<4>(v);}virtual bool fragment(Vec3f barycentricCoordinates, TGAColor& color) {Vec3f N = (n * barycentricCoordinates).normalize();float u1 = uv[0][1] - uv[0][0];float v1 = uv[1][1] - uv[1][0];float u2 = uv[0][2] - uv[0][0];float v2 = uv[1][2] - uv[1][0];Vec3f e1 = vp[1] - vp[0];Vec3f e2 = vp[2] - vp[0];float f = 1.f / (u1 * v2 - u2 * v1);Vec3f T = (e1 * v2 - e2 * v1) * f;T = T - N * (T * N);T.normalize();Vec3f B = cross(N, T).normalize();mat<3, 3, float> TBN;TBN.set_col(0, T);TBN.set_col(1, B);TBN.set_col(2, N);Vec2f texcoords = uv * barycentricCoordinates;Vec3f normal = TBN * model->getNormal(texcoords.x, texcoords.y);float I = std::max(0.f, normal * light_dir);color = model->getDiffuseColor(texcoords.x, texcoords.y) * I;return false;}
};
有一点注意的是,很多文章里的tbn矩阵只到了这步推导公式
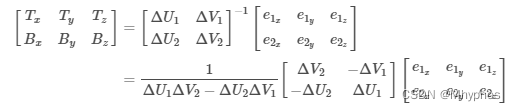
求出了t和b向量后,实际上还要加上N做一次正交化,否则是不保证相互垂直的。最终才是tbn矩阵

项目跟随练习代码地址