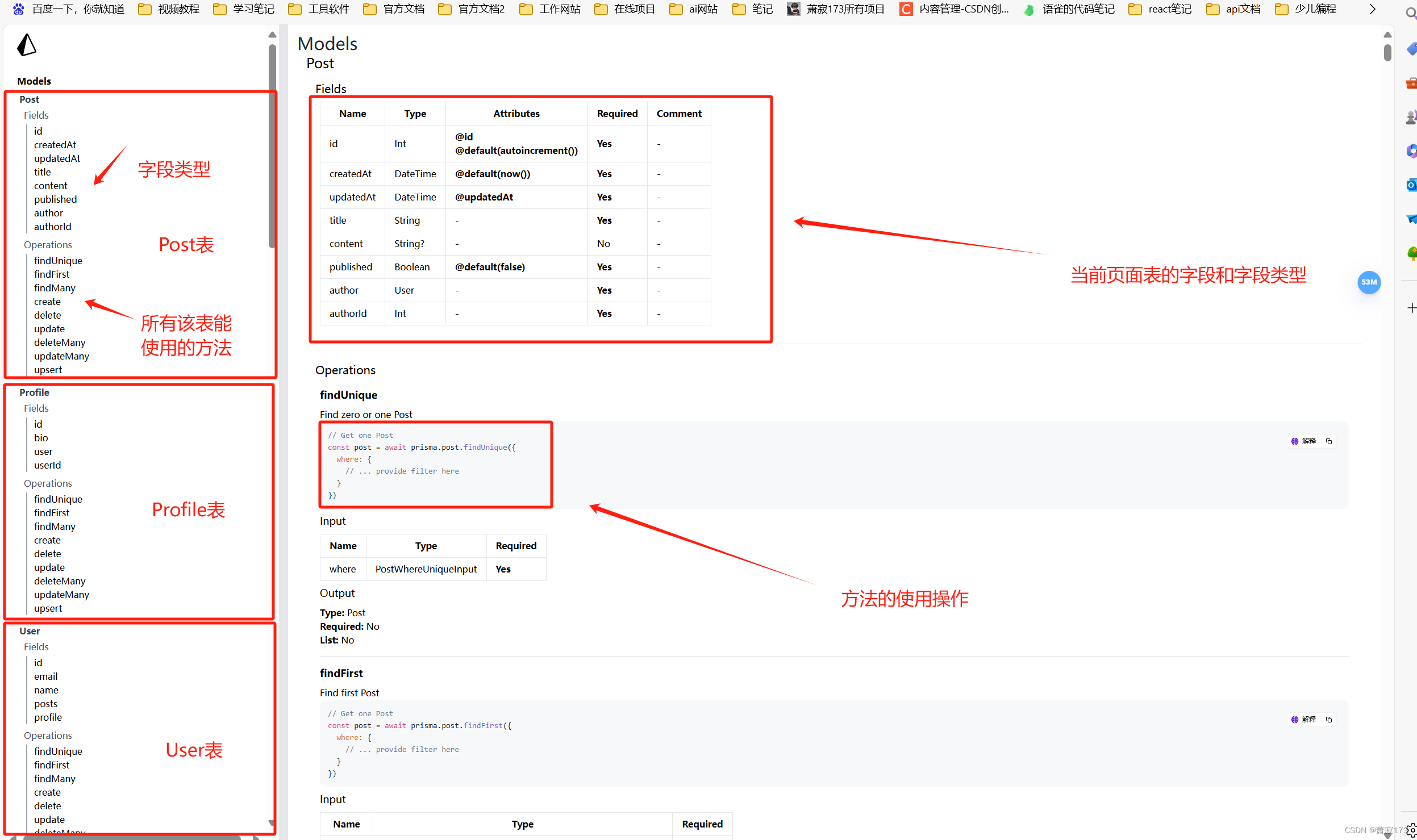
DeepSORT（目标跟踪算法）中自由度决定卡方分布的形状

flyfish

重要的两个点

自由度决定卡方分布的形状（本文）
马氏距离的平方在多维正态分布下服从自由度为 k 的卡方分布

独立的信息

在统计学中，独立的信息是指数据中的独立变量或值的数量。当我们计算样本统计量（如平均值或方差）时，某些数据点的值可以从其他数据点和统计量中推导出来，因此这些点不再提供独立的信息。

卡方分布是一种统计学上的概率分布，通常用于假设检验，比如检验数据的独立性或适合度。卡方分布描述的是一个变量的值如何分布，特别是当这些变量表示方差或者是两个变量之间的独立性时。它的形状取决于自由度（degree of freedom, df），自由度越高，分布越接近正态分布。

绘制几个不同自由度下的卡方分布

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats# 定义自由度
dfs = [1, 2, 3, 5, 10]# 设置x轴范围
x = np.linspace(0, 20, 1000)# 创建图形
plt.figure(figsize=(10, 6))# 绘制不同自由度的卡方分布曲线
for df in dfs:plt.plot(x, stats.chi2.pdf(x, df), label=f'df={df}')# 添加图例和标签
plt.legend()
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Chi-Square Distribution')
plt.grid(True)# 显示图形
plt.show()

在这里插入图片描述
卡方分布图：

df=1：分布最偏，右侧有长尾。
df=2：开始向左侧移动，但仍有右侧长尾。
df=3：分布更集中，右侧长尾减弱。
df=5：分布更靠近正态分布，右侧尾巴更短。
df=10：非常接近正态分布，右侧尾巴很短。
这种图形有助于理解自由度对卡方分布形状的影响。随着自由度增加，卡方分布逐渐向正态分布靠拢。

卡方分布的公式

可以用以下数学表达式来表示：

$\frac{1}{2^{k/2} \Gamma(k/2)} x^{k/2-1} e^{-x/2}$

其中：

$x$ 是卡方变量（取非负值）。
$k$ 是自由度（degrees of freedom）。
$\Gamma$ 是伽玛函数（Gamma function），它是阶乘函数的一种扩展，满足 $\Gamma(n) = (n-1)!$ 对于正整数 $n$ 。

伽玛函数 (Gamma function)

伽玛函数是一种特殊函数，它是阶乘函数在非整数值上的扩展。对于一个正整数 $n$ ，伽玛函数 $\Gamma(n)$ 等于 $(n - 1)!$ 。伽玛函数的定义是：

$\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt$

当 $z$ 是正整数时，伽玛函数满足 $\Gamma(n) = (n-1)!$ 。

通常自由度等于数据点的数量减去你计算中所涉及的参数数量。

例如：

样本的平均值计算：

你有 $n$ 个数据点。
计算平均值需要一个参数（就是这个平均值）。
因此，自由度是 $n - 1$ 。

线性回归：

假设你有 $n$ 个数据点和两个参数（斜率和截距）。
自由度是 $n - 2$ 。

假设我们有5个数据点 $x_1, x_2, x_3, x_4, x_5$ ：

计算平均值：
$\bar{x} = \frac{x_1 + x_2 + x_3 + x_4 + x_5}{5}$
计算每个数据点的偏差（数据点与平均值的差）：
$d_1 = x_1 - \bar{x}$
$d_2 = x_2 - \bar{x}$
$d_3 = x_3 - \bar{x}$
$d_4 = x_4 - \bar{x}$
$d_5 = x_5 - \bar{x}$
偏差的和为零：
$d_1 + d_2 + d_3 + d_4 + d_5 = 0$

这表明，知道了前4个偏差 $d_1, d_2, d_3, d_4$ 后，第5个偏差 $d_5$ 是可以通过前4个偏差计算出来的，因为偏差的总和必须为零：
$d_5 = - (d_1 + d_2 + d_3 + d_4)$

这说明第5个偏差并不是独立的，它依赖于前4个偏差。

自由度的减少

当我们计算平均值时，我们使用了所有数据点的信息，这个平均值本身是由这些数据点计算出来的，因此在计算方差时，有一个数据点的信息量不再是独立的（因为它可以从其他数据点和平均值推导出来）。这就是为什么在计算方差时，自由度是 $n - 1$ 。

无论最后一个数据点是大是小，这个推理过程都成立。因为平均值 $\bar{x}$ 是所有数据点的一个函数，在计算方差时，所有数据点与平均值的偏差和为零：

$\sum_{i=1}^{n} (x_i - \bar{x}) = 0$

这表明，如果你知道 $n - 1$ 个偏差，那么最后一个偏差是可以通过前面 $n - 1$ 个偏差计算出来的。因此，总共有 $n - 1$ 个独立的信息，这就是我们在计算样本方差时为什么使用 $n - 1$ 作为分母。

自由度的作用

调整估计偏差：
使用自由度调整计算可以消除估计过程中的偏差，使得估计结果更加准确。例如，样本方差的计算使用 $n - 1$ 作为分母，使其成为总体方差的无偏估计。
反映数据独立性：
自由度表示数据集中独立信息的数量。在统计计算中，自由度反映了可以自由变动的数据点数量，而不受其他数据点或估计参数的约束。
决定分布形状：
在假设检验中，自由度决定了统计量的分布形状，如卡方分布。不同的自由度会导致分布形状不同，从而影响显著性水平和置信区间的计算。

要深入理解样本方差、总体方差以及无偏估计的概念，首先需要了解一些基础定义和背景知识。让我们逐一解释这些概念。

样本方差、总体方差、无偏估计

总体方差（Population Variance）：
总体方差是描述总体数据的离散程度的度量，表示总体数据点与总体均值之间的平均平方偏差。假设总体中有 $N$ 个数据点 $X_1, X_2, \ldots, X_N$ ，总体方差的计算公式为：
$\sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (X_i - \mu)^2$
其中， $\mu$ 是总体的平均值。

样本方差（Sample Variance）：
样本方差是从样本数据中估计总体方差的度量，表示样本数据点与样本均值之间的平均平方偏差。假设样本中有 $n$ 个数据点 $x_1, x_2, \ldots, x_n$ ，样本方差的计算公式为：
$s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2$
其中， $\bar{x}$ 是样本的平均值。

无偏估计（Unbiased Estimator）

一个估计量是无偏的，如果其期望值等于所要估计的总体参数。即，对于样本方差 $s^2$ 来说，当它作为总体方差 $\sigma^2$ 的估计时，满足以下条件：
$\mathbb{E}[s^2] = \sigma^2$
其中， $\mathbb{E}$ 表示期望值。

举例子

使用总体数据 $2, 4, 6, 8, 10$ 来计算总体方差和样本方差。

总体方差

计算总体平均值：
$\mu = \frac{2 + 4 + 6 + 8 + 10}{5} = 6$
计算每个数据点的平方偏差：
$2 - 6)^2 = 16$
$4 - 6)^2 = 4$
$6 - 6)^2 = 0$
$8 - 6)^2 = 4$
$10 - 6)^2 = 16$
计算总体方差：
$\sigma^2 = \frac{1}{5} (16 + 4 + 0 + 4 + 16) = \frac{40}{5} = 8$

样本方差的无偏估计

假设我们抽取多个样本，每个样本包含3个数据点：

样本 1： $2, 4, 6$

样本平均值：
$\bar{x}_1 = \frac{2 + 4 + 6}{3} = 4$
平方偏差：
$2 - 4)^2 = 4$
$4 - 4)^2 = 0$
$6 - 4)^2 = 4$
样本方差（无偏估计）：
$s^2_1 = \frac{1}{3-1} (4 + 0 + 4) = \frac{8}{2} = 4$
样本 2： $4, 6, 8$
样本平均值：
$\bar{x}_2 = \frac{4 + 6 + 8}{3} = 6$
平方偏差：
$4 - 6)^2 = 4$
$6 - 6)^2 = 0$
$8 - 6)^2 = 4$
样本方差（无偏估计）：
$s^2_2 = \frac{1}{3-1} (4 + 0 + 4) = \frac{8}{2} = 4$
样本 3： $6, 8, 10$
样本平均值：
$\bar{x}_3 = \frac{6 + 8 + 10}{3} = 8$
平方偏差：
$6 - 8)^2 = 4$
$8 - 8)^2 = 0$
$10 - 8)^2 = 4$
样本方差（无偏估计）：
$s^2_3 = \frac{1}{3-1} (4 + 0 + 4) = \frac{8}{2} = 4$
我们看到，不同的样本有不同的方差，但这些样本方差的平均值趋向于总体方差。这是无偏估计的意义：期望值（平均值）等于总体方差。

结论
10. 总体方差：总体所有数据点的平均平方偏差。在例子中，计算得到总体方差为 8。
11. 样本方差（无偏估计）：为了估计总体方差，样本方差用 $n - 1$ 作为分母，使其期望值等于总体方差。对于样本方差来说，使用 $n - 1$ 作为分母确保其期望值等于总体方差。这并不意味着每一个具体的样本方差都等于总体方差，而是多个样本方差的平均值会接近于总体方差。
12. 无偏估计的意义：单个样本方差不一定等于总体方差，但多个样本方差的平均值会接近于总体方差，从而实现无偏估计的目标。无偏估计的概念是基于期望值的。当我们从总体中抽取一个样本并计算样本方差时，我们使用 $n - 1$ 作为分母而不是 $n$ 。这是因为样本均值 $\bar{x}$ 是用所有 $n$ 个数据点计算出来的，这使得样本中的偏差和为零，消耗了一个自由度。使用 $n - 1$ 可以使样本方差成为总体方差的无偏估计。