代码随想录-Day31

455. 分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
在这里插入图片描述

class Solution {// 思路：优先考虑胃口，先喂饱大胃口public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count = 0;int start = s.length - 1;// 遍历胃口for (int index = g.length - 1; index >= 0; index--) {if(start >= 0 && g[index] <= s[start]) {start--;count++;}}return count;}
}

这段代码定义了一个名为Solution的类，并实现了一个方法findContentChildren，该方法意在解决分配饼干的问题。给定两个整数数组g和s，其中g[i]代表第i个孩子的胃口大小，s[j]代表第j块饼干的大小。如果一块饼干可以满足一个孩子的胃口，那么这个孩子就满意了。函数的目标是尽可能让更多的孩子满意，返回最多能满足多少个孩子的胃口。

方法逻辑

预处理：首先，对孩子们的胃口数组g和饼干大小数组s分别进行升序排序。这样可以确保我们总是尝试用最大的饼干去满足最大的胃口，或者用最小的饼干去尝试满足最小的胃口，从而优化分配过程。
分配策略：由于数组已经排序，我们采取从大到小的策略来检查每个孩子的胃口。初始化一个指针start指向饼干数组的最后一个元素（即最大饼干）。对于每个孩子（从胃口最大的开始遍历），我们检查当前最大饼干s[start]是否能满足这个孩子的胃口g[index]。
计数与移动指针：如果当前孩子的胃口不大于（即小于等于）当前可分配的最大饼干，说明这个孩子可以得到满足，计数器count加1，并将饼干指针start向前移动一位，表示这块饼干已经被分配出去了。如果不能满足，则继续检查下一个孩子的胃口。
返回结果：当所有孩子的胃口都被检查过后，返回计数器count的值，即为最多能满足的孩子数量。

这种方法通过排序和从大到小匹配的策略，有效地利用了资源，保证了在饼干有限的情况下满足尽可能多的孩子。

376. 摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个摆动序列，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为摆动序列的最长子序列的长度。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2：

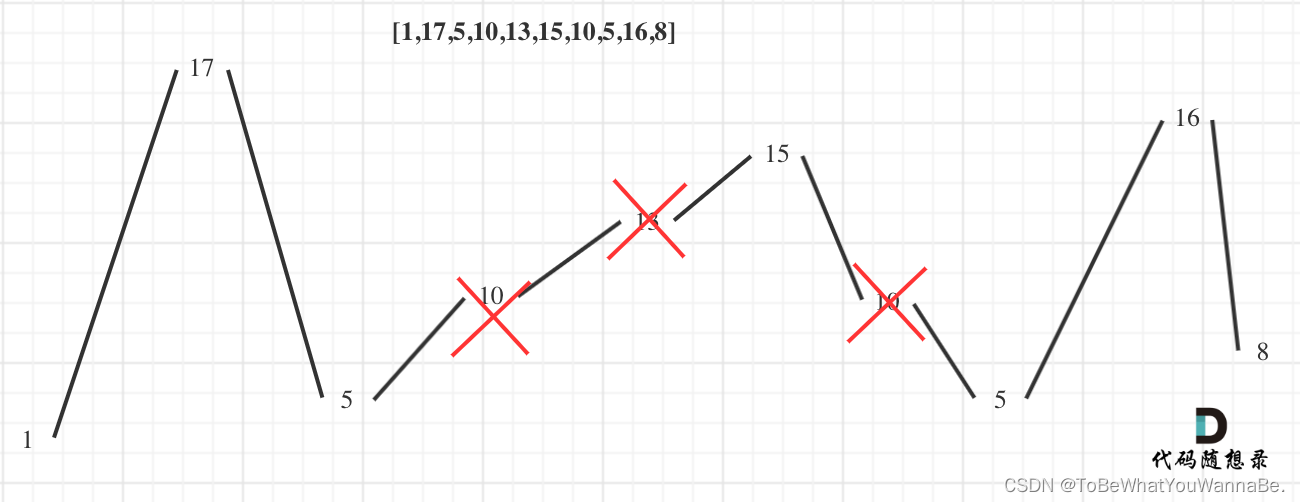
输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2
在这里插入图片描述

class Solution {public int wiggleMaxLength(int[] nums) {if (nums.length <= 1) {return nums.length;}//当前差值int curDiff = 0;//上一个差值int preDiff = 0;int count = 1;for (int i = 1; i < nums.length; i++) {//得到当前差值curDiff = nums[i] - nums[i - 1];//如果当前差值和上一个差值为一正一负//等于0的情况表示初始时的preDiffif ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {count++;preDiff = curDiff;}}return count;}
}

这段代码定义了一个名为Solution的类，其中包含一个方法wiggleMaxLength，用于计算给定整数数组nums中最长的摆动子序列的长度。摆动子序列指的是数组中元素之间的差值在正负之间交替变化的子序列，例如，[1, 7, 4, 9, 2, 5]的最长摆动子序列是[1, 7, 4, 9, 2]或[1, 7, 4, 2, 5]，长度为5。

方法逻辑

边界条件处理：如果输入数组nums的长度小于或等于1，直接返回其长度，因为单个元素或空数组自身即是最长摆动子序列。
初始化变量：定义curDiff表示当前相邻两个元素的差值，preDiff表示上一对相邻元素的差值（初始化时不重要，可以设为0），count用于记录摆动子序列的长度（至少为1，因为单个元素也可视作摆动子序列）。
遍历数组：从第二个元素开始遍历数组，计算当前元素与前一个元素的差值curDiff。
- 如果curDiff与preDiff的符号相反（一正一负，包括preDiff为0的情况，表示首次设置差值），说明满足摆动序列的要求，因此count加1，并更新preDiff为当前差值。
- 否则，继续遍历，因为当前相邻元素差值与前一对差值同号，不足以形成摆动序列的一部分。
返回结果：遍历完成后，count的值即为最长摆动子序列的长度，返回count。

效率分析

此方法的时间复杂度为O(n)，其中n为数组nums的长度，因为它只遍历了数组一次。空间复杂度为O(1)，只使用了常数个额外变量，与输入数组的大小无关。这是一种高效的解法，适合处理大数据量的摆动序列问题。

53. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组
是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

class Solution {public int maxSubArray(int[] nums) {if (nums.length == 1){return nums[0];}int sum = Integer.MIN_VALUE;int count = 0;for (int i = 0; i < nums.length; i++){count += nums[i];sum = Math.max(sum, count); // 取区间累计的最大值（相当于不断确定最大子序终止位置）if (count <= 0){count = 0; // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和}}return sum;}
}

这段代码定义了一个名为Solution的类，其中包含一个方法maxSubArray，用于求解给定整数数组nums中的最大子数组和。这是一个经典问题，也被称为“Kadane算法”。

算法逻辑解释

初始化：首先检查数组长度，如果只有一个元素，直接返回该元素值，因为单个元素本身即为最大子数组和。
变量定义：
- sum 初始化为 Integer.MIN_VALUE，用于记录目前为止找到的最大子数组和。
- count 初始化为0，用于累加当前子数组的和。
遍历数组：遍历输入数组nums的每个元素。
- 对于每个元素，将其值累加到count上，表示当前子数组的和。
- 使用Math.max(sum, count)更新sum，确保它始终保存到目前为止观察到的最大子数组和。
- 如果count（当前子数组的和）小于等于0，这意味着继续向当前子数组添加元素不会增加总和（因为非负数加负数会使和变小，非正数加正数至多不变），因此重置count为0，相当于开始考虑以下一个元素作为新子数组的起点。
返回结果：遍历结束后，sum即为最大子数组之和，返回sum。