一些激活函数
- 摘要
- 激活函数分类
- sigmoid
- Tanh
- Softsign
- Softmax
- ReLU
- Softplus
- Noisy ReLU
- Leaky ReLU
- PRelu
- ELU
- SELU
- Swish
- GELU
- GLU
- GEGLU
- Mish
- Maxout
摘要
本篇博客对一些激活函数进行总结,以便加深理解和记忆
激活函数分类
-
饱和激活函数:sigmoid、tanh…
-
非饱和激活函数:ReLU、LeakyRelu、ELU、PReLU、RReLU…
-
饱和的概念:设激活函数f(x),当x趋近于正负无穷时,f(x)趋近于0
-
非饱和激活函数的优点
- 非饱和激活函数能解决深层网络带来的梯度消失问题
- 非饱和激活函数有助于加快收敛速度
- 非饱和激活函数能解决深层网络带来的梯度消失问题
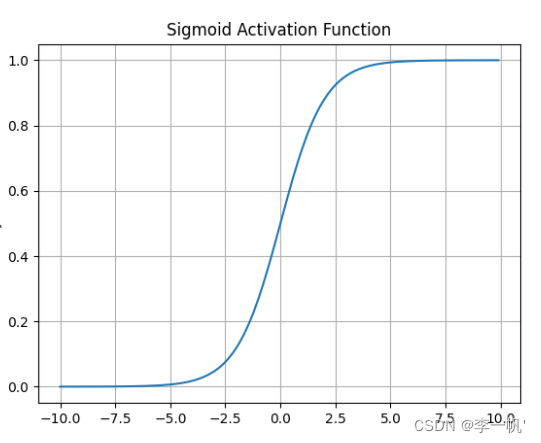
sigmoid
- 公式: f ( x ) = 1 1 + e − x f(x)= \frac 1 {1+e^{-x}} f(x)=1+e−x1
- 导数公式: f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x))
- 何时使用
- 将模型的值压缩到[0,1]范围内的概率值,适用于二分类或置信度
- 梯度平滑,便于求导
- 缺点
- 容易造成梯度消失。我们从导函数图像中了解到sigmoid的导数都是小于0.25的,那么在进行反向传播的时候,梯度相乘结果会慢慢的趋向于0。这样几乎就没有梯度信号通过神经元传递到前面层的梯度更新中,因此这时前面层的权值几乎没有更新,这就叫梯度消失。除此之外,为了防止饱和,必须对于权重矩阵的初始化特别留意。如果初始化权重过大,可能很多神经元得到一个比较小的梯度,致使神经元不能很好的更新权重提前饱和,神经网络就几乎不学习
- 函数输出不是以 0 为中心的,梯度可能就会向特定方向移动,从而降低权重更新的效率
- 执行指数运算,计算机运行得较慢,比较消耗计算资源
Sigmoid函数在历史上曾非常常用,但是现在它已经不太受欢迎,实际中很少使用
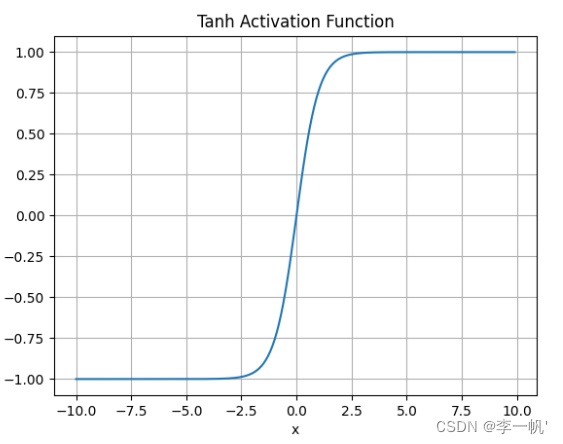
Tanh
- 公式: f ( x ) = e x − e − x e x + e − x ( = 2 s i g m o i d ( 2 x ) − 1 ) f(x) = \frac {e^x - e^{-x}} {e^x + e^{-x}} \;\;\;(=2sigmoid(2x)-1) f(x)=ex+e−xex−e−x(=2sigmoid(2x)−1)
- 何时使用
- 映射范围为[-1,1],且函数以0为中心,比sigmoid更好
- 负输入将被强映射为负,而零输入被映射为接近零
- 缺点
- 仍然存在梯度饱和的问题
- 依然进行的是指数运算
Softsign
- 公式: f ( x ) = x 1 + ∣ x ∣ f(x) = \frac x {1+|x|} f(x)=1+∣x∣x
- 导数: f ′ ( x ) = 1 ( 1 + ∣ x ∣ ) 2 f'(x)= \frac 1 {(1+|x|)^2} f′(x)=(1+∣x∣)21
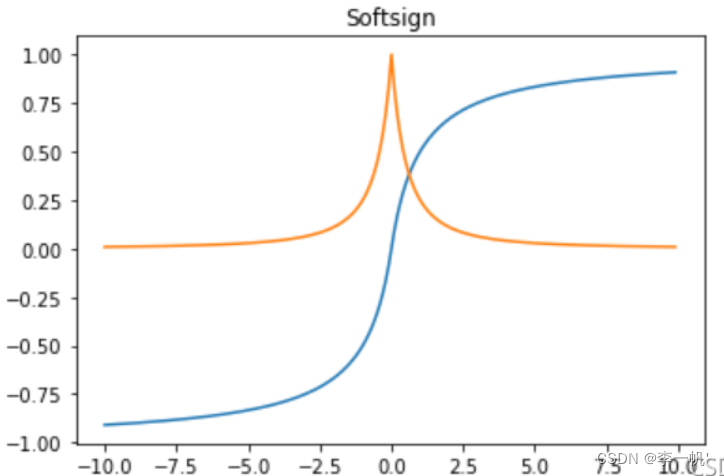
- Softsign函数是Tanh函数的另一个替代选择,是反对称、去中心、可微分,并返回-1和1之间的值。其更平坦的曲线与更慢的下降导数表明它可以更高效地学习,比tTanh函数更好的解决梯度消失的问题
- Softsign函数的导数的计算比Tanh函数更复杂
Softmax
- 公式: f ( x ) = e X i ∑ i e X i f(x)= \frac {e^{X_i}} {\sum_i e^{X_i}} f(x)=∑ieXieXi
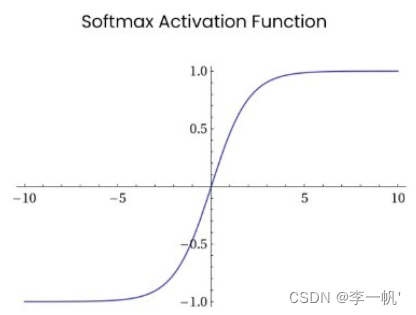
Softmax函数常在神经网络输出层充当激活函数,将输出层的值通过激活函数映射到0-1区间,将神经元输出构造成概率分布,用于多分类问题中
ReLU
- 公式: f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
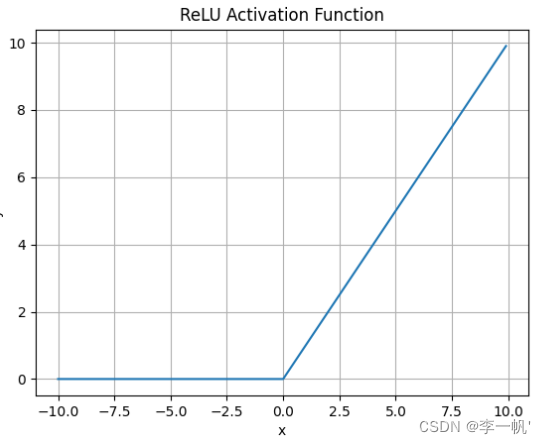
- 何时使用
- ReLU解决了梯度消失的问题,当输入值为正时,神经元不会饱和
- 由于ReLU线性、非饱和的性质,在SGD中能够快速收敛
- 计算复杂度低,不需要进行指数运算
- 缺点
- 输出不是以0为中心的
- Dead ReLU 问题。当输入为负时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新
训练神经网络的时候,一旦学习率没有设置好,第一次更新权重的时候,输入是负值,那么这个含有ReLU的神经节点就会死亡,再也不会被激活。所以,要设置一个合适的较小的学习率,来降低这种情况的发生
Softplus
- 公式: f ( x ) = l o g ( 1 + e x ) f(x)=log(1+e^x) f(x)=log(1+ex)
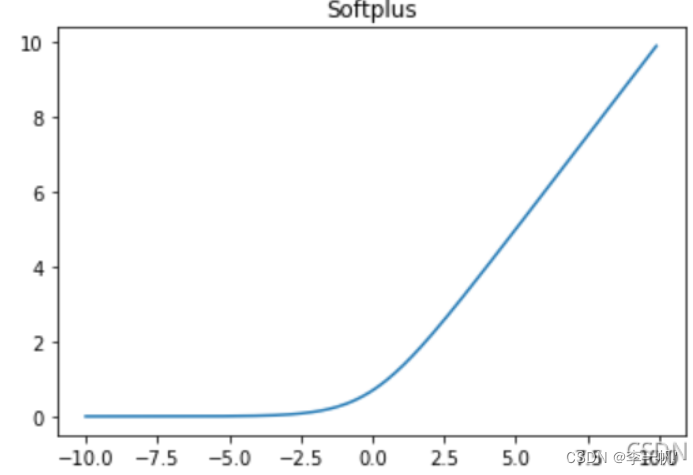
Softplus函数可以看作是ReLU函数的平滑
Noisy ReLU
- 公式: f ( x ) = m a x ( 0 , x + Y ) , Y N ( 0 , σ ( x ) ) f(x)=max(0,x+Y),Y~N(0,σ(x)) f(x)=max(0,x+Y),Y N(0,σ(x))
ReLU被扩展以包括高斯噪声(Gaussian noise),在受限玻尔兹曼机解决计算机视觉任务中得到应用,实验结果表明Maxout与Dropout组合使用可以发挥比较好的效果
Leaky ReLU
- 公式: f ( x ) = m a x ( a x , x ) f(x)=max(ax,x) f(x)=max(ax,x)
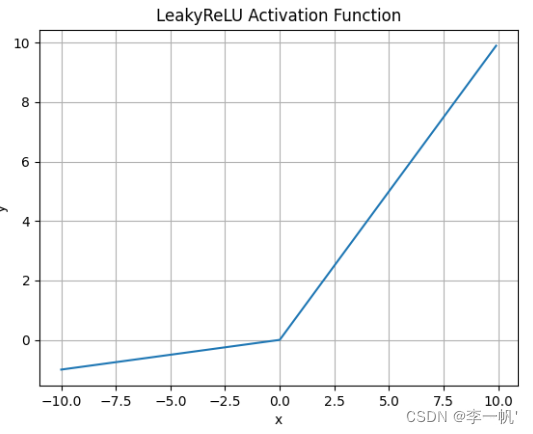
- 何时使用
- 解决了ReLU输入值为负时神经元出现的死亡的问题
- Leaky ReLU线性、非饱和的性质,在SGD中能够快速收敛
- 计算复杂度低,不需要进行指数运算
- 缺点
- 函数中的α,需要通过先验知识人工赋值(一般设为0.01)
- 有些近似线性,导致在复杂分类中效果不好
从理论上讲,Leaky ReLU 具有 ReLU 的所有优点,而且 Dead ReLU 不会有任何问题,但在实际操作中,尚未完全证明 Leaky ReLU 总是比 ReLU 更好
PRelu
- 公式
f ( a , x ) = [ a x , x < 0 x , x ≥ 0 ] f(a,x) = \begin{bmatrix} ax,\;\;\;x<0\\x,x≥0 \end{bmatrix} f(a,x)=[ax,x<0x,x≥0]

PRelu激活函数也是用来解决ReLU带来的神经元坏死的问题。与Leaky ReLU激活函数不同的是,PRelu激活函数负半轴的斜率参数α 是通过学习得到的,而不是手动设置的恒定值
ELU
- 公式
f ( a , x ) = [ a ( e x − 1 ) , x ≤ 0 x , x > 0 ] f(a,x)=\begin{bmatrix} a(e^x-1),\;\;x≤0\\x,x>0 \end{bmatrix} f(a,x)=[a(ex−1),x≤0x,x>0]

- 何时使用
- ELU试图将激活函数的输出均值接近于零,使正常梯度更接近于单位自然梯度,从而加快学习速度
- ELU 在较小的输入下会饱和至负值,从而减少前向传播的变异和信息
- 缺点
- 计算的时需要计算指数,计算效率低
与Leaky ReLU和PRelu激活函数不同的是,ELU激活函数的负半轴是一个指数函数而不是一条直线
SELU
- 公式
f ( a , x ) = λ [ a ( e x − 1 ) , x ≤ 0 x , x > 0 ] , λ = 1.0507 , a = 1.6733 f(a,x)=λ \begin{bmatrix} a(e^x-1),\;\;x≤0\\x,x>0 \end{bmatrix},\;\;λ=1.0507,a=1.6733 f(a,x)=λ[a(ex−1),x≤0x,x>0],λ=1.0507,a=1.6733
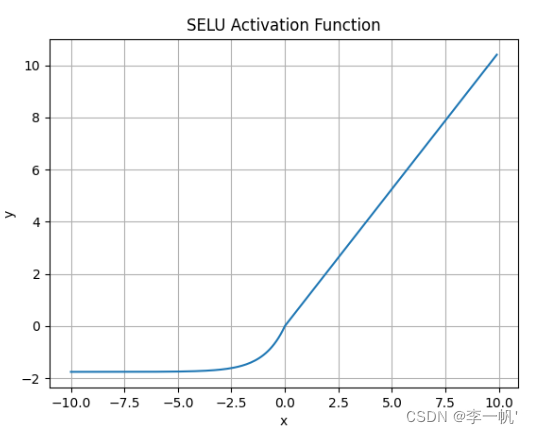
- SELU 允许构建一个映射 g,其性质能够实现 SNN(自归一化神经网络)
- SNN 不能通过ReLU、sigmoid 、tanh 和 Leaky ReLU 实现
- 这个激活函数需要有:
- 负值和正值,以便控制均值
- 饱和区域(导数趋近于零),以便抑制更低层中较大的方差
- 大于 1 的斜率,以便在更低层中的方差过小时增大方差
- 连续曲线。后者能确保一个固定点,其中方差抑制可通过方差增大来获得均衡。通过乘上指数线性单元(ELU)来满足激活函数的这些性质,而且 λ>1 能够确保正值净输入的斜率大于 1
SELU激活函数是在自归一化网络中定义的,通过调整均值和方差来实现内部的归一化,这种内部归一化比外部归一化更快,这使得网络能够更快得收敛
Swish
- 公式: f ( x ) = x ∗ s i g m o i d ( x ) f(x)=x*sigmoid(x) f(x)=x∗sigmoid(x)
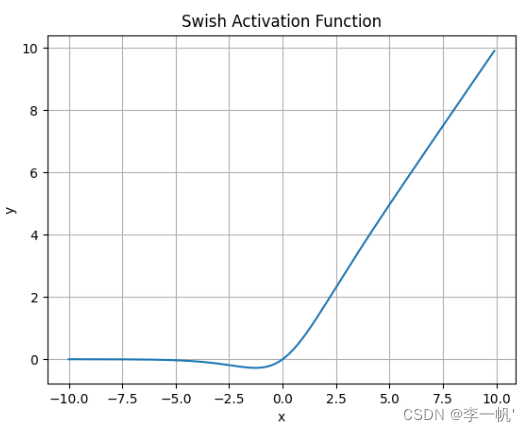
- Swish激活函数无界性有助于防止慢速训练期间,梯度逐渐接近 0 并导致饱和
- 有界性也是有优势的,因为有界激活函数可以具有很强的正则化(防止过拟合, 进而增强泛化能力),并且较大的负输入问题也能解决
- Swish激活函数在x=0附近更为平滑,而非单调的特性增强了输入数据和要学习的权重的表达能力
GELU
- 公式
f ( x ) = x ∗ p = x Φ ( x ) , Φ 为标准正态分布的积累分布函数 Φ ( x ) = 1 2 Π ∫ − ∞ x e − t 2 2 d t = 1 2 ( 1 + e r f ( x 2 ) ) e r f ( x ) = 1 Π ∫ − x x e − t 2 d t = 2 Π ∫ 0 x e − t 2 d t ,高斯误差函数 , 与 t a n h ( x ) 比较接近 f(x)=x*p=xΦ(x),\;\;Φ为标准正态分布的积累分布函数\\ Φ(x)=\frac 1 {\sqrt{2Π}} \int_{-∞}^xe^{-\frac {t^2} 2} dt = \frac 1 2(1+erf(\frac x {\sqrt 2}))\\ erf(x)=\frac 1 {\sqrt Π}\int_{-x}^xe^{-t^2}dt=\frac 2{\sqrt Π}\int_0^xe^{-t^2}dt,高斯误差函数,与 tanh(x) 比较接近 f(x)=x∗p=xΦ(x),Φ为标准正态分布的积累分布函数Φ(x)=2Π1∫−∞xe−2t2dt=21(1+erf(2x))erf(x)=Π1∫−xxe−t2dt=Π2∫0xe−t2dt,高斯误差函数,与tanh(x)比较接近 - GELU(高斯误差线性单元)是一个非初等函数形式的激活函数,是RELU的变种,被GPT-2、BERT、RoBERTa、ALBERT 等NLP模型所采用,将ReLU及其变种与Dropout合二为一
- GELU 与 Swish 激活函数的函数形式和性质非常相像,一个是固定系数 1.702,另一个是可变系数 β(可以是可训练的参数,也可以是通过搜索来确定的常数),两者的实际应用表现也相差不大
GLU
- 公式
G L U ( a , b ) = a ⊙ s i g m o i d ( b ) G L U ( x , W , V ) = s i g m o i d ( x W ) ⊙ x V GLU(a,b)=a⊙sigmoid(b)\\ GLU(x,W,V)=sigmoid(xW)⊙xV GLU(a,b)=a⊙sigmoid(b)GLU(x,W,V)=sigmoid(xW)⊙xV - GLU通过门控机制对输出进行把控,像Attention一样可看作是对重要特征的选择。其优势是不仅具有通用激活函数的非线性,而且反向传播梯度时具有线性通道,类似ResNet残差网络中的加和操作传递梯度,能够缓解梯度消失问题
- 由于 sigmoid和tanh的导数会downscaling,导致梯度消失问题。而GLU相比sigmoid多出一个线性乘积项,因此能够加速收敛
GEGLU
- 公式
G E G L U ( x , W , V ) = G E L U ( x W ) ⊙ x V GEGLU(x,W,V)=GELU(xW)⊙xV GEGLU(x,W,V)=GELU(xW)⊙xV - GEGLU是GLU激活函数的变体,将GLU中的sigmoid替换为GELU,Google的T5 Transformer模型中对Feed-Forward Network采用了GEGLU,性能提升比较显著
- 除了用GELU替代GLU中的sigmoid外,还可用ReLU、Swish等,甚至取消其中的激活函数(Bilinear(x, W, V) = xW · xV),但是这些变体相比GLU差异不是特别显著
Mish
- 公式: f ( x ) = x ∗ t a n h ( l n ( 1 + e x ) ) f(x)=x*tanh(ln(1+e^x)) f(x)=x∗tanh(ln(1+ex))
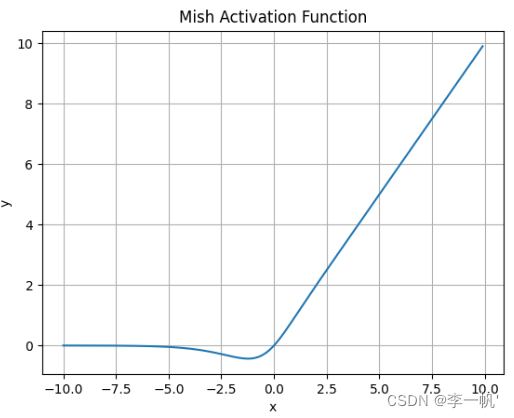
Mish激活函数的函数图像与Swish激活函数类似,但要更为平滑一些,缺点是计算复杂度要更高一些
Maxout
- 公式: h i ( x ) = m a x j ∈ [ 1 , k ] z i j , z i j = x T W i j + b i j , W ∈ R d ∗ m ∗ k h_i(x)=max_{j∈[1,k]}z_{ij},z_{ij}=x^TW_{ij}+b_{ij},W∈R^{d*m*k} hi(x)=maxj∈[1,k]zij,zij=xTWij+bij,W∈Rd∗m∗k
- 优点
- 拟合能力非常强,可以拟合任意的凸函数
- 具有ReLU的所有优点,线性、不饱和性
- 没有ReLU的一些缺点,如:神经元的死亡
- 缺点:每个神经元中有两组(w,b)参数,那么参数量就增加了一倍,导致了整体参数的数量激增
Maxout可以看做是在深度学习网络中加入一层激活函数层,包含一个参数k.这一层相比ReLU,sigmoid等,其特殊之处在于增加了k个神经元,然后输出激活值最大的值