目录
- 引言
- 名词替代
- 影响模型偏差和方差的因素
- 1.多项式阶数
- 2.正则化参数
- 判断是否有高偏差或高方差
- 1.方法一:建立性能基准水平
- 2.方法二:建立学习曲线
- 解决线性回归高偏差或高方差
- 解决神经网络的高偏差或高方差
- 1.回顾机器学习问题
- 2.神经网络高方差和高偏差
- 3.神经网络正则化
- 神经网络如何正则化
- 总结
引言
机器学习系统开发的典型流程是从一个想法开始,然后训练模型。初次训练的结果通常不理想,因此关键在于如何决定下一步该做什么以提高模型性能。观察算法的偏差和方差(Bias and Variance)在很多应用场景中能很好地指导下一步的改进。
名词替代
J_train:训练误差
J_cv:交叉验证误差
J_test:测试误差
影响模型偏差和方差的因素
1.多项式阶数
(1)什么是高偏差和高方差
- 如果用一条直线来拟合数据,效果不好,则认为此时模型有高偏差,高偏差的模型J_train和J_cv都很高,表现为欠拟合。
- 如果用一个四阶多项式来拟合数据,则认为此时模型有高方差,高方差的模型J_train很低,但J_cv很高,表现为过拟合。
- 如果用一个二次多项式来拟合数据,效果最好,此时模型既没有高偏差也没有高方差,合适的模型J_train和J_cv都较低。
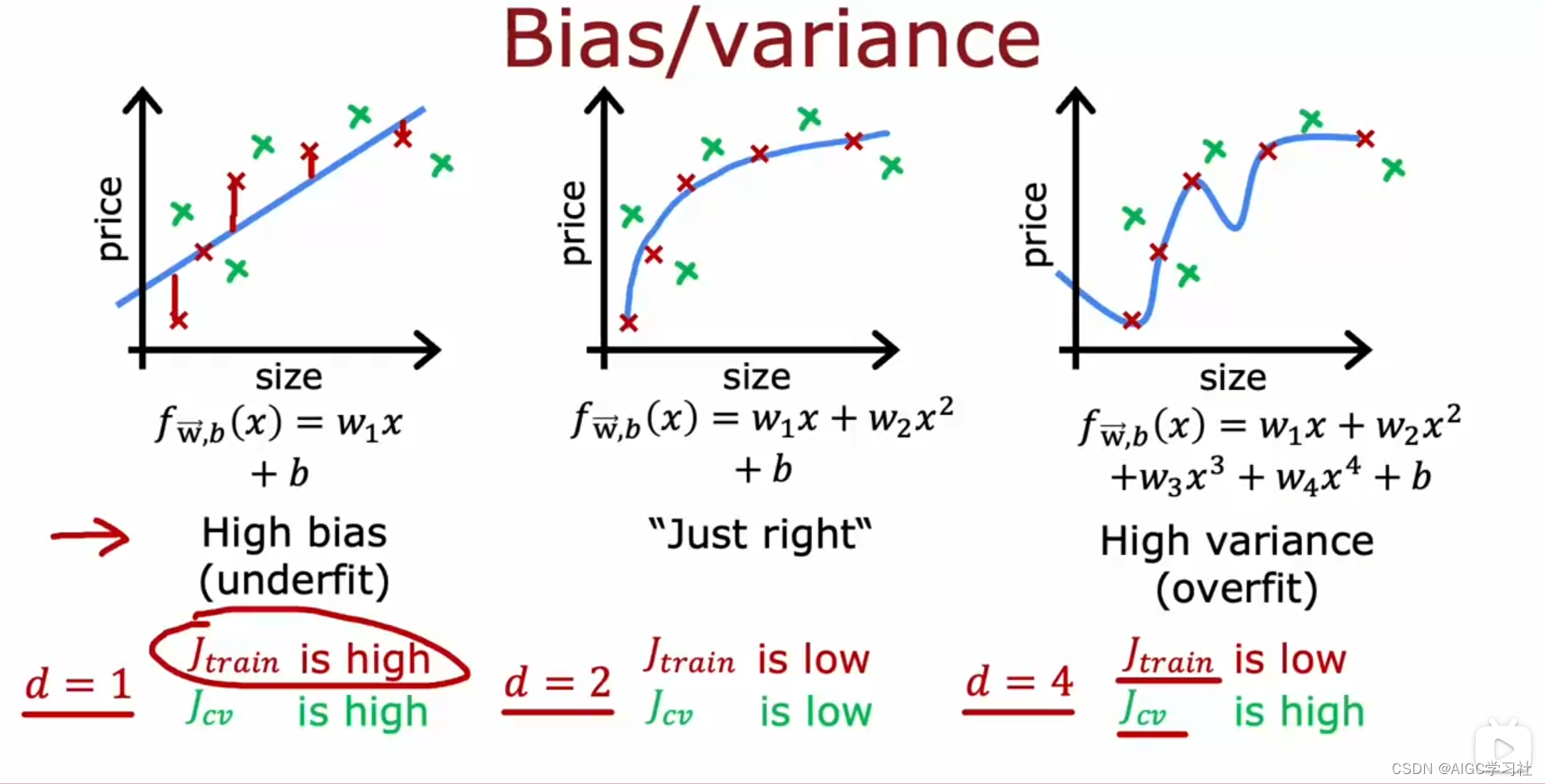
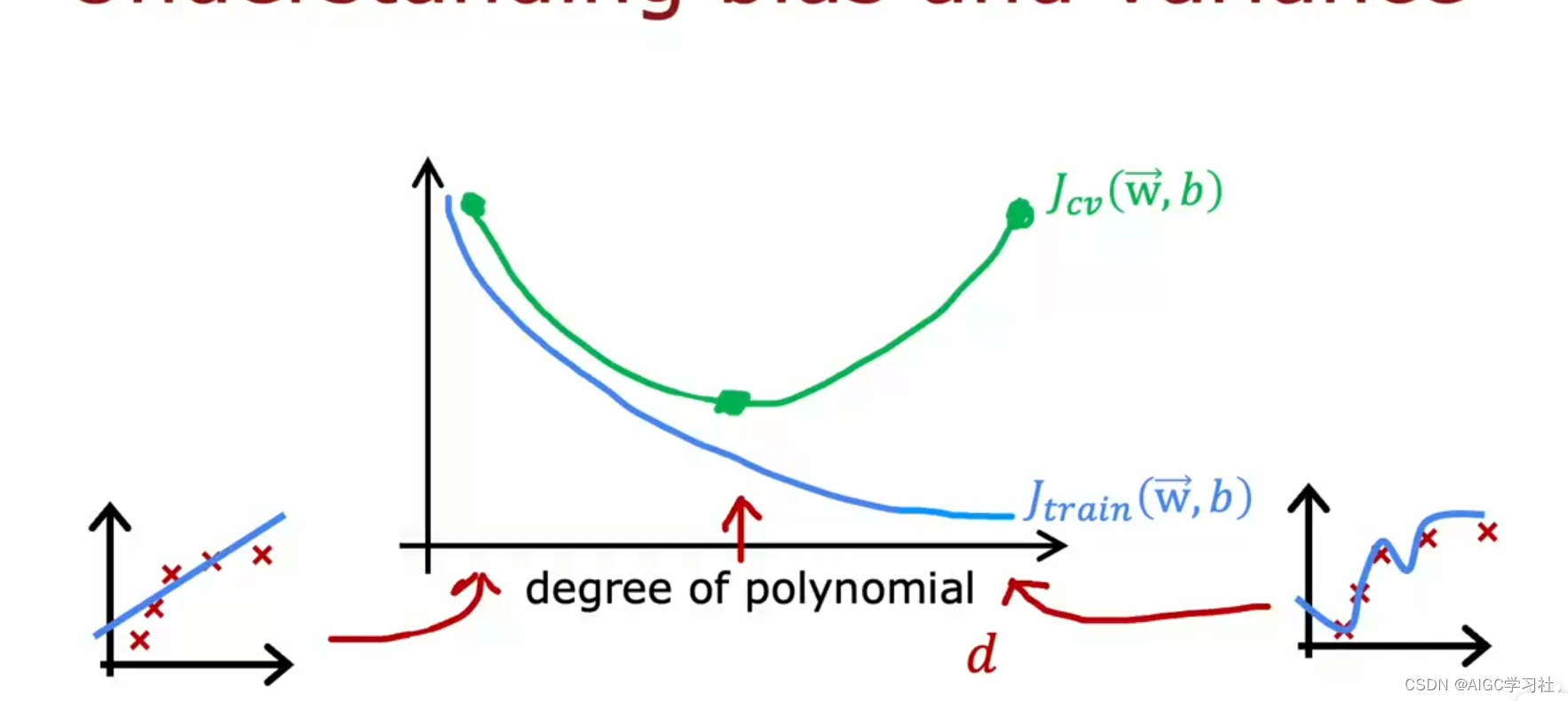
(2) 模型复杂度对模型表现的影响
当多项式阶数(模型复杂度)增加时:
- J_train会下降,因为模型变得更加复杂,更能拟合训练数据,此时模型高偏差。
- J_cv在多项式次数(d)很低时很高,表示欠拟合,此时模型高偏差;在多项式次数(d)很高时也很高,表示过拟合,此时模型高方差。
只有在适中的多项式次数(如二次多项式)时,模型的J_train和J_cv都较低,表现最好。 因此要选择一个合适的多项式次数,使模型在训练数据和未见过的数据上都有较好的表现,达到偏差和方差的平衡。
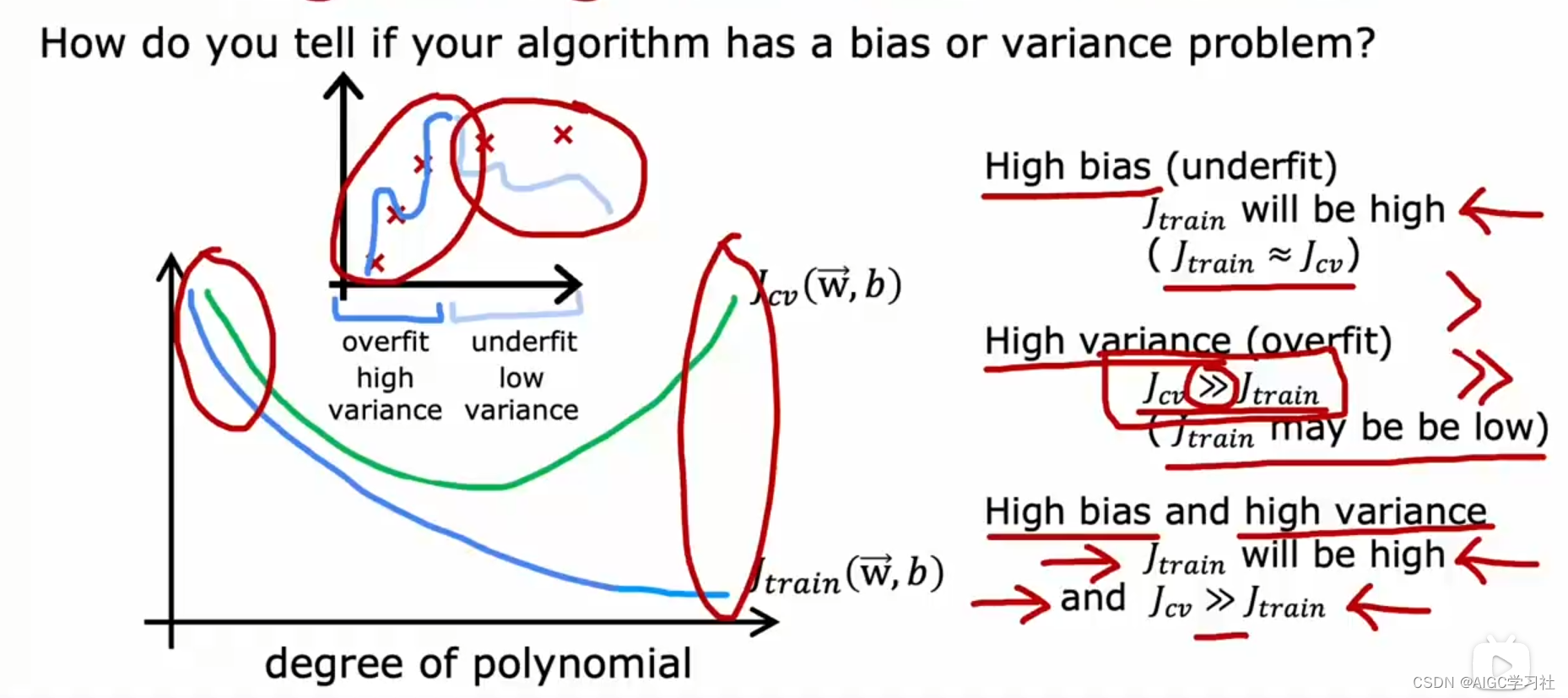
(3)结论
-
高偏差(欠拟合):主要指标是J_train高,表示模型在训练集上表现不好。通常J_train和J_cv接近。
-
高方差(过拟合):主要指标是J_cv远高于J_train,即J_cv >> J_train。训练误差低但交叉验证误差高,表明模型在训练数据上表现好但在新数据上表现差。
-
同时存在高偏差和高方差:这种情况较少见,但在某些复杂模型如神经网络中可能出现。表现为训练误差高,交叉验证误差更高。
-
关键在于:高偏差表示模型在训练集上表现不好,高方差表示模型在交叉验证集上比在训练集上表现差得多。
2.正则化参数
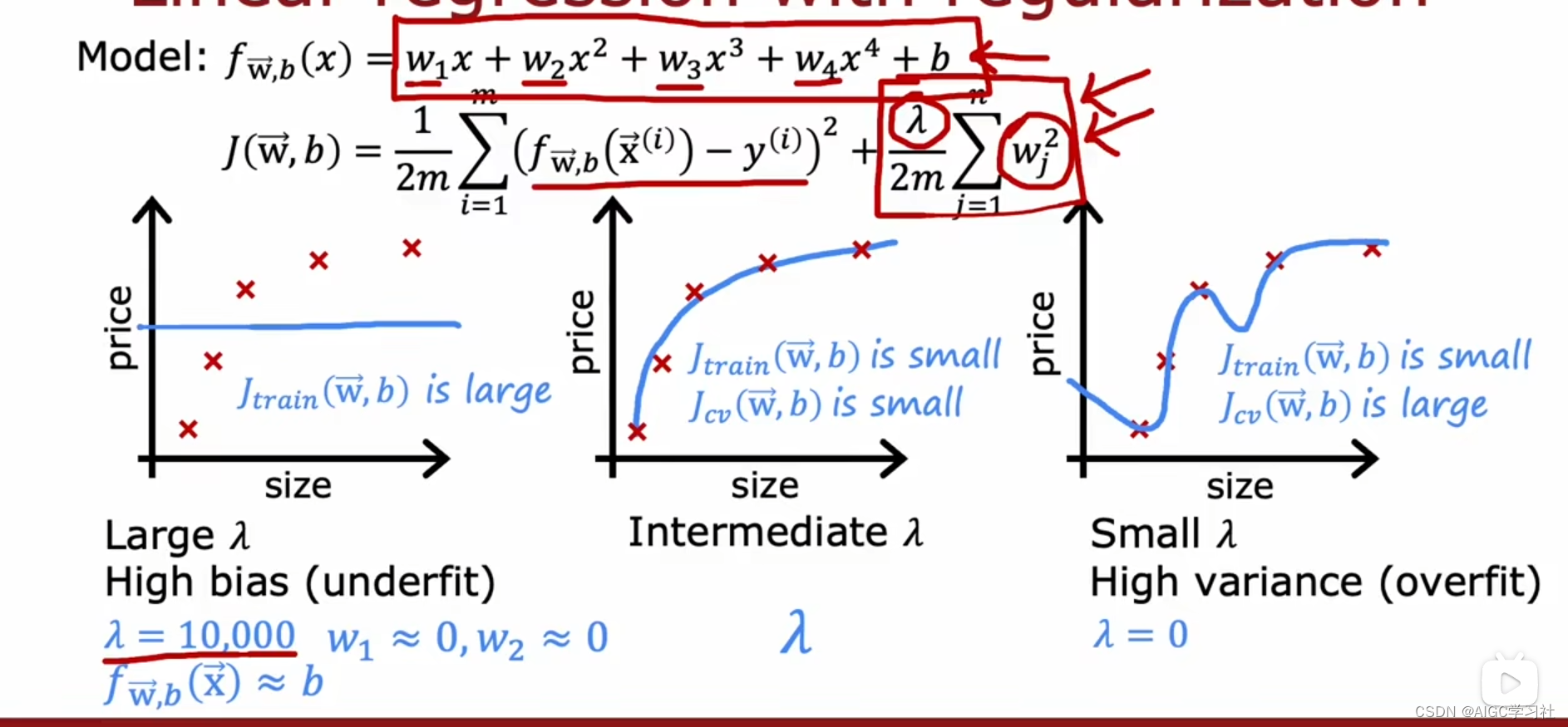
(1)过大的λ和过小的λ
λ过大导致模型高偏差(欠拟合),w参数几乎为0没有影响了,只有λ的常量值,此时模型绘制出来就是一条线,因此无法拟合训练样本,Jtrain较高。λ过小导致模型高方差(过拟合),Jcv远大于Jtrain。最终,合适的λ值能平衡偏差和方差,减少训练集和验证集的误差。
(2)通过交叉验证选择适合的λ
类似于之前选择多项式阶数的方法,先设定λ值(如λ=0),最小化成本函数得到参数,然后计算J_cv。不断尝试不同的λ值,逐步翻倍,并计算每次的J_cv。最终,通过比较不同λ值对应的J_cv差,选择J_cv最小的λ值及其对应的参数。最后,用J_test评估算法的泛化性能,并展示J_train和J_cv如何随λ变化。

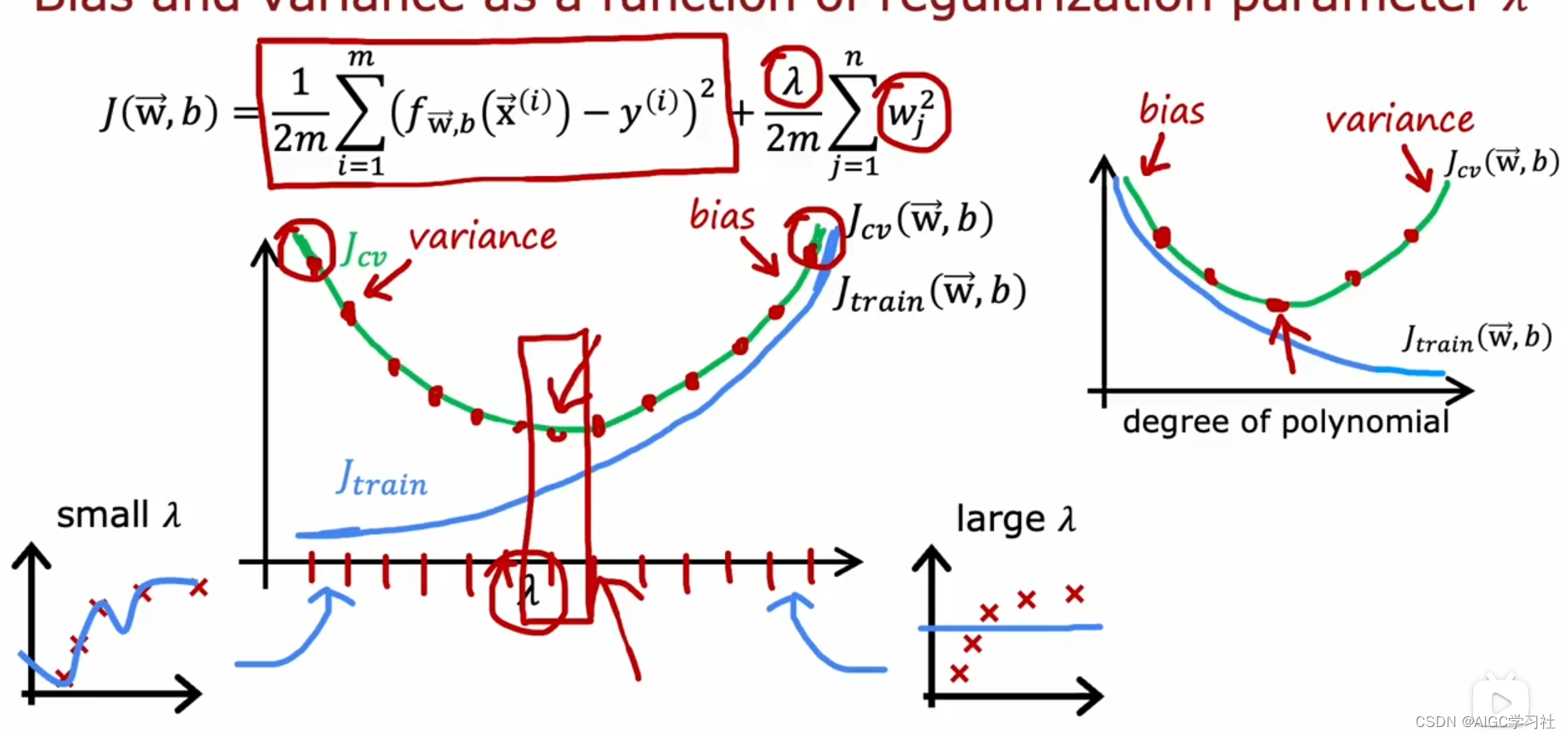
(3)正则化参数λ对模型表现的影响
当正则化参数(λ)变大时:
- λ=0时表示没有正则化,容易过拟合(高方差),J_train小而J_cv大。
- λ值很大时会欠拟合(高偏差),导致J_train和J_cv都很大。随着λ增大,J_train增加。两端λ值过大或过小时J_cv都会增加。
适中的λ值可以使模型性能最佳,J_train和J_cv都较低。 最终得出结论:通过交叉验证尝试不同的λ值,选择J_cv最小的λ值,可以得到合适的模型。类似于选择多项式次数,两者图形在偏差和方差方面是镜像关系。
判断是否有高偏差或高方差
1.方法一:建立性能基准水平
(1)语音识别案例概述
训练一个语音识别系统,J_train(没有正确转录的部分占总体的比例)为10.8%,J_cv(测试系统性能)为14.8%。尽管10.8%看起来像是高偏差,但通过与人类表现(10.6%误差)对比,发现算法在训练集上的表现接近人类水平,仅差0.2%。真正的问题是J_cv比J_train高很多,有4%的差距,这表明算法存在高方差问题,而不是高偏差问题。通过这样的基准测试,可以更准确地判断算法性能的不足之处。

(2)建立性能基准水平的三种方法
在判断训练误差是否高时,建立性能的基准水平很有用。基线水平帮助你对学习算法的误差有合理的预期。
- 常见的方法是衡量人类在该任务上的表现,因为人类通常擅长处理非结构化数据(如音频、图像或文本)。
- 另一种方法是参考已有的竞争算法或之前的实现,通过测量这些算法的性能来建立基准。
- 有时也可以根据之前的经验进行猜测。

(3)性能基准水平判断高偏差和高方差
首先,通过建立性能基准水平(如人类表现)和测量训练误差及交叉验证误差来评估算法的性能。 - (左侧)如果训练误差高于基线水平,则算法存在高偏差。
- (中间)如果交叉验证误差远高于训练误差,则表明算法有高方差。
通过这些数值差距,可以直观地判断算法的问题。(右侧)有时算法可能同时存在高偏差和高方差,具体表现为训练误差高于基线水平,且训练误差与交叉验证误差之间的差距很大。理解这些指标有助于更好地分析和改进算法。

(4)小结
判断算法是否有高偏差的一种方法是看训练误差是否大,然而,在某些应用中,数据可能嘈杂,零误差不现实,因此建立性能基准很有用。你可以将训练误差与期望误差(如人类表现)对比,来判断误差是否大。同样,比较交叉验证误差和训练误差,来判断算法是否有高方差问题。通过这些方法,可以准确评估算法的偏差和方差问题。此外,学习曲线也是理解算法性能的一个有用工具。
2.方法二:建立学习曲线
学习曲线(Learning curves)是一种帮助你了解学习算法性能如何的方式,曲线随着经验的数量发生变化。,经验数量指的是算法所拥有的训练样本数。
(1)训练样本数的变化与J_train,J_cv
学习曲线帮助了解学习算法性能随训练样本数量变化的方式。横轴表示训练样本数,纵轴表示误差,包括训练误差(J_train)和交叉验证误差(J_cv)。当训练样本增多,交叉验证误差减少,因为模型变得更好。而训练误差则会增加,因为随着样本增多,模型很难完美拟合所有训练样本。少量样本时,训练误差接近零,但样本增多后,误差会增加。
通常交叉验证误差比训练误差高,因为模型更好地拟合了训练集。
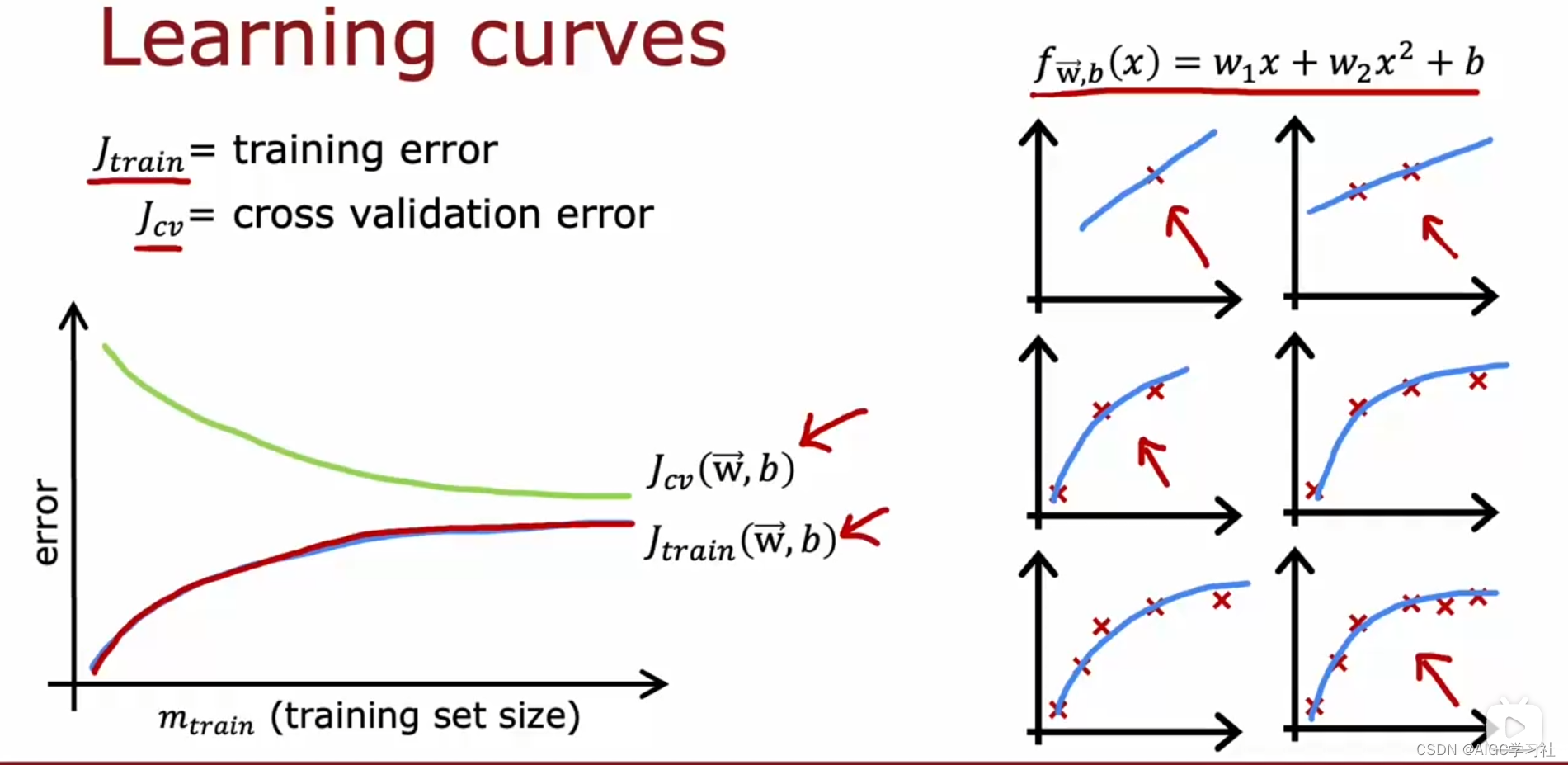
(2)高偏差的学习曲线
高偏差情况下,训练误差和交叉验证误差随着样本增加,初期会下降但随后趋于平稳。这是因为模型太简单(如线性函数),无法适应更多数据,即使增加训练数据,误差也不会降低。
通过比较基准线(如人类表现),可以看到J_train与基准线的较大误差(间隙较大),说明高偏差问题。结论是,如果算法有高偏差,增加更多训练数据效果不大,需要其他方法改善算法性能。
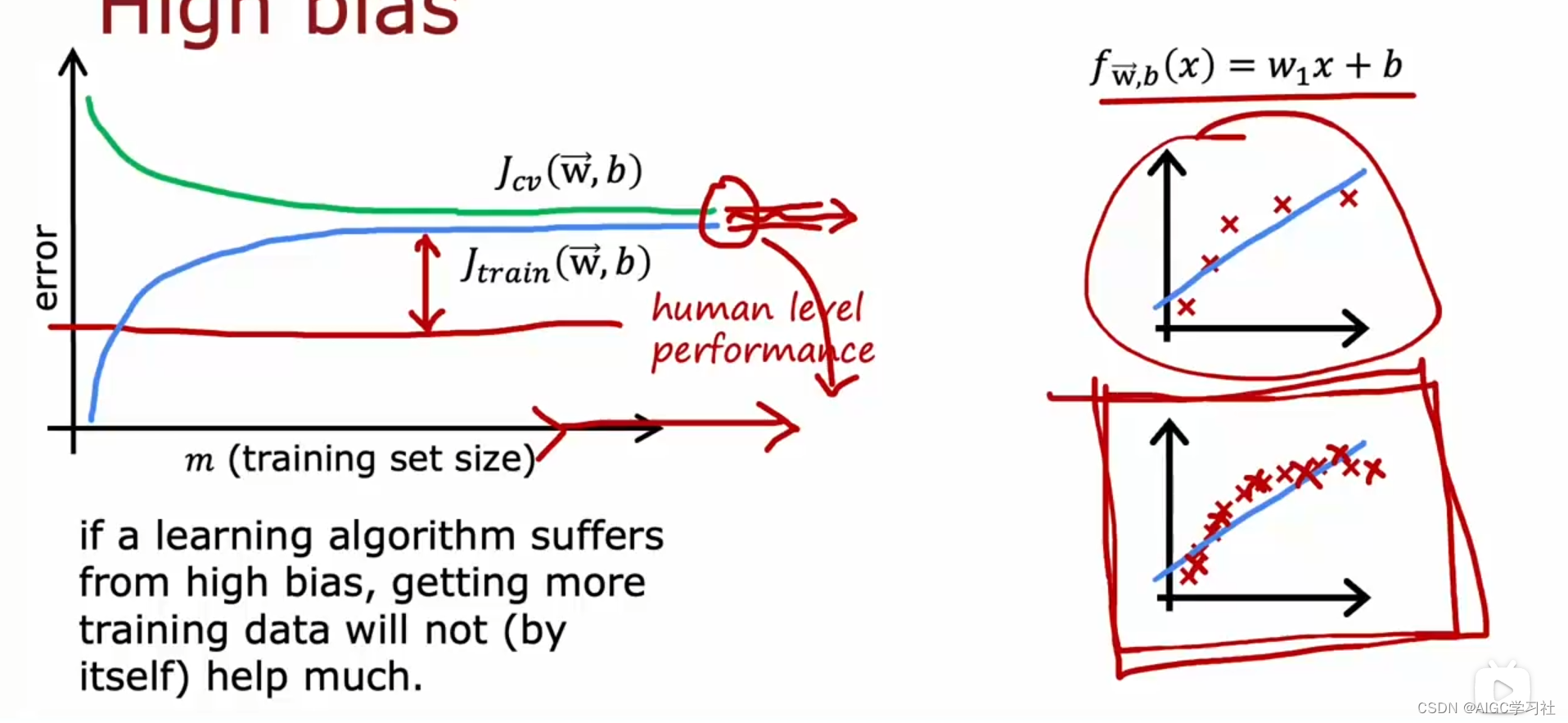
(3)高方差的学习曲线
高方差情况下,训练误差(J_train)随训练集变大而增加,但交叉验证误差(J_cv)更高,两者之间差距大,表明模型在训练集上表现好但不能泛化。高方差的信号是交叉验证误差远高于训练误差。
增加训练数据有助于降低交叉验证误差,使其接近训练误差,从而改善算法性能。因此,扩展训练集对高方差算法有显著帮助,但对高偏差算法效果不大。总结来说,更多的训练数据可以帮助高方差算法降低误差,提高性能。
解决线性回归高偏差或高方差
回到本周最初的例子,如果房价预测算法错误频繁,首先观察训练误差(J_train)和交叉验证误差(J_cv)或绘制学习曲线,来判断算法是高偏差还是高方差,然后根据影响方差和偏差的因素,分别应对高偏差和高方差问题。
-
高偏差(欠拟合)问题:
- 添加更多特征
- 添加多项式特征
- 减小正则化参数(λ)
-
高方差(过拟合)问题:
- 获取更多训练样本
- 使用更小的特征集
- 增加正则化参数(λ)
总结而言,增加数据和简化模型有助于解决高方差,而增强模型能力和灵活性有助于解决高偏差。缩小训练集并不能有效解决高偏差问题,还可能导致交叉验证误差增加和性能下降。
解决神经网络的高偏差或高方差
1.回顾机器学习问题
高偏差和高方差都会损害算法的性能。神经网络结合大数据的理念,能够处理大型数据集,提供了解决高偏差和高方差的新方法。如果对数据集拟合不同阶数的多项式,简单的线性模型会有高偏差,而复杂模型会有高方差,需要在两者之间找到平衡。在神经网络出现之前,机器学习工程师常讨论这种偏差方差权衡,通过调整模型复杂度来平衡偏差和方差。神经网络提供了一种新的方法来解决这种权衡问题,虽然有一些限制。
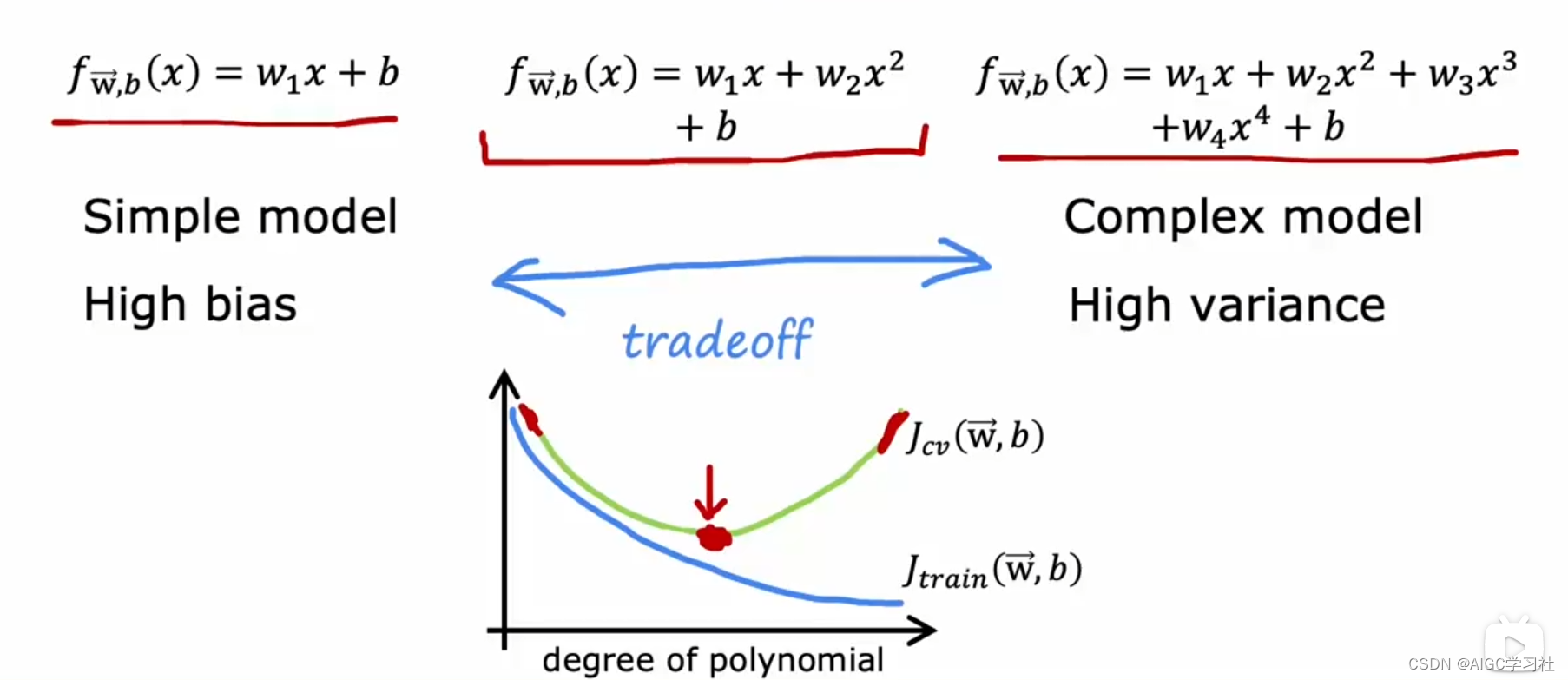
2.神经网络高方差和高偏差
大型神经网络在中小型数据集上训练时,通常是低偏差机器,即能很好地拟合训练集,从而为减少偏差和方差提供了新方法。具体步骤包括:
- 在训练集上训练神经网络,测量训练误差J_train。如果误差高,表明有高偏差问题,可以增大神经网络的规模(增加隐藏层或单元数)。
- 如果在训练集上表现良好,检查交叉验证误差J_cv。如果交叉验证误差高于训练误差,表明有高方差问题,可以通过增加数据来解决。
- 重复上述步骤,直到模型在交叉验证集上表现良好。
该方法的限制包括计算成本高和数据有限,但在能获取大量数据的情况下,这种方法在许多应用中表现良好。在开发过程中,根据当前高偏差或高方差的情况,采取相应措施以优化算法性能。
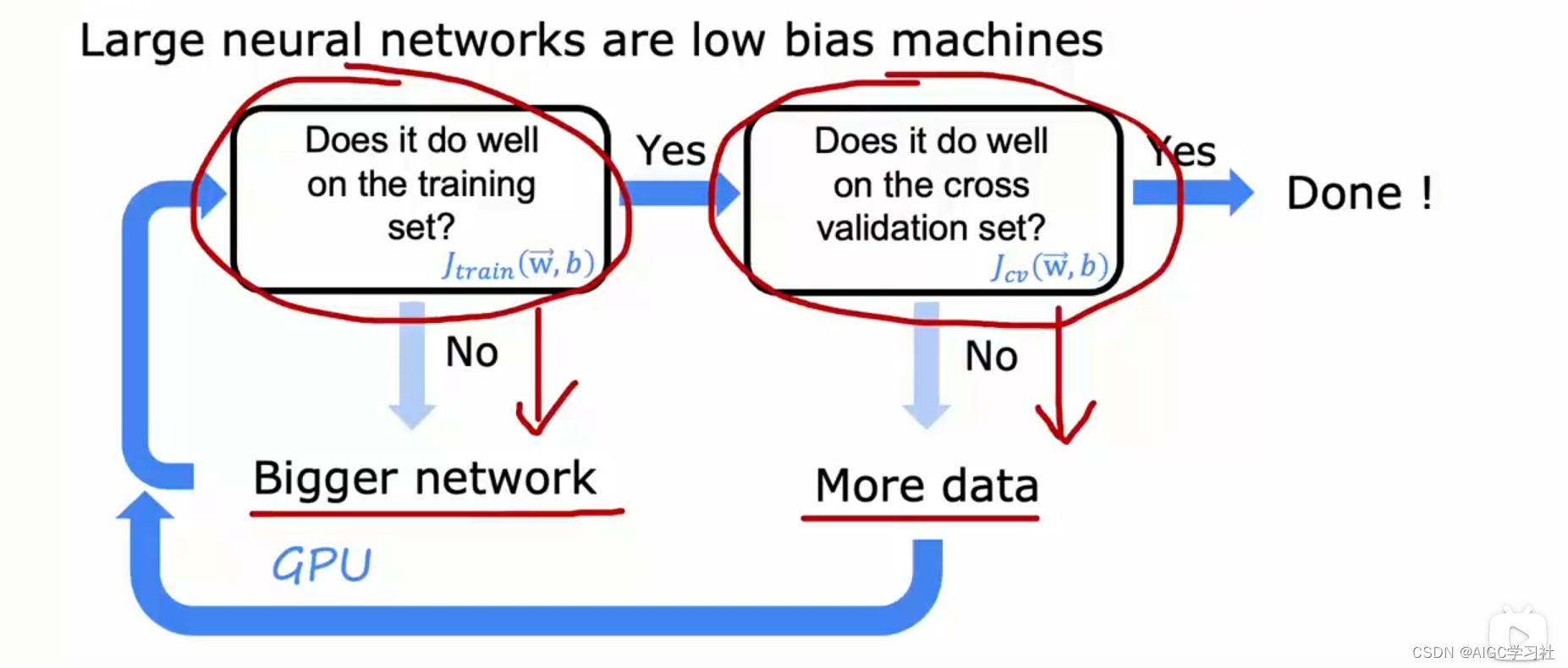
3.神经网络正则化
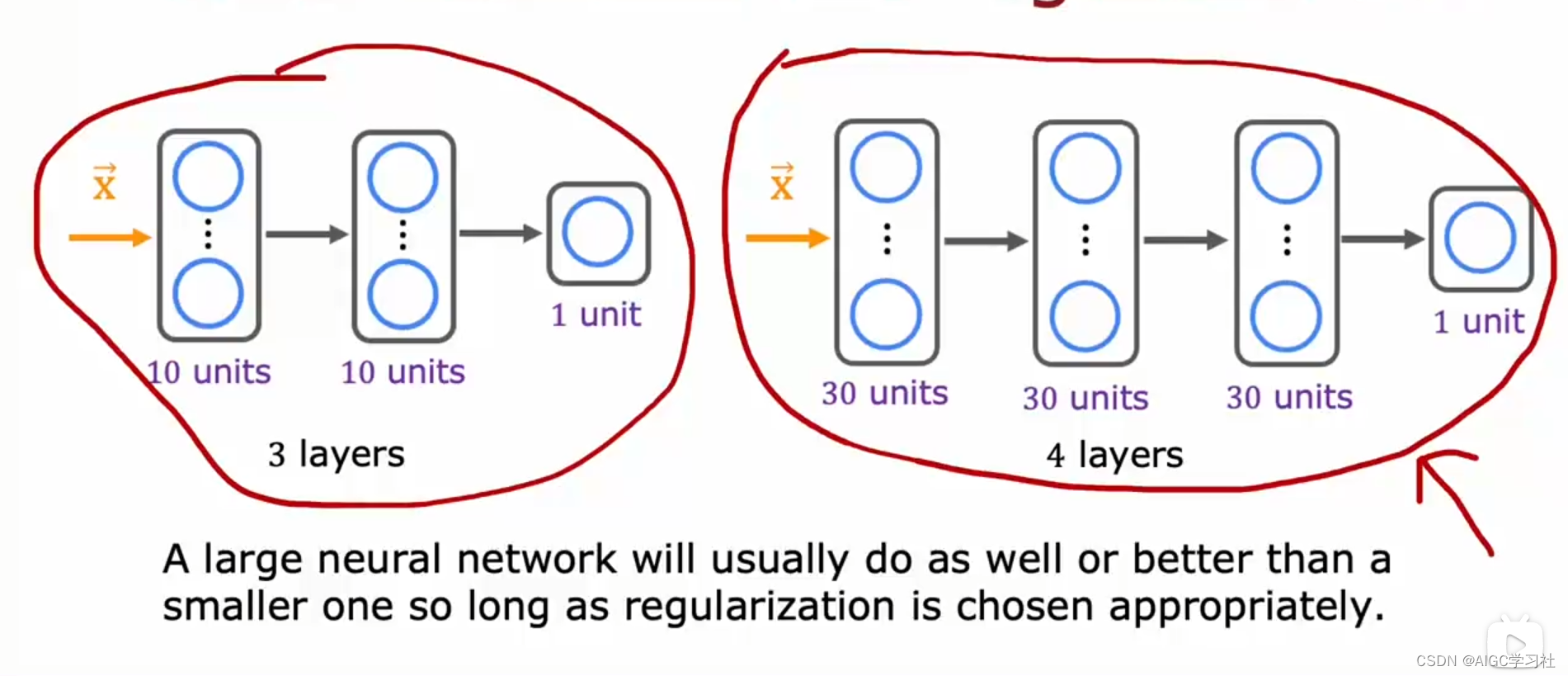
当训练神经网络时,选择合适的正则化方法后,大型神经网络通常比小型神经网络表现更好。虽然人们可能担心大型神经网络会导致高方差问题,但适当的正则化可以避免过拟合。唯一的缺点是大型神经网络会增加计算成本,减慢训练和推理过程。总体来说,适当正则化的大型神经网络几乎总是有益的。
神经网络如何正则化
代价函数可以是平方误差或逻辑损失,正则化项为 λ/2m × ∑w²,适用于所有权重w,通常不对参数b进行正则化。
在TensorFlow中实现正则化的方法是,在创建模型时添加kernel_regularizer=L2(0.01),其中0.01是λ的值。虽然可以为不同层选择不同的λ值,但通常为了简单起见,可以为所有层使用相同的λ值。这种方法可以在神经网络中实现正则化。

总结
- 只要正则化得当,更大的神经网络几乎不会带来负面影响,尽管可能会减慢算法速度,但通常不会影响性能,反而可能显著提升性能。
- 在训练集不太大的情况下,神经网络特别是大型神经网络通常是低偏差的,它们能够很好地拟合复杂函数,因此训练神经网络时主要解决的是方差问题而不是偏差问题。