🎩 欢迎来到技术探索的奇幻世界👨💻
📜 个人主页:@一伦明悦-CSDN博客
✍🏻 作者简介: C++软件开发、Python机器学习爱好者
🗣️ 互动与支持:💬评论 👍🏻点赞 📂收藏 👀关注+
如果文章有所帮助,欢迎留下您宝贵的评论,
点赞加收藏支持我,点击关注,一起进步!
目录
前言
正文
01-线图 (Plot)绘制
02-散点图 (Scatter Plot)绘制
03-条形图 (Bar Chart)绘制
04-饼图 (Pie Chart)绘制
05-3D曲面图 (3D Surface Plot)绘制
06-热图 (Heatmap)绘制
07-等高线图 (Contour Plot)绘制
总结
前言
Matlab 是一种强大的数值计算和技术计算环境,广泛应用于科学和工程领域。它提供了丰富的功能和工具,用于数据分析、可视化、算法开发、应用部署等多个方面。以下是 Matlab 的主要功能介绍:
数值计算与算法开发:
- Matlab 提供了高效的数值计算引擎,支持矩阵运算、线性代数、微积分等数学运算,适合处理大规模数据和复杂算法的开发与优化。
数据分析与可视化:
- 提供了丰富的绘图函数和工具箱,用于绘制各种类型的图表,包括线图、散点图、条形图、饼图、热图、等高线图等,帮助用户直观地分析和展示数据。
应用开发与部署:
- Matlab 支持开发独立的应用程序和图形用户界面(GUI),用于交互式数据分析和应用界面的设计。可以将 Matlab 代码部署为可执行文件或者集成到其他应用中。
信号处理与图像处理:
- 提供了专业的信号处理工具箱和图像处理工具箱,用于信号分析、滤波、频谱分析、图像增强、模式识别等应用。
控制系统设计与仿真:
- Matlab 在控制工程领域有着广泛的应用,提供了控制系统设计与分析的工具箱,支持系统建模、仿真和优化控制算法。
机器学习与深度学习:
- 针对机器学习和深度学习任务,Matlab 提供了专门的工具箱,包括分类、回归、聚类、神经网络等算法,支持数据预处理、模型训练和评估。
并行计算与大数据处理:
- Matlab 支持并行计算,通过并行计算工具箱和 GPU 加速,提高运行效率和处理大规模数据的能力。
数学建模与仿真:
- 提供了建模和仿真工具,用于模拟和分析动态系统、多物理场耦合系统等复杂系统的行为。
互操作性与集成:
- Matlab 可以与其他编程语言和工具集成,支持与 C/C++、Python、Java 的互操作性,扩展了应用场景和功能。
教育与学术研究:
- 在教育和学术研究中,Matlab 被广泛应用于教学、科研项目和学术论文的编写,为学生和研究人员提供强大的工具支持。
总体而言,Matlab 以其丰富的功能和用户友好的界面,成为科学计算和工程应用中的重要工具,广泛应用于学术、工业和商业领域。
正文
Matlab 提供了强大的绘图功能,支持多种类型的图形,包括但不限于:线图 (Plot)、散点图 (Scatter Plot):条形图 (Bar Chart):饼图 (Pie Chart):3D曲面图 (3D Surface Plot):热图 (Heatmap):等高线图 (Contour Plot):下面分别对其进行介绍:
01-线图 (Plot)绘制
线图绘制的代码如下所示:该段代码生成了正弦函数 (y = sin(x)) 的图像,其中包含以下解释:
-
绘图线条: 绘制了正弦曲线,线条宽度为 2,并使用特定的颜色。颜色通过 RGB 三元组
[0 114 189]/255定义,将 RGB 值转换为 MATLAB 中的标准颜色格式(值范围从 0 到 1)。这种颜色对应于一种蓝色 (#0072BD十六进制)。 -
标记点: 正弦曲线上的每个数据点都用大小为 6 的红色圆圈标记 (
'o') 标示。圆圈标记的填充颜色为红色 ('MarkerFaceColor', 'r')。 -
坐标轴标签和标题: x 轴标签为
x,y 轴标签为sin(x)。图像的标题为“Sine Function”,字体大小为 14。 -
网格线: 打开了图像的网格线 (
grid on),有助于更清晰地查看正弦函数在 x 轴上的数值变化。
x = 0:pi/100:2*pi; % 定义 x 的取值范围从 0 到 2*pi,步长为 pi/100 y = sin(x); % 计算 y 值,即 sin(x) figure; % 创建新的图形窗口 plot(x, y, 'LineWidth', 2, ... % 绘制 y 关于 x 的图像,并设置如下属性:'Color', [0 114 189]/255, ... % - 线条宽度为 2'Marker', 'o', ... % - 线条颜色使用 RGB 颜色 [0 114 189]/255'MarkerFaceColor', 'r', ... % - 标记点类型为 'o'(圆圈)'MarkerSize', 6); % - 标记点填充颜色为 'r'(红色),大小为 6 title('Sine Function', 'FontSize', 14); % 设置图像标题为“Sine Function”,字体大小为 14 xlabel('x', 'FontSize', 12); % 设置 x 轴标签为“x”,字体大小为 12 ylabel('sin(x)', 'FontSize', 12); % 设置 y 轴标签为“sin(x)”,字体大小为 12 grid on; % 显示图像网格线
x = 0:pi/100:2*pi;
y = sin(x);
figure;
plot(x, y, 'LineWidth', 2, 'Color', [0 114 189]/255, 'Marker', 'o', 'MarkerFaceColor', 'r', 'MarkerSize', 6);
title('Sine Function', 'FontSize', 14);
xlabel('x', 'FontSize', 12);
ylabel('sin(x)', 'FontSize', 12);
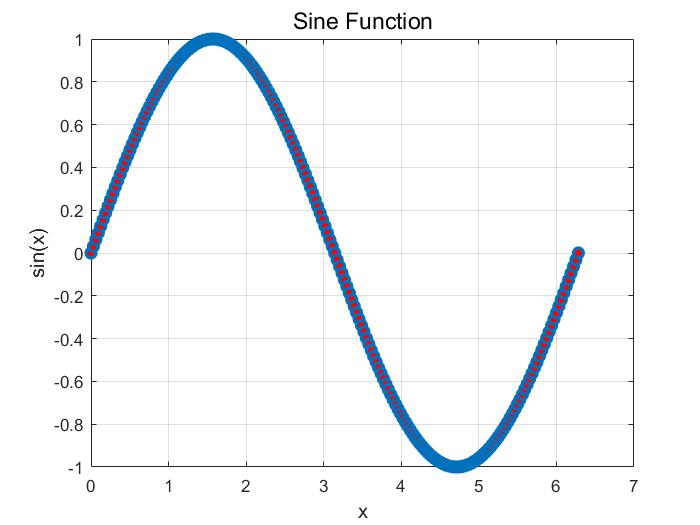
grid on;示例运行结果如下图所示:可视化输出
生成的图像直观地展示了正弦波形:
- 蓝色的线条形象地展示了从
0到2*pi范围内正弦函数的数值变化。 - 曲线上的每个点都由红色圆圈标记突出显示,这有助于准确查看这些点的数值。
- 坐标轴标签 (
x和sin(x)) 以及图像标题 (“Sine Function”) 提供了对绘制数据的背景和清晰的理解。 - 网格线进一步帮助读取图像中的数值变化。
02-散点图 (Scatter Plot)绘制
线图绘制的代码如下所示:
x = rand(1,100); % 生成包含100个随机数的向量作为 x 数据 y = rand(1,100); % 生成包含100个随机数的向量作为 y 数据figure; % 创建新的图形窗口 scatter(x, y, 50, 'filled', ... % 绘制散点图,并设置如下属性:'MarkerFaceColor', [217 83 25]/255); % - 标记点填充颜色为 RGB 颜色 [217 83 25]/255,即红色title('Scatter Plot', 'FontSize', 14); % 设置图像标题为“Scatter Plot”,字体大小为 14 xlabel('x', 'FontSize', 12); % 设置 x 轴标签为“x”,字体大小为 12 ylabel('y', 'FontSize', 12); % 设置 y 轴标签为“y”,字体大小为 12 grid on; % 显示图像网格线
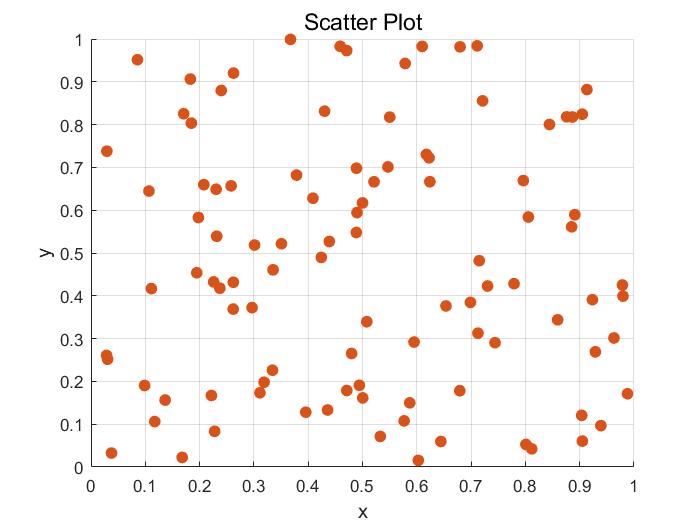
代码如下:这段代码生成了一个散点图,展示了随机生成的100个点的分布情况,具体说明如下:
-
散点图: 使用
scatter函数绘制了由x和y向量定义的散点图。每个点的大小为50个单位,使用了'filled'参数表示填充标记点。 -
标记点填充颜色: 标记点的填充颜色通过 RGB 颜色
[217 83 25]/255定义,这对应于一种红色 (#D95319十六进制)。在 MATLAB 中,RGB 值范围是从 0 到 1,因此需要将颜色值除以255进行归一化。 -
坐标轴标签和标题: x 轴标签为
x,y 轴标签为y。图像的标题为“Scatter Plot”,字体大小为 14。 -
网格线: 打开了图像的网格线 (
grid on),有助于更清晰地查看数据点的分布。
x = rand(1,100);
y = rand(1,100);figure;
scatter(x, y, 50, 'filled', 'MarkerFaceColor', [217 83 25]/255); % 使用RGB颜色表示法
title('Scatter Plot', 'FontSize', 14);
xlabel('x', 'FontSize', 12);
ylabel('y', 'FontSize', 12);
grid on; 运行结果如下:生成的图像直观地展示了随机生成数据点的分布情况:
- 每个点使用红色填充标记,大小为50个单位,突出显示了它们的位置和密度。
- 坐标轴标签 (
x和y) 和图像标题 (“Scatter Plot”) 提供了对绘制数据的背景和清晰的理解。 - 网格线进一步帮助读取图像中的数据点位置。
03-条形图 (Bar Chart)绘制
线图绘制的代码如下所示:
x = 1:5; % 创建一个包含从 1 到 5 的整数序列,作为 x 轴数据 y = [10 5 7 3 8]; % 创建一个包含 5 个数据点的向量,作为 y 轴数据figure; % 创建新的图形窗口 bar(x, y, 'FaceColor', [77 190 238]/255); % 绘制条形图,并设置如下属性:% - 条形的填充颜色为 RGB 颜色 [77 190 238]/255,即蓝绿色title('Bar Chart', 'FontSize', 14); % 设置图像标题为“Bar Chart”,字体大小为 14 xlabel('Category', 'FontSize', 12); % 设置 x 轴标签为“Category”,字体大小为 12 ylabel('Value', 'FontSize', 12); % 设置 y 轴标签为“Value”,字体大小为 12 grid on; % 显示图像网格线
这段 MATLAB 代码生成了一个简单的条形图,用于展示具有不同类别的值:
-
条形图: 使用
bar函数绘制了条形图,其中 x 轴表示类别,y 轴表示对应的值。共有 5 个类别,分别用整数序列 1 到 5 表示,对应的值分别为[10 5 7 3 8]。 -
填充颜色: 条形图的填充颜色通过 RGB 颜色
[77 190 238]/255定义,这对应于一种蓝绿色。在 MATLAB 中,RGB 值范围是从 0 到 1,因此需要将颜色值除以 255 进行归一化。 -
坐标轴标签和标题: x 轴标签为“Category”,y 轴标签为“Value”。图像的标题为“Bar Chart”,字体大小为 14。
-
网格线: 打开了图像的网格线 (
grid on),有助于更清晰地查看数据点的位置和条形的高度。
x = 1:5;
y = [10 5 7 3 8];
figure;
bar(x, y, 'FaceColor',[77 190 238] / 255);
title('Bar Chart', 'FontSize', 14);
xlabel('Category', 'FontSize', 12);
ylabel('Value', 'FontSize', 12);
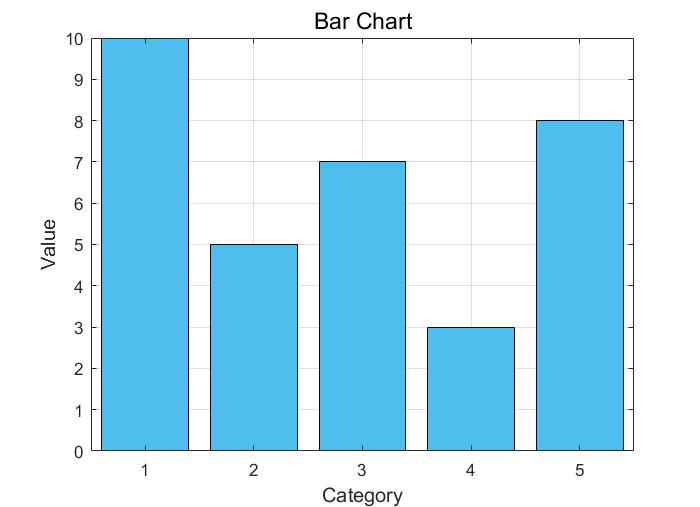
grid on;结果如下:
生成的图像直观地展示了不同类别的值:
- 每个条形的高度表示相应类别的值大小,分别为 10、5、7、3、8。
- 条形的填充颜色为蓝绿色,突出了条形图的视觉效果。
- 坐标轴标签和图像标题提供了对图像内容的清晰理解。
- 网格线进一步帮助读取图像中的数据点位置和条形的高度。
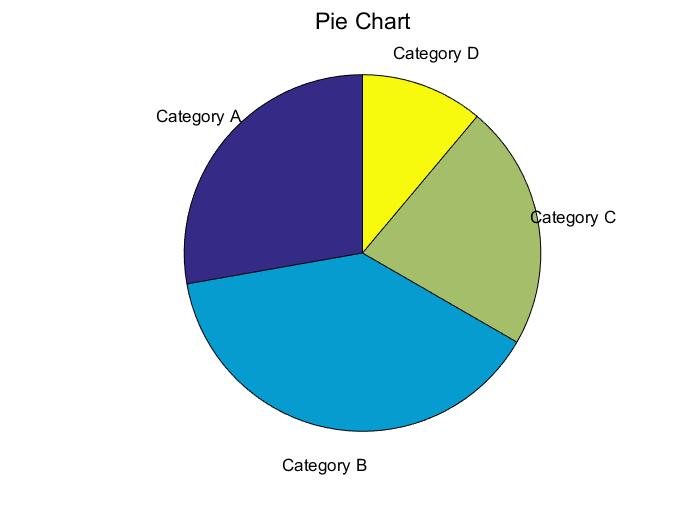
04-饼图 (Pie Chart)绘制
线图绘制的代码如下所示:
x = [25 35 20 10]; % 创建一个包含四个数值的向量作为饼图的数据 labels = {'Category A', 'Category B', 'Category C', 'Category D'}; % 创建一个包含标签的单元格数组figure; % 创建新的图形窗口 pie(x, labels); % 绘制饼图,并设置如下属性:% - 饼图数据为 x% - 饼图标签为 labelstitle('Pie Chart', 'FontSize', 14); % 设置图像标题为“Pie Chart”,字体大小为 14
这段 MATLAB 代码生成了一个简单的饼图,用于展示不同类别的相对比例:
-
饼图: 使用
pie函数绘制了饼图,其中x向量表示各个扇形的大小,即各类别的相对比例。在本例中,x = [25 35 20 10]表示了四个扇形的大小。 -
标签: 每个扇形的标签由
labels单元格数组定义,分别为 ‘Category A’, ‘Category B’, ‘Category C’, ‘Category D’。 -
图像标题: 设置了图像标题为“Pie Chart”,字体大小为 14,用以说明整个图的内容。
-
x = [25 35 20 10]; labels = {'Category A', 'Category B', 'Category C', 'Category D'}; figure; pie(x, labels); title('Pie Chart', 'FontSize', 14);
运行结果如下:
生成的饼图直观地展示了不同类别的相对比例:
-
每个扇形的大小反映了对应类别的相对比例。例如,‘Category B’ 的扇形最大,占据了整个饼图的最大部分,而 ‘Category D’ 的扇形最小。
-
扇形周围的标签 (‘Category A’ 到 ‘Category D’) 显示了各个类别的具体名称,使得整个图的含义更加清晰明了。
05-3D曲面图 (3D Surface Plot)绘制
线图绘制的代码如下所示:
[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2); % 创建 X 和 Y 的网格数据,范围为 -2 到 2,步长为 0.1
Z = X .* exp(-X.^2 - Y.^2); % 根据 X 和 Y 计算 Z 值,这里使用了一个简单的函数关系figure; % 创建新的图形窗口
surf(X, Y, Z, 'EdgeColor', 'none'); % 绘制三维表面图,并设置如下属性:% - X 为 X 轴数据% - Y 为 Y 轴数据% - Z 为 Z 轴数据% - 'EdgeColor', 'none' 表示不显示网格线条title('3D Surface Plot', 'FontSize', 14); % 设置图像标题为“3D Surface Plot”,字体大小为 14
xlabel('X', 'FontSize', 12); % 设置 x 轴标签为“X”,字体大小为 12
ylabel('Y', 'FontSize', 12); % 设置 y 轴标签为“Y”,字体大小为 12
zlabel('Z', 'FontSize', 12); % 设置 z 轴标签为“Z”,字体大小为 12这段 MATLAB 代码生成了一个简单的三维表面图,用于展示一个基于数学函数的曲面:
-
三维表面图: 使用
surf函数绘制了三维表面图。其中,X和Y是通过meshgrid函数生成的网格数据,Z是根据数学函数Z = X .* exp(-X.^2 - Y.^2)计算得出的表面高度。 -
曲面属性: 表面图的边缘颜色通过
'EdgeColor', 'none'设置为不显示,这样可以突出表面的形状而不受网格线的干扰。 -
坐标轴标签和标题: x 轴标签为“X”,y 轴标签为“Y”,z 轴标签为“Z”。图像的标题为“3D Surface Plot”,字体大小为 14。
[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = X .* exp(-X.^2 - Y.^2);
figure;
surf(X, Y, Z, 'EdgeColor', 'none');
title('3D Surface Plot', 'FontSize', 14);
xlabel('X', 'FontSize', 12);
ylabel('Y', 'FontSize', 12);
zlabel('Z', 'FontSize', 12);运行结果如下图所示
- 图像中的每个点
(X, Y, Z)表示在坐标(X, Y)处的高度Z。 - 表面的形状由函数的曲线特性决定,这里是一个带有指数衰减的 X 值乘积效应。
- 三维表面图提供了一种直观的方式来理解和分析数学函数的空间特性,非常适合用于科学计算和工程应用中的数据可视化。

06-热图 (Heatmap)绘制
线图绘制的代码如下所示:
data = rand(10); % 创建一个 10x10 的随机矩阵作为数据
figure; % 创建新的图形窗口
imagesc(data); % 绘制热力图,其中 data 是要绘制的矩阵数据
colormap(parula); % 设置颜色映射为 parula 色图
colorbar; % 添加颜色条,用于显示数据与颜色之间的对应关系
title('Heatmap', 'FontSize', 14); % 设置图像标题为“Heatmap”,字体大小为 14这段 MATLAB 代码生成了一个简单的热力图,用于可视化一个随机生成的 10x10 数据矩阵的数值分布情况:
-
热力图: 使用
imagesc函数绘制了热力图,其中data是一个 10x10 的随机矩阵。热力图的颜色深浅表示数据的相对大小,深色表示较小的值,浅色表示较大的值。 -
颜色映射: 通过
colormap(parula)设置了颜色映射为 parula 色图。Parula 是 MATLAB 默认的色图之一,它从蓝色到黄色的过渡,适合显示渐变和细节丰富的数据。 -
颜色条: 使用
colorbar函数添加了颜色条,颜色条显示了颜色与数据值之间的对应关系,帮助解释热力图中颜色的含义。 -
标题: 图像的标题为“Heatmap”,字体大小为 14,用以说明整个图的内容。
通过这种方式,可以直观地了解和分析数据矩阵的数值分布情况:
- 每个小方块的颜色深浅反映了对应位置的数据值大小,提供了一种视觉上的快速比较和分析方式。
- 颜色条帮助解释了颜色与数值之间的映射关系,使得热力图更具解释性和可读性。

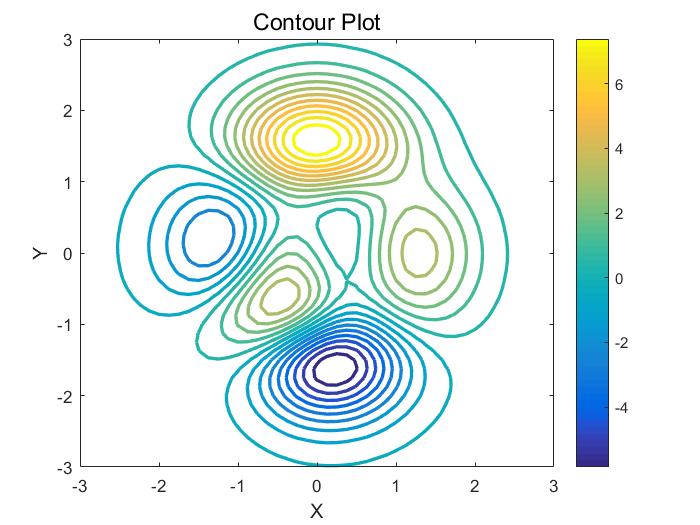
07-等高线图 (Contour Plot)绘制
线图绘制的代码如下所示:
[X, Y, Z] = peaks; % 使用 peaks 函数生成数据
figure; % 创建新的图形窗口
contour(X, Y, Z, 20, 'LineWidth', 2); % 绘制等高线图% - X 是等高线的 x 坐标% - Y 是等高线的 y 坐标% - Z 是等高线的 z 坐标% - 20 表示等高线的数量% - 'LineWidth', 2 表示等高线的线条宽度为 2title('Contour Plot', 'FontSize', 14); % 设置图像标题为“Contour Plot”,字体大小为 14
xlabel('X', 'FontSize', 12); % 设置 x 轴标签为“X”,字体大小为 12
ylabel('Y', 'FontSize', 12); % 设置 y 轴标签为“Y”,字体大小为 12
colorbar; % 添加颜色条,用于显示数据与颜色之间的对应关系这段 MATLAB 代码生成了一个简单的等高线图,用于展示一个二维曲面的轮廓:
-
等高线图: 使用
contour函数绘制了等高线图。等高线图是一种二维图形,用来表示三维空间中的曲面在不同高度上的轮廓线。 -
等高线参数: 参数
20表示在 Z 轴上绘制 20 条等高线,这使得等高线图更加详细和清晰。 -
等高线属性: 使用
'LineWidth', 2设置了等高线的线条宽度为 2,使得等高线更加明显。 -
坐标轴标签和标题: x 轴标签为“X”,y 轴标签为“Y”。图像的标题为“Contour Plot”,字体大小为 14。
-
颜色条: 使用
colorbar函数添加了颜色条,颜色条显示了颜色与数据
总结
以上就是Matlab 中常见的基本图形绘制方法及其用途。通过这些图形,可以直观地展示和分析数据,帮助研究人员和工程师理解数据的特征和趋势。