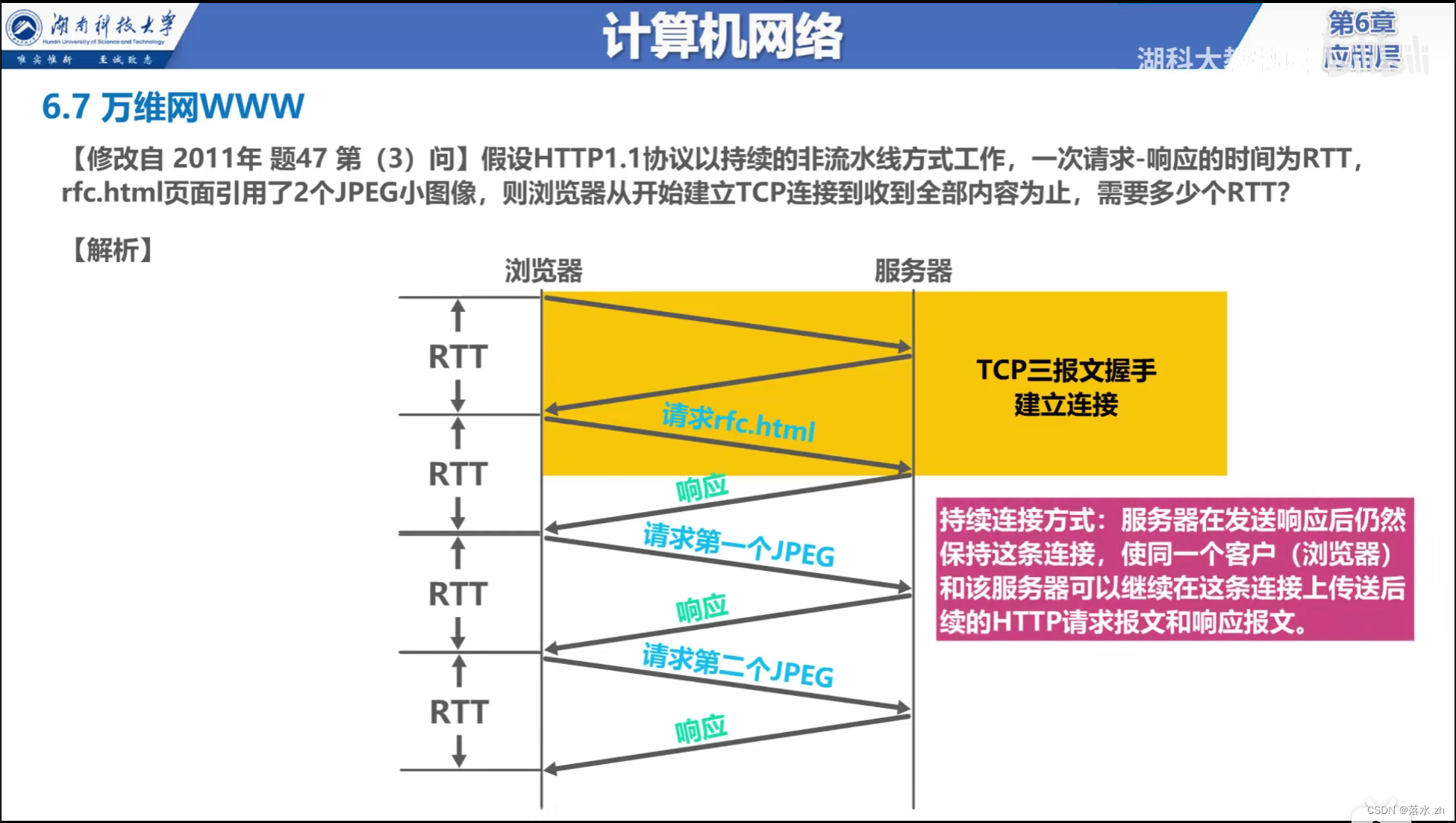
发生情况
定位到问题代码如下(脱敏处理过后),意思是集合排序,如果第一个元素大于第二个元素,比较结果返回1,否则返回-1,这里粗略的认为小于和等于是一样的结果
List<Integer> list = Arrays.asList(2213, 2214, 2235, 2211, 228, 2233, 2215, 2229, 2212, 0, 2245, 2220, 225,2237, 2241, 229,2221, 227, 2236, 226, 2246, 2222, 2247, 2232, 2240, 225, 2218, 2227, 2248, 2216, 2217, 2223);
list.sort((o1, o2) -> o1 > o2 ? 1 : -1);之前没问题啊,对 这个问题不是百分之百复现的,只需要将上述集合删除一些元素,报错就不会发生了看了一些人的文章,基本上意思是Collections.sort()在JDK6中使用的时MergeSort排序,在JDK1.7之后默认排序方式做了修改,使用TimeSort排序算法来排序,查看了一下Arrays.java源码,果然如此
public static <T> void sort(T[] a, Comparator<? super T> c) {if (c == null) {sort(a);} else {if (LegacyMergeSort.userRequested)legacyMergeSort(a, c);elseTimSort.sort(a, 0, a.length, c, null, 0, 0);}}- 自反性,x,y 的比较结果和 y,x 的比较结果相反,即compare(x, y) = - compare(y, x)
- 传递性,如果compare(x, y) > 0, compare(y, z) > 0, 则必须保证compare(x, z) > 0
- 对称性, 如果compare(x, y) == 0, 则必须保证compare(x, z) == compare(y, z)
基本解决
list.sort(new Comparator<Integer>() {@Overridepublic int compare(Integer integer, Integer anotherInteger) {return integer.compareTo(anotherInteger); //或者写成 return (x < y) ? -1 : ((x == y) ? 0 : 1);}
});或者直接用stream 流方式来排序就好,我也比较喜欢这种方式
// 升序
list=list.stream().sorted().collect(Collectors.toList());
// 降序
list=list.stream().sorted(Comparator.reverseOrder()).collect(Collectors.toList());探索底层报错原因
简述Timsort算法:
Timsort排序算法是一种结合了归并排序(merge sort)和插入排序(insertion sort)的高效排序算法,专为现实世界的数据排序需求而设计。TimSort 算法为了减少对升序部分的回溯和对降序部分的性能倒退,将输入按其升序和降序特点进行了分区。排序的输入的单位不是一个个单独的数字,而是一个个的块-分区。其中每一个分区叫一个run。针对这些 run 序列,每次拿一个 run 出来按规则进行合并。每次合并会将两个 run合并成一个 run。合并的结果保存到栈中。合并直到消耗掉所有的 run,这时将栈上剩余的 run合并到只剩一个 run 为止。这时这个仅剩的 run 便是排好序的结果。
基本思想:
- 利用现实数据中通常存在的部分已排序的特点,将数组拆分成多个已排序的分区(称为“run”)和未排序的分区。
- 对未排序的分区使用插入排序或其他方法进行排序,使其成为新的已排序分区。
- 最后,通过归并排序的思想将这些已排序的分区合并成一个完全有序的数组。
分区方法:
- 假定数据长度为n。
- 如果n小于某个阈值(如32或64,具体值可能因不同编程语言实现而异),则直接对整个数组使用插入排序或其他简单排序算法。
- 如果n大于或等于阈值,则先找到已排序的分区(run),并对这些分区进行标记。
- 如果分区是降序的,则将其翻转为升序。
合并规则:
- 使用一个栈来保存已排序的分区(run)。
- 从栈顶开始,按照归并排序的合并策略,将两个相邻的分区合并成一个更大的已排序分区。
- 合并的结果(新的已排序分区)继续压入栈中。
- 重复这个过程,直到栈中只剩下一个分区,此时整个数组已经排序完成。
特殊优化:
- Galloping模式:在合并过程中,使用一种称为“Galloping”的策略来快速跳过相等或接近相等的元素,从而提高合并效率。
- 二分插入排序:对于较小的分区(如长度小于阈值的分区),使用二分插入排序算法来提高排序效率
拆分RUN
那么首先看我们要排序的例子,正好32个,所以分为两个RUN,暂时成为 ra 和rb【划分的块数最好是完整二叉树的叶子节点的数量 即二的整数次幂(2,4,8...) 并且最好每个块要大小均匀而且维持在16到32之间的小块 这样效率最高 】
![]()
分别排序
那么接下来我们要做的就是分别讲ra 和rb 进行排序:
对整个List开始到结束单调递增或者单调递减的部分下标拿到,如果递增的则不变递减的把单调递减部分List反转 使其变为递增(java.util.ComparableTimSort#countRunAndMakeAscending) 然后以前段的单调递增List为基础 之后的元素一个个与前段基础List二分查找插入位置进行插入(java.util.ComparableTimSort#binarySort),最终结果得出。
对于上述,单调递增数据部分为 2213,2214,2235,所以结束的下标为3,所以得到基础递增部分,一次按着红色部分进行排序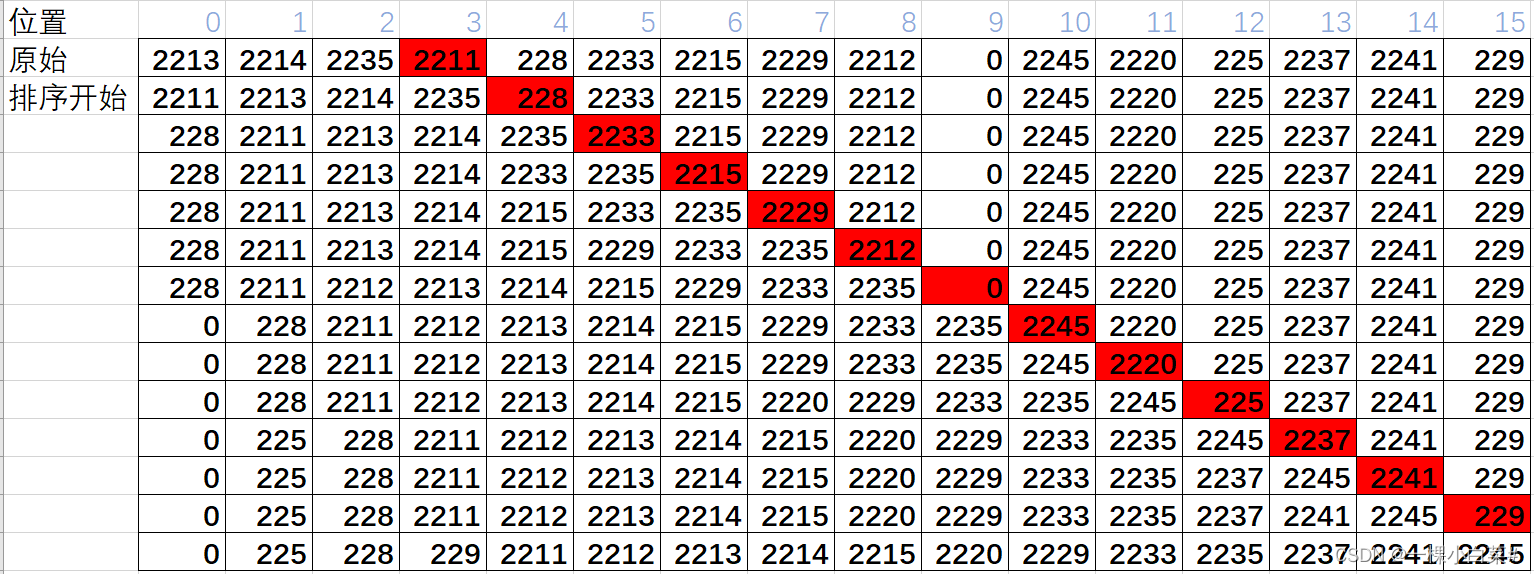
所以ra 最后得到排好的序列为 0 225 228 229 2211 2212 2213 2214 2215 2220 2229 2233 2235 2237 2241 2245
同理rb 最后得到排好的顺序为 225 226 227 2216 2217 2218 2221 2222 2223 2227 2232 2236 2240 2246 2247 2248
合并RUN
合并2个相邻的run需要临时存储空闲,临时存储空间的大小是2个run中较小的run的大小。Timsort算法先将较小的run复制到这个临时存储空间,然后用原先存储这2个run的空间来存储合并后的run
首先以ra 最大值2245去rb里面寻找位置,rb里面最小值到ra 寻找位置

这时候会发现绿色部分,已经不再需要我们再排序了,以为ra 绿色部分比rb 最小值还小,rb 的绿色部分比ra的最大值还大

那么需要我们进行排序的部分就是中间无底色部分,显然需要排序的rb所占有的元素更少些,那么所以把rb的数据做一个备份 temp 用一个大小为16的数组 因为备份的是rb 所以rb要先覆盖
所以我们得到如下

比较temp的2240 和ra的2245 ,我们得到了ra的2245>temp 的2240,这时候计数ra 连续胜利一次,并且把ra的2245 写入到rb的未排好序位置,排序后如下

比较temp的2240 和ra的2241,我们得到ra的2241> temp 的2240.计数ra 连续胜利一次,并且把ra的2241 写入到rb的未排好序位置,排序后如下

比较temp 的2240 和ra的2237,我们得到temp的2240 大于ra的2237,计数temp 连续胜利一次,并且把temp的2240 写入到rb的未排好序位置,排序后如下

比较temp 的2236 和ra的2237,我们得到ra的2237 大于temp的2236,计数ra 连续胜利一次,并且把ra的2237 写入到rb的未排好序位置,排序后如下

中间省略若干步骤.........
来看关键步骤吧

此时红色下划线部分都是ra原来的元素,所以呢ra七连胜了,此时触发了Galloping模式,这也就是这个程序报错的关键点了,只有触发了这个模式并且数据结构满足有两个相等情况,才会抛出异常Comparison method violates its general contract!
我们来看下为啥会出现矛盾呢?
在Timsort中,Galloping指的是一种在合并两个已排序的子序列(称为run)时,用于跳过不必要比较的策略,当算法试图将一个元素插入到另一个已排序的子序列中时,如果它发现当前元素小于子序列的第一个元素,它会继续向后搜索,直到找到一个合适的插入位置或到达子序列的末尾。这个过程中跳过多个元素的比较就称为Galloping。
在这里因为ra已经连续赢了7次,那么temp 的剩余元素225,226,227就直接用最小的225来对比ra的225了, 因为最初程序里的排序算法是 list.sort((o1, o2) -> o1 > o2 ? 1 : -1)
所以整体的下移到ra 黄色部分 得到

此时temp 全部排完了,但是temp的225确被排序到ra的225的右侧了,按我们之前的排序规则(o1, o2) -> o1 > o2 ? 1 : -1,225 对比225应该是返回-1, 所以temp的225应该是排在ra225的左边,所以程序自相矛盾了,抛出异常Comparison method violates its general contract!