第三章 线性模型

3.0 机器学习三要素

1. 模型：根据问题，确定假设空间
2. 策略：根据评价标准，确定选取最优模型的策略（通常会产出一个损失函数）
3. 算法：求解损失函数，确定最优模型。

3.1基本形式

线性模型（linear model）：试图学得一个通过属性的线性组合来进行预测的函数。
形式：
$$f(x)=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$$
向量表示：
$$f(x)=w^{T}x+b$$
其中，$w=(w_1;w_2;...w_d)$。
优势： 形式简单，易于建模，通过引入层级结构或高纬映射可得到非线性模型，可解释性强。
分类： 简单线性回归，多元线性回归。

3.2 线性回归

3.2.1模型

回归： 假设现在有一批数据点，我们用一条直线/曲线对这些点进行拟合，这个拟合过程就称为回归。
线性回归： 线性回归假设因变量 𝑌与自变量 𝑋之间存在线性关系。
一元线性回归： 在一元线性回归中，我们假设因变量 𝑌和自变量 𝑋之间存在一个线性关系，该关系可以用以下方程表示：

$$Y={\beta }_0+{\beta }_{1}X+ϵ$$

其中：

• 𝑌是因变量（目标变量）
• 𝑋是自变量（预测变量）
• ${\beta }_0$是截距（intercept），表示当自变量 X=0 时因变量 Y 的预期值。
• ${\beta }_1$是斜率（slope），表示自变量每增加一个单位，因变量的预期变化量。
• 𝜖是误差项（error term），表示模型无法解释的随机噪声。

多元线性回归： 在多元线性回归中，我们假设因变量 𝑌和多个自变量 $X_1,X_2,...,X_p$之间存在一个线性关系，该关系可以用以下方程表示：
$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+...+{\beta }_p{X}_p+ϵ$$
其中：

• Y是因变量
• $X_1,X_2,X_3$是自变量
• ${\beta }_0$是截距（intercept），表示当所有自变量 均为0时因变量 Y 的预期值。
• ${\beta }_1，{\beta }_2，...,{\beta }_p$是回归系数，表示每个自变量对因变量的影响程度。
• 𝜖是误差项（error term），表示模型无法解释的随机噪声。

3.2.2策略

在确定了问题的假设空间是线性空间后，我们就面临如何选取最优模型的策略，在目前的情况下就是去确定模型的参数。
最小二乘法： 最小二乘法（Least Squares Method, LSM）是一种统计方法，用于在数据拟合过程中找到最佳拟合函数，使得观测数据与拟合函数之间的误差平方和最小。广泛应用于回归分析中，用来估计模型参数。
极大似然估计法： 极大似然估计法（Maximum Likelihood Estimation, MLE）是一种用于估计统计模型参数的方法。其基本思想是通过最大化观测数据的似然函数，找到最有可能产生这些观测数据的参数值。
通过西瓜书和南瓜书的推导可以发现这两种方法是殊途同归的，最终得到如下所示的损失函数：
$$argmi{n}_{(w,b)}\sum _{i=1}^m(y_i-w{x}_i-b{)}^2$$

3.2.3求解w和b

基本的推导思路：

1. 证明$E_{(}w,b)={\sum }_{i=1}^m(y_i-w{x}_i-b{)}^2$是关于w和b的凸函数。
2. 用凸函数求最值的思路解出w和b。

在证明某个函数是凸函数之前先了解以下一些概念。
凸集： 设集合$D\subset {\mathbb{R}}^n$，如果对任意的$x,y\in D$与任意的$\alpha \in [0,1]$,有
$$\alpha x+(1-\alpha )y\in D$$
则称集合D是凸集。

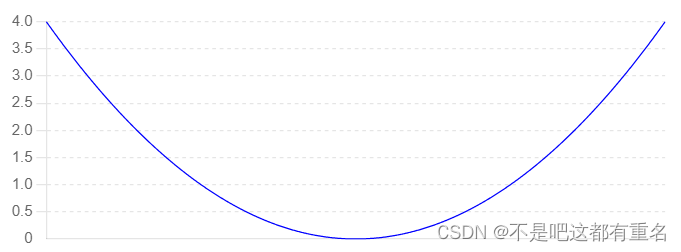
几何意义：若两个点属于此集合，则这两点连线上的任意一点均属于此集合。如下图所示就是个凸集。

凸函数： 设D是非空凸集，f是定义在D上的函数，如果对任意的$x^1$,$x^2$$\in D$,$\alpha \in (0,1)$,均有
$$f(\alpha x^1+(1-\alpha )x^2)\le \alpha f(x^1)+(1-\alpha )f(x^2)$$
则称$f$为D上的凸函数。如下图所示是一个典型的凸函数。

半正定矩阵：
定义：一个对称矩阵 A被称为半正定矩阵，当且仅当对于所有非零向量 𝑥，有 $x^{T}Ax\ge 0$换句话说，矩阵 𝐴的所有特征值都非负。

判定定理之一：若实对称矩阵的所有顺序主子式均为非负，则该矩阵为半正定矩阵。

**海塞矩阵：**对于一个标量值得多元函数$f(x_1,x_2,...x_n)$,海塞矩阵是由该函数得所有二阶偏导数组成得对称矩阵。海塞矩阵H的元素定义为：
$$H_{ij}=\frac{{\partial }^{2}f}{\partial x_i^2\partial x_j^2}$$
其中i,j=1,2,…,n。
海塞矩阵的形式化定义：

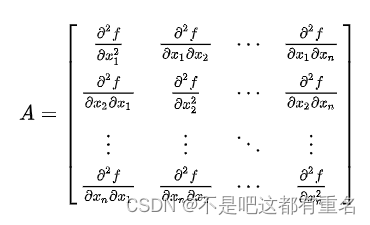
关键定理： 设$D\subset {\mathbb{R}}^n$是非空开凸集，$f:D\subset {\mathbb{R}}^n\to \mathbb{R}$，且f(x)在D上二阶连续可微，如果f(x)的Hessian（海塞）矩阵在D上是半正定的，则f(x)是D上的凸函数。

因此通过求损失函数的海塞矩阵是否为半正定的即可证明该损失函数为凸函数，然后即可用凸函数求最值的思路解出w和b。