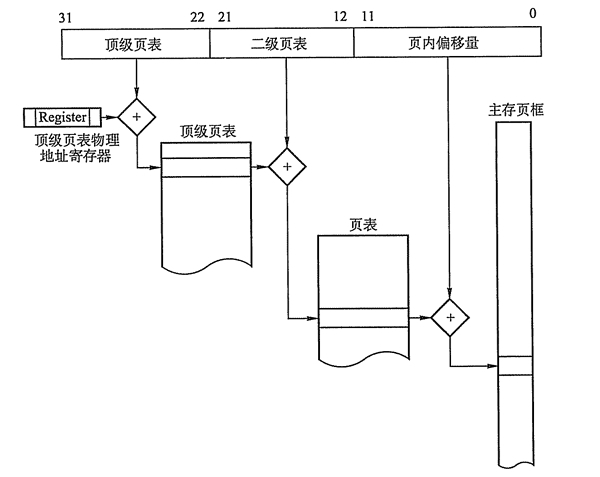
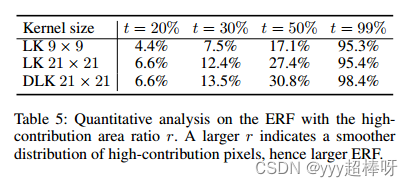
背包模型——AcWing 423. 采药

背包模型

定义

背包模型是一种常见的算法问题模型，它主要涉及将一些物品放入一个容量有限的背包中，以达到某种最优目标，如最大化价值或最小化重量等。

运用情况

常用于资源分配、项目选择、货物装载等实际问题中。例如，在选择要携带哪些物品进行旅行时，考虑物品的价值和重量以及背包的容量限制；或者在一些项目投资决策中，根据项目的收益和成本以及可用资金来进行最优选择。

注意事项

要明确物品的属性（价值、重量等）和背包的容量限制。
注意边界情况的处理，避免出现错误。
对于不同的约束条件和目标函数，需要选择合适的算法和策略。

解题思路

确定问题的状态，通常是背包的剩余容量和已选择的物品。
根据状态转移方程来计算最优解。
可能需要遍历所有物品和背包容量的不同情况来找到最终答案。

例如，假设有 3 个物品，重量分别为 2、3、4，价值分别为 3、4、5，背包容量为 5。那么通过逐步分析每个物品是否放入背包，来找到能使背包内价值最大的组合。

核心思想

一是在有限的资源（背包容量）约束下，通过对不同物品（具有一定的价值和占用一定的资源量）进行合理的选择和组合，以实现某种特定的最优目标，如价值最大化、利益最大化等。它强调了在资源有限的情况下做出最优决策的重要性。例如，在给定背包容量的情况下，要决定选择哪些物品放入背包才能使总价值达到最大。
二是通过分析不同物品的属性以及它们与背包容量的关系，来确定最佳的选择策略。这可能涉及到对每个物品的价值和资源占用进行权衡，以及考虑不同物品组合带来的效果。比如，可能需要比较选择某个物品所带来的价值增加与占用背包容量的代价，以决定是否将其放入背包。
三是运用动态规划等算法思想来高效地求解问题。通过逐步构建最优解的过程，从简单的情况逐步推导出复杂的情况，从而找到全局的最优解。举例来说，通过计算前几个物品在不同容量下的最优解，为后续物品的选择提供依据，逐步得到整个问题的最优解。

背包问题变体

0-1 背包问题：这是最基本的背包问题，每个物品只能选择一次，要么放入背包，要么不放入背包。
完全背包问题：在这个变体中，每个物品可以被无限次地选择放入背包。
多重背包问题：每个物品都有一个有限的数量，并且可以被选择多次，但不能超过其数量限制。
有界背包问题：每个物品的价值和重量都有上下界限制。
分数背包问题：物品可以被分割成任意部分，并且每个部分都有相应的价值和重量。
多维背包问题：将背包问题扩展到多个维度，例如考虑背包的体积、重量等多个因素。
动态背包问题：背包的容量或物品的数量在问题求解过程中是动态变化的。
随机背包问题：物品的价值或重量是随机的，需要考虑概率因素。
带约束的背包问题：除了背包容量的限制外，还有其他约束条件，如物品之间的兼容性、背包的数量限制等。
目标优化背包问题：除了最大化背包中物品的总价值外，还可以考虑其他目标，如最小化背包的重量、最大化物品的数量等。

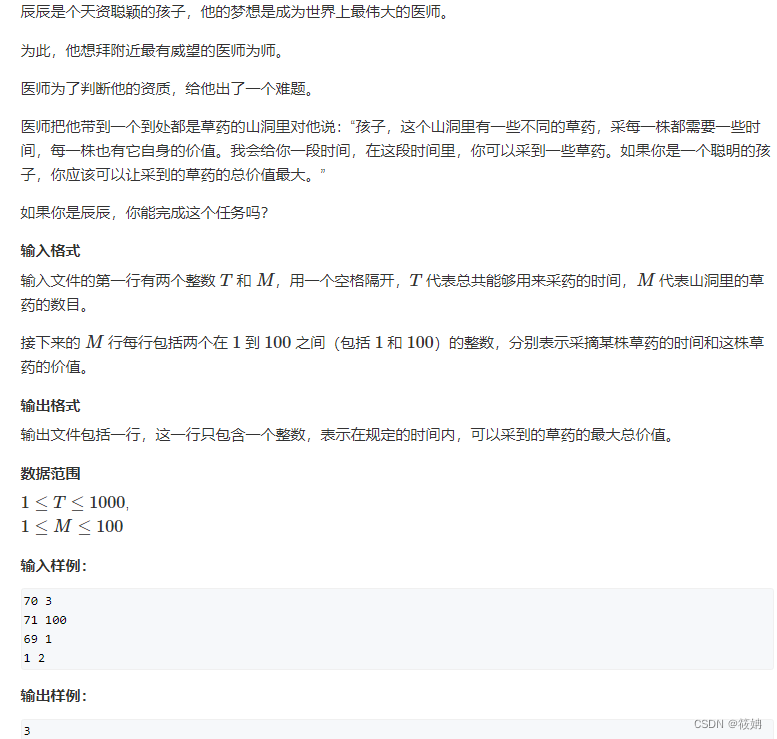
AcWing 423. 采药

题目描述

423. 采药 - AcWing题库

运行代码

#include <iostream>
#include <vector>
using namespace std;
int maxValue(int T, int M, vector<int>& times, vector<int>& values) {vector<vector<int>> dp(M + 1,vector<int>(T + 1, 0));for (int i = 1; i <= M; i++) {for (int t = 1; t <= T; t++) {if (times[i - 1] <= t) {dp[i][t] = max(dp[i - 1][t], dp[i - 1][t - times[i - 1]] + values[i - 1]);} else {dp[i][t] = dp[i - 1][t];}}}return dp[M][T];
}
int main() {int T, M;cin >> T >> M;vector<int> times(M);vector<int> values(M);for (int i = 0; i < M; i++) {cin >> times[i] >> values[i];}int result = maxValue(T, M, times, values);cout << result << endl;return 0;
}

代码思路

maxValue函数：
- 创建一个二维的 dp数组来进行动态规划计算。
- 通过两个嵌套的循环遍历所有可能的草药（i从 1 到 M）和时间（t从 1 到 T）。
- 对于每个草药和当前时间，如果当前草药的采摘时间小于等于当前可用时间，就比较不采摘该草药（即 dp[i-1][t]）和采摘该草药后用剩余时间去获取其他草药价值加上该草药本身价值（即 dp[i-1][t-times[i-1]]+values[i-1]），取较大值更新 dp[i][t]；如果采摘时间超过了可用时间，就直接继承上一轮该时间点的价值（即 dp[i-1][t]）。
- 最后返回 dp[M][T]，也就是在给定时间和草药情况下能获得的最大总价值。
main函数：
- 输入总的可用时间 T和草药的数量 M。
- 创建两个向量分别用于存储每个草药的采摘时间和价值。
- 通过循环读取每个草药的具体信息。
- 调用 maxValue函数计算并得到结果，最后输出。

其它代码

#include <iostream>using namespace std;const int N = 1010;int n, m;
int f[N];int main()
{cin >> m >> n;for(int i = 0; i < n; i ++ ){int v, w;cin >> v >> w;for(int j = m; j >= v; j -- ) f[j] = max(f[j], f[j - v] + w);}cout << f[m] << endl;return 0;
}

代码思路

定义了一个常量 N 用于表示一些固定的规模。
有两个变量 n 表示物品的数量，m 表示背包的容量。
定义了一个数组 f[N] 用于进行动态规划计算。
在 main 函数中：
- 首先输入背包容量 m 和物品数量 n。
- 然后通过一个循环依次输入每个物品的价值 v 和重量 w。
- 对于每个物品，再通过一个内层循环从背包容量 m 开始倒序遍历到当前物品的价值 v。在这个过程中，不断更新 f[j]，即判断当前背包容量为 j 时，不选该物品（即保持 f[j] 不变）和选择该物品（即 f[j - v] + w）哪种情况能得到更大的价值，取最大值更新 f[j]。这样就实现了在每个阶段根据已有的选择来确定最优的当前选择。
- 最后输出背包容量为 m 时对应的最大价值，也就是 f[m]。