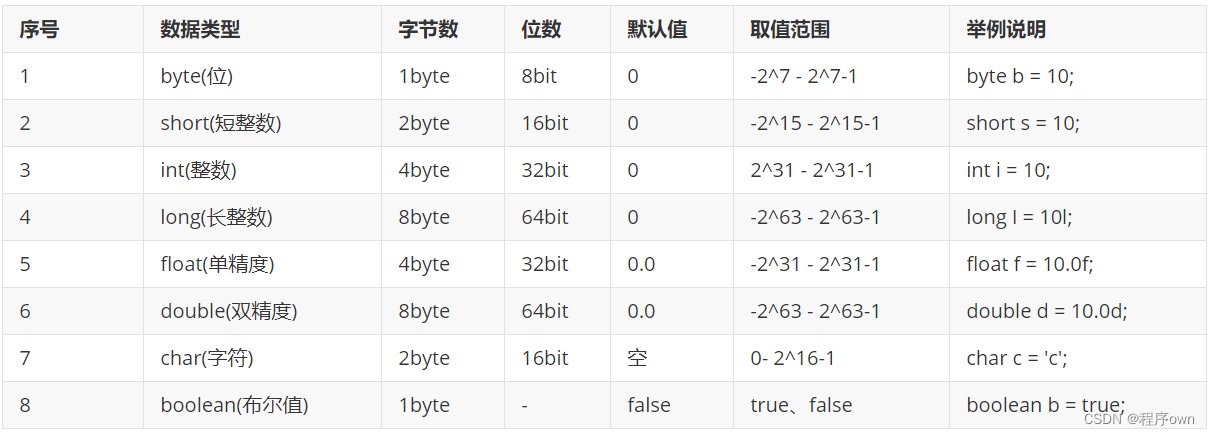
一个带权图n个点m条边，求起点到终点的最短距离

 先定义一个邻接矩阵graph，graph[i][j]表示从i到j的距离，i到j没有路就表示为无穷

然后定义一个visit数组，visit[i]表示i结点是否被访问

然后定义一个dist数组，dist[i]表示起点到i结点的最短距离

第一行输入n和m，表示有n个点m条边

接下来m行输入三个整数a，b，c，表示a到b存在一个距离为c的边

例如输入

4 4
0 1 500
0 2 100
1 3 200
1 2 300

图如下

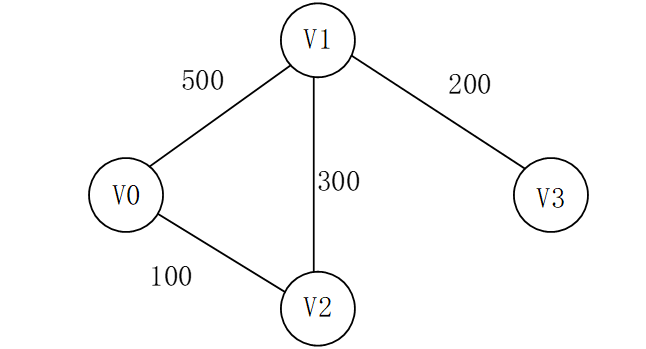
先初始化dist，初始值为起点到所有点的直达距离

dist={0,500,100,inf}，inf表示无穷，即不能直达

一开始起点被访问，所以visit初始化为

visit={1,0,0,0}

将除起点和终点外的每个点都作为中心节点并更新最短路径

一开始dist数组中{0,500,100,inf}最小值为100，对应的点为v2，所以将v2作为中心节点，令mid=2，再计算v2到所有未访问点的直达距离，更新dist，此时还有v1和v3未访问

dist变为{0,400,100,inf}

然后令visit[mid]=1表示已访问，依次类推，经过n-1轮后每个点visit位都为1，这个时候dist数组中dist[i]就表示起点到i结点的最短路径

#include<stdio.h>
#define inf 99999;	//定义99999为无穷大 
int dist[10];
int visit[10];
int graph[10][10];
int main(){scanf("%d%d",&n,&m);//先初始化所有边为无穷 for(i=0;i<n;i++){for(j=0;j<n;j++)graph[i][j]=inf;}//根据输入修改graghfor(i=0;i<m;i++){scanf("%d%d%d",&a,&b,&c);	//从a到b的距离为c graph[a][b]=c;graph[b][a]=c;	//由于是无向图，所以反过来也是c graph[i][i]=0;	//自己到自己距离为0}visit[0]=1;	//起点访问初始化为0 for(i=0;i<n;i++)dist[i]=graph[0][i];for(i=1;i<n;i++){//n个点需要n-1轮循环，因为一开始起点已经初始化了 //找dist数组最小值并记录下标为mid min_dist=inf;mid=0; for(j=0;j<n;j++){if((visit[j]==0) && (dist[j]<min_dist)){min_dist=dist[j];mid=j;}}//以mid为中心节点更新dist for(k=0;k<n;k++){if((visit[k]==0) && (dist[k]>dist[mid]+graph[mid][k])){dist[k]=dist[mid]+graph[mid][k];}}visit[mid]=1;//更新完后标记mid为访问 }for(i=0;i<n;i++)printf("%d ",dist[i]);	//输出起点到每个点的最短路径return 0;
}