前言
之前学过了其它的数据结构,如:
集合 \color{#5ecffd}集合 集合 —— 数据元素属于一个集合。
线型结构 \color{#5ecffd}线型结构 线型结构 —— 一个对一个,如线性表、栈、队列,每一个节点和其它节点之间的关系 一个对一个 \color{orange}一个对一个 一个对一个。
树型结构 \color{#5ecffd}树型结构 树型结构 —— 一个对多个,如树。
现在要接触一下图这个结构了,图是多个对多个的结构,其没有初始结点,也没有最终结点。每一个节点都称为顶点。
图 \color{#5ecffd}图 图——因为图是若干个顶点,顶点之间相互连接,没有先后顺序,所以图没有顺序存储结构,但可以借助二维数组来表示元素间的关系( 邻接矩阵 \color{orange}邻接矩阵 邻接矩阵)。链式存储结构也可以描述图: 邻接表、邻接多重表、十字链表 \color{orange}邻接表、邻接多重表、十字链表 邻接表、邻接多重表、十字链表。
邻接矩阵
存储表示:用两个数组分别存储 顶点表 \color{orange}顶点表 顶点表和 邻接矩阵 \color{orange}邻接矩阵 邻接矩阵。
#define MAZINT 32767 //极大值
#define MVNUM 100 //最大顶点数
typedef char VerTexType; //设顶点的数据类型为字符型
typedef int ArcType; //假设边的权值类型为整型typedef struct {VerTexType vexs[MVNUM]; //顶点表ArcType arcs[MVNUM][MVNUM]; //邻接矩阵int vexnum,arcnum; //图的当前点数和边数
}AMGraph;
图的定义和术语
Graph = (Vertex,Edge)
G = (V,E)
V:Vertex 顶点,描述:顶点数据有有穷非空集合。
E:Edge 边,描述:边的有空集合。
🚲有向图:每条边都是有方向的
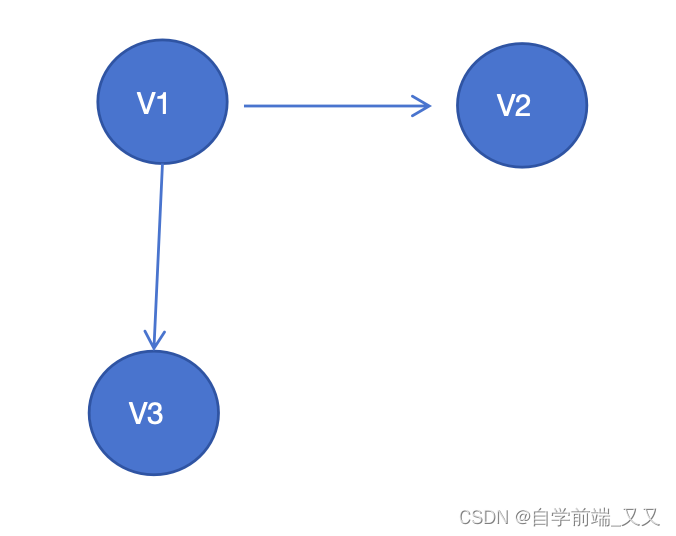
🚲无向图:每条边都是无方向的
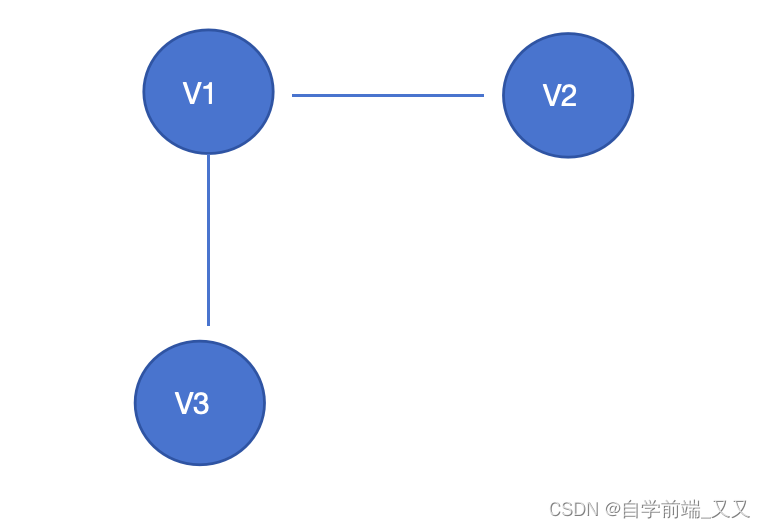
🚲无向完全图:其中任意一点,都和其余所有点相连接(无方向)。
V1 和 V2、V3、V4 相互连接
V2 和 V1、V3、V4 相互连接
V3 和 V1、V2、V4 相互连接
V4 和 V1、V2、V3 相互连接
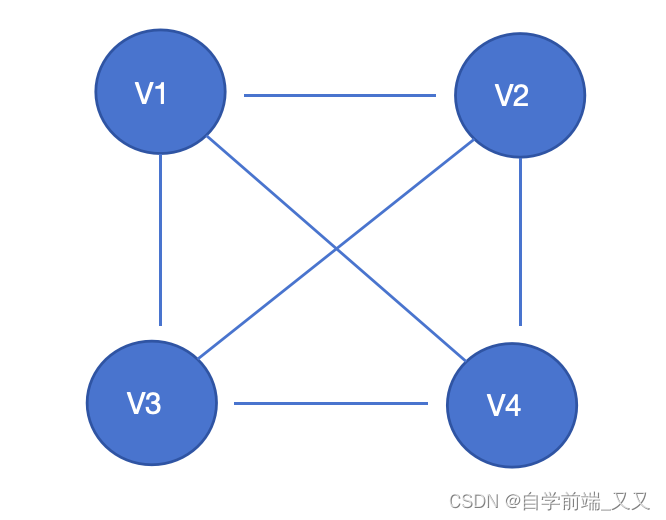
n 个顶点, n ( n − 1 ) / 2 条边 \color{orange}n个顶点,n(n-1)/2条边 n个顶点,n(n−1)/2条边
解释:(n-1):求单个顶点的最大边数
如果有A、B、C三个顶点
则A 的最大边数:A 和 B连,A 和 C 连。 = 2条(因为A无法和自己相连,所以单个顶点的最大边数 = 所有顶点数-自身 = n-1
解释:n(n-1):求所有顶点的最大边数之和
(n-1)为单个顶点的最大边数,乘以n 就为所有顶点的最大边数之和
解释:n(n-1)/2:边数
已经求出 n(n-1) 为所有顶点的最大边数之和,假设有三个顶点A、B、C。
A的最大边数为A 和 B连,A 和 C 连
B的最大边数为B 和 A连,B 和 C 连
可以看出来吗?第一次A和B连,第二次B和A连,其实重复了,边只有一个,但计算了两次。/2 的目的是为了消除所有单条边计算了两次的问题
🚲有向完全图:其中任意一点,都和其余所有点相连接(有方向)。
注意:有向图是每两个点有两条边相连,而不是一条双箭头的边
n 个顶点, n ( n − 1 ) 条边 \color{orange}n个顶点,n(n-1)条边 n个顶点,n(n−1)条边
V1 和 V2、V3、V4 相互连接
V2 和 V1、V3、V4 相互连接
V3 和 V1、V2、V4 相互连接
V4 和 V1、V2、V3 相互连接
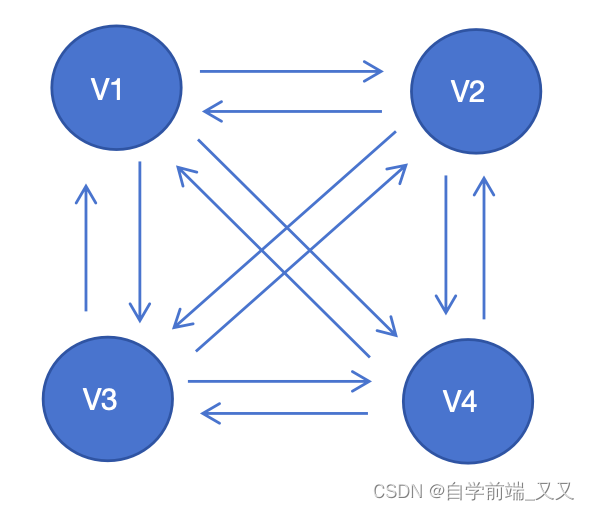
n 个顶点, n ( n − 1 ) 条边 \color{orange}n个顶点,n(n-1)条边 n个顶点,n(n−1)条边
解释:因为每两个顶点有两条边,把 /2去掉就行了。
🚲连通图
含义:所有的顶点都可以通过直接或间接的方式,到达任意一个顶点
无向图的连通图
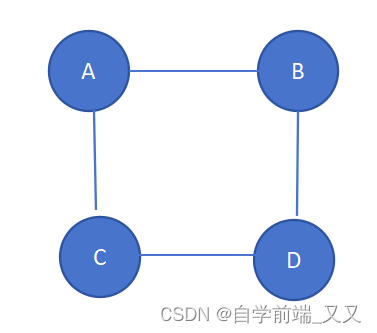
有向图的连通图
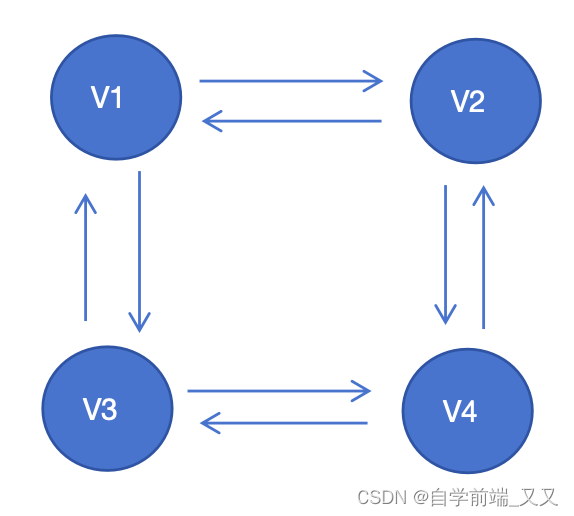
🚲非连通图
含义:有一个或大于一个的顶点,无法到达所有顶点,或无法被所有顶点到达任意一个顶点。
可以看到从V2无法到达任何一个顶点。
有向图的非连通图
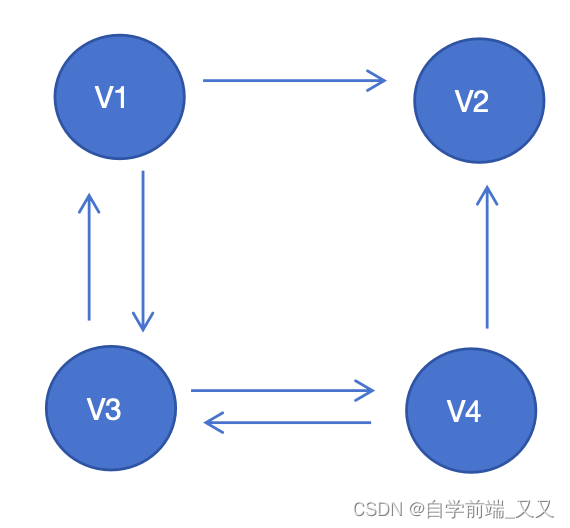
无向图的非连通图
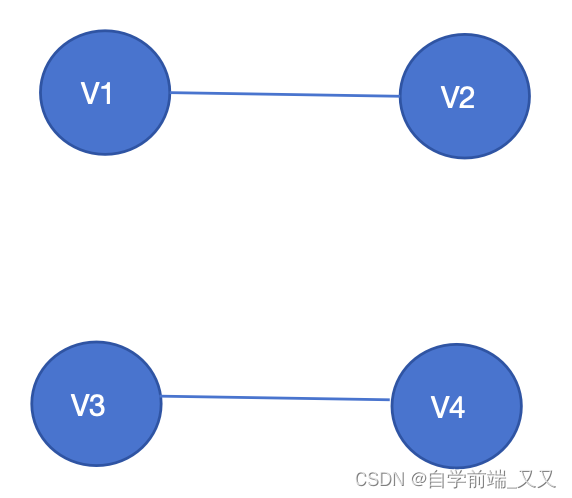
🛴有向图
稀疏图 \color{orange}稀疏图 稀疏图: 有很少边或弧的图(e < n l o g n n_{log}n nlogn)。
稠密图 \color{orange}稠密图 稠密图:有较多边或弧的图。
网 \color{orange} 网 网: 边/弧带权的图。
邻接 \color{orange}邻接 邻接:有边/弧相连的两个顶点之间的关系。
存在( V i , V j V_i,V_j Vi,Vj),则称 V i V_i Vi和 V j V_j Vj互为邻接点;
存在< V i , V j V_i,V_j Vi,Vj>,则称 V i V_i Vi邻接到 V j V_j Vj, V j V_j Vj邻接于 V i V_i Vi;
关联(依附) \color{orange}关联(依附) 关联(依附):边/弧与顶点之间的关系。
存在( V i , V j V_i,V_j Vi,Vj)/< V i , V j V_i,V_j Vi,Vj>,则称该边/弧关联于 V i 和 V j V_i和V_j Vi和Vj;
顶点的度 \color{orange}顶点的度 顶点的度:与该顶点相关联的边的数量,记为TD(V)
有向图的入度 \color{orange}有向图的入度 有向图的入度:其它顶点指向该顶点的边数。
有向图的出度 \color{orange}有向图的出度 有向图的出度:该顶点指向其它顶点的边数。
在 有向图 \color{orange}有向图 有向图中,顶点的度为该顶点的 入度 \color{orange}入度 入度和 出度 \color{orange}出度 出度的和。
路径 \color{orange}路径 路径:连接的边构成的顶点序列。
路径长度 \color{orange}路径长度 路径长度:路径上 (边或弧的数目/权值之和)。
回路 ( 环 ) \color{orange}回路(环) 回路(环):第一个顶点和最后一个顶点相同的路径。
简单路径 \color{orange}简单路径 简单路径:除路径起点和终点可以相同,其余顶点均不相同的路径。
简单路径 ( 简单环 ) \color{orange}简单路径(简单环) 简单路径(简单环):除路径起点和终点相同外,其余顶点均不相同的路径。
权 \color{orange}权 权:图中边或弧所具有的相关数称为权。表明从一个顶点到另一个顶点的距离或耗费。
网 \color{orange}网 网:带权的图称为网。
子图 \color{orange}子图 子图:设有两个图G=(V,{E})、G1=(V1,{E1})、若 V 1 ∈ V , E 1 ∈ E , 则称 G 1 是 G 的子图。 V1\in V,E1 \in E,则称G1是G的子图。 V1∈V,E1∈E,则称G1是G的子图。
极大连通子图 \color{orange}极大连通子图 极大连通子图:该子图是G的连通子图,将G图分成多个子图,其中一个子图每个顶点都可以连接,若将一个子图中的顶点移入到该子图,则该子图的这个顶点无法与任意一个顶点相互连通,则称该子图为极大连通子图。
连通分量(强连通分量) \color{orange}连通分量(强连通分量) 连通分量(强连通分量):无向图G的极大连通子图称为G的连通分量。
极小连通子图 \color{orange}极小连通子图 极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边,则该子图不再连通。
生成树 \color{orange}生成树 生成树:包含无向图G所有顶点的极小连通子图。
生成森林 \color{orange}生成森林 生成森林:对非连通图,由各个连通分量的生成树的集合。
图的操作
CreateGraph(*G,V,VR)
初始条件: V是图的顶点集,VR是图中弧的集合。
操作结果:按V和VR的定义 构造图 G \color{orange}构造图G 构造图G
DFSTraverse(G)
初始条件: 图G存在。
操作结果:对图进行 深度优先遍历 \color{orange}深度优先遍历 深度优先遍历
BFSTraverse(G)
初始条件: 图G存在。
操作结果:对图进行 广度优先遍历 \color{orange}广度优先遍历 广度优先遍历


![[论文阅读笔记33] Matching Anything by Segmenting Anything (CVPR2024 highlight)](https://img-blog.csdnimg.cn/direct/af9ef3cfc1734d39bab2c1aa3df9f670.png)