1、一维和二维自组织映射原理
一维和二维自组织映射(Self-Organizing Maps, SOM)是一种无监督的机器学习算法,通过学习输入数据的拓扑结构,将高维输入数据映射到低维的网格结构中,使得相似的输入数据点在映射空间中也会彼此靠近。一维和二维SOM算法的原理如下:
-
初始化网络:首先,随机初始化一个具有一定结构的网络,通常为一维或二维的网格结构,每个节点都代表一个权重向量。
-
训练网络:通过迭代的方式,将输入数据通过与网络中的节点计算距离,将最接近的节点称为获胜节点(winner node),并更新获胜节点及其邻近节点的权重向量,使得它们更好地表示输入数据。
-
衰减学习率:在训练过程中,逐渐减小学习率和邻域半径,使得网络在接近收敛时对输入数据的调整更加小步长和局部。
-
完成训练:当网络收敛或迭代次数达到预设值时,训练过程结束,此时网络中的节点已经学习到了输入数据的拓扑结构。
通过以上原理,一维和二维自组织映射算法可以用于降维、聚类、可视化等领域的数据分析和模式识别任务中。
2、一维自组织映射
1)说明
二维层中的神经元可学习表示输入向量在输入空间出现的不同区域。此外,邻近的神经元可学习对相似的输入进行响应,从而该层可学习所呈现的输入空间的拓扑。
2)数据集
创建了位于单位圆上的 100 个数据点。
竞争网络将用于将这些点分成若干自然类。
代码
angles = 0:0.5*pi/99:0.5*pi;
X = [sin(angles); cos(angles)];
figure(1)
plot(X(1,:),X(2,:),'+r')视图效果
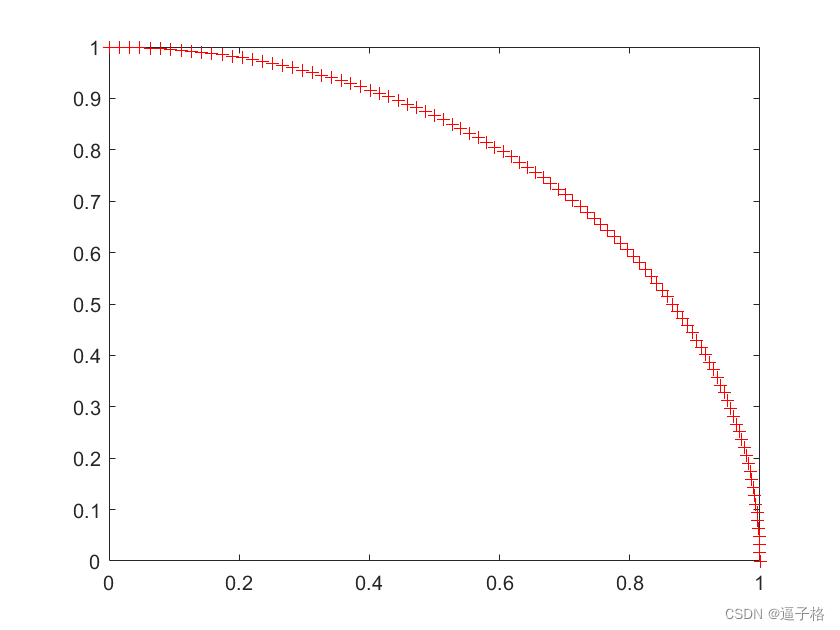
3)映射将是由 10 个神经元组成的一维层。
代码
net = selforgmap(10);
4)网络训练
说明:指定网络将接受 10 轮训练,并使用 train 基于输入数据对网络进行训练。
代码
net.trainParam.epochs = 10;
net = train(net,X);视图效果
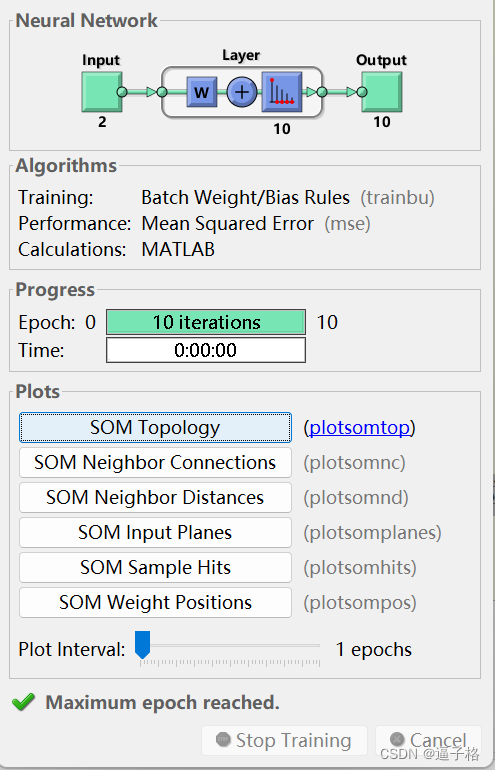
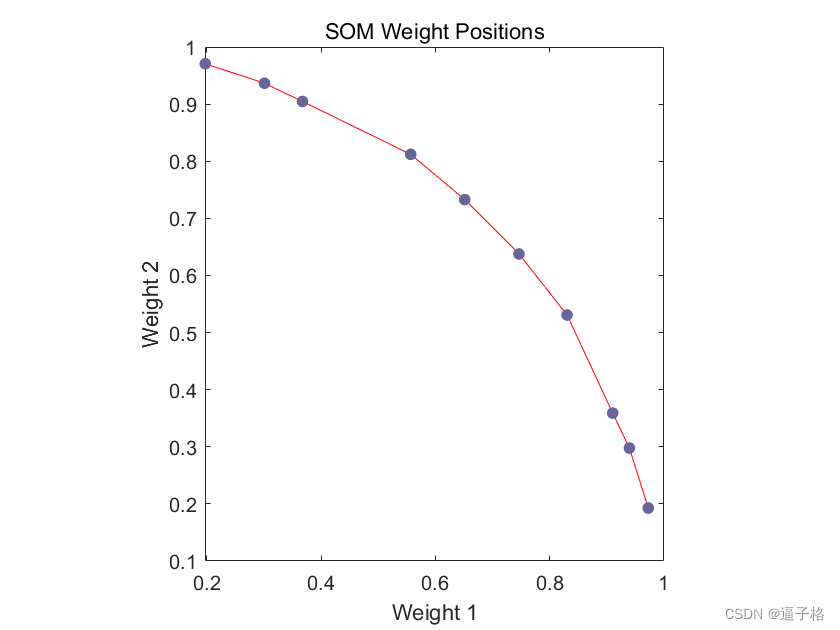
5)使用 plotsompos 绘制经过训练的网络的权重位置。
说明:红点是神经元的权重向量,蓝线连接在距离 1 内的每对红点。
代码
figure(2)
plotsompos(net)试图效果
6) 对输入进行分类
说明:映射可用于对输入进行分类,例如 [1; 0]。神经元 1 或 10 的输出应该为 1,因为上述输入向量位于所呈现的输入空间的一端。第一对数字表示神经元,单个数字表示其输出。
代码
x = [1;0];
a = net(x)a =0000000000000000000000000100003、 二维自组织映射
1)说明
自组织映射将学习表示输入向量在输入空间中出现的不同区域
神经元会形成二维网格,对一个矩形中的 1000 个二元素向量进行分类
2)输入数据
代码
X = rands(2,1000);
figure(3)
plot(X(1,:),X(2,:),'+r')视图效果
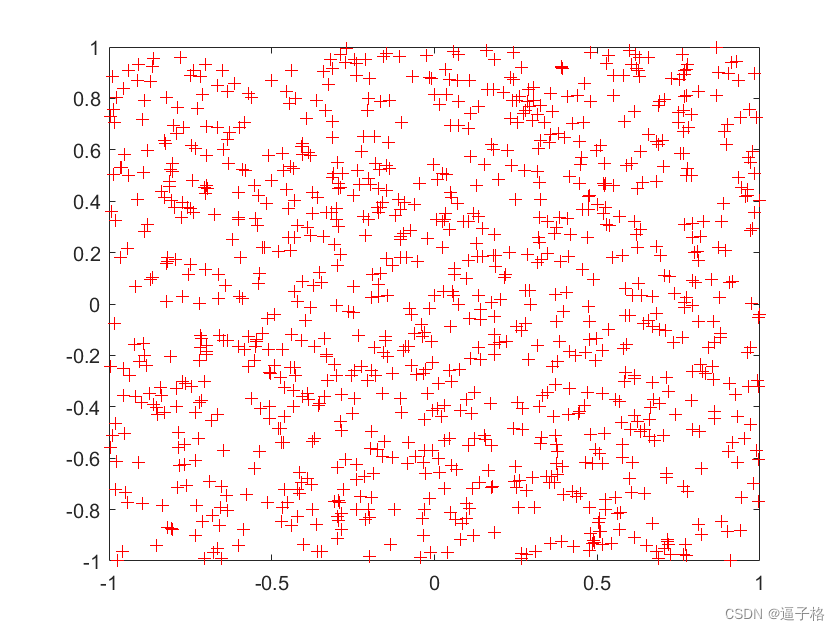
3) 使用 5×6 神经元层对上述向量进行分类
说明:每个神经元对矩形的不同区域作出响应,相邻神经元对相邻区域作出响应。将网络配置为匹配输入的维度
代码
net = selforgmap([5 6]);
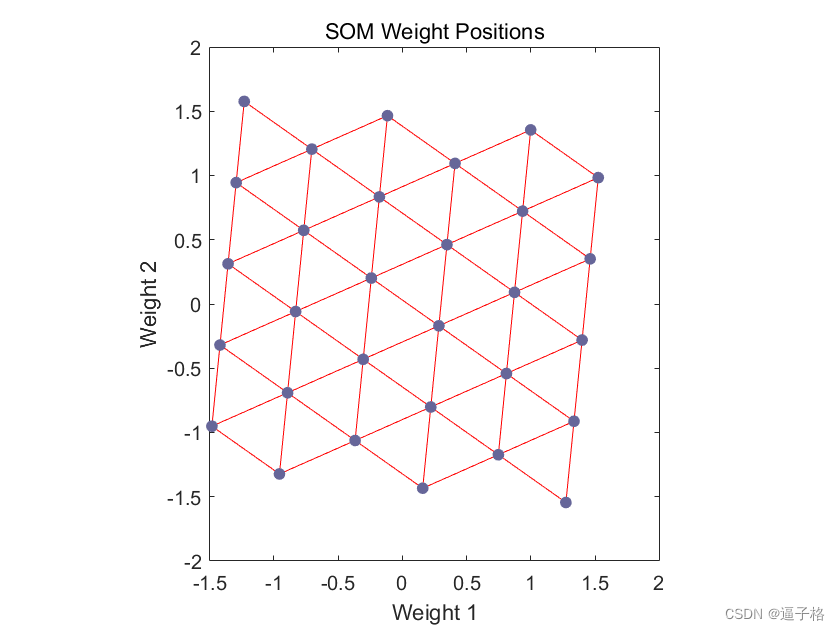
net = configure(net,X);4) 使用 plotsompos 可视化创建的网络。
说明:每个神经元在其两个权重的位置用红点表示。最初,所有神经元的权重相同,位于向量的中间,因此只出现一个点。
代码
figure(4)
plotsompos(net)视图效果
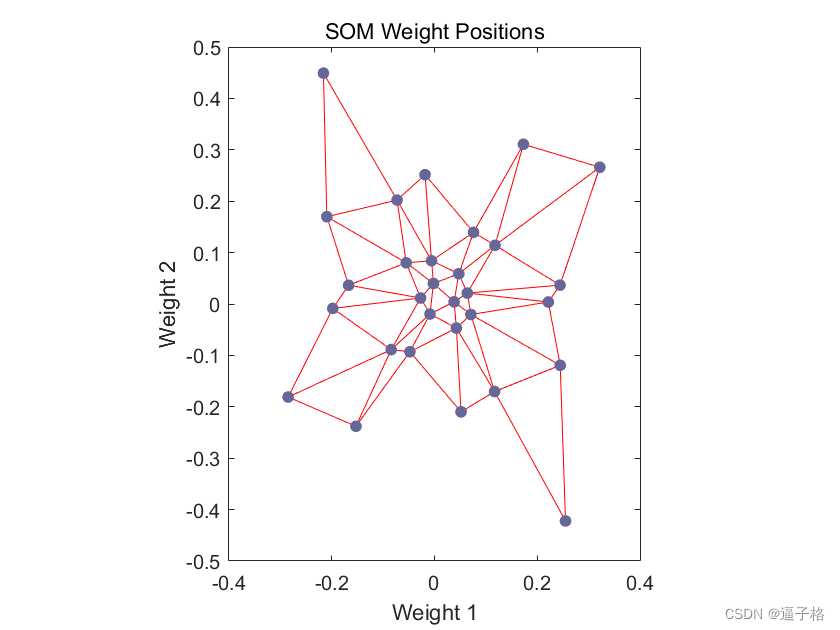
5) 训练网络
说明:训练后,神经元层已开始自组织,每个神经元现在界定输入空间的不同区域,并且相邻(连接的)神经元对相邻区域作出响应。
代码
figure(5)
net.trainParam.epochs = 1;
net = train(net,X);
plotsompos(net)视图效果
6) 向量输入网络并观察哪个神经元有响应来对向量进行分类
说明:由“1”表示的神经元有响应,因此 x 属于该类。
代码
x = [0.5;0.3];
y = net(x)4、总结
使用MATLAB实现一维和二维自组织映射(SOM)可以通过使用MATLAB的 Neural Network Toolbox 来实现。以下是一维和二维自组织映射的主要步骤和示例代码:
1数据准备:首先,准备输入数据集并进行必要的预处理。
2创建SOM网络:使用 MATLAB 的 selforgmap 函数来创建一维或二维自组织映射网络。例如:
som = selforgmap([8 8]); % 创建一个 8x8 的二维SOM网络3训练网络:使用 train 函数来训练SOM网络。例如:
[net, tr] = train(som, data);4可视化结果:可以使用 plotsomhits 函数来可视化SOM网络的节点之间的距离。例如:
plotsomhits(som, data);5使用SOM网络进行预测:使用 MATLAB 的 sim 函数来使用训练好的SOM网络进行数据映射。例如:
output = sim(som, new_data);总的来说,使用 MATLAB 实现一维和二维自组织映射是比较简单和直观的,只需要利用 Neural Network Toolbox 提供的函数和工具即可轻松完成。通过训练SOM网络,可以实现数据降维、可视化、聚类等应用。
5、源代码
代码
%% 一维自组织映射
%二维层中的神经元可学习表示输入向量在输入空间出现的不同区域。此外,邻近的神经元可学习对相似的输入进行响应,从而该层可学习所呈现的输入空间的拓扑。
%% 数据集
%创建了位于单位圆上的 100 个数据点。
%竞争网络将用于将这些点分成若干自然类。
angles = 0:0.5*pi/99:0.5*pi;
X = [sin(angles); cos(angles)];
figure(1)
plot(X(1,:),X(2,:),'+r')
%映射将是由 10 个神经元组成的一维层。
net = selforgmap(10);
%网络训练
%指定网络将接受 10 轮训练,并使用 train 基于输入数据对网络进行训练。
net.trainParam.epochs = 10;
net = train(net,X);
%使用 plotsompos 绘制经过训练的网络的权重位置。
%红点是神经元的权重向量,蓝线连接在距离 1 内的每对红点。
figure(2)
plotsompos(net)
%对输入进行分类
%映射可用于对输入进行分类,例如 [1; 0]。神经元 1 或 10 的输出应该为 1,因为上述输入向量位于所呈现的输入空间的一端。第一对数字表示神经元,单个数字表示其输出。
x = [1;0];
a = net(x)
%% 二维自组织映射
%自组织映射将学习表示输入向量在输入空间中出现的不同区域
%神经元会形成二维网格,对一个矩形中的 1000 个二元素向量进行分类
%输入数据
X = rands(2,1000);
figure(3)
plot(X(1,:),X(2,:),'+r')
%使用 5×6 神经元层对上述向量进行分类
%每个神经元对矩形的不同区域作出响应,相邻神经元对相邻区域作出响应。将网络配置为匹配输入的维度
net = selforgmap([5 6]);
net = configure(net,X);
%使用 plotsompos 可视化创建的网络。
%每个神经元在其两个权重的位置用红点表示。最初,所有神经元的权重相同,位于向量的中间,因此只出现一个点。
figure(4)
plotsompos(net)
%训练网络
%训练后,神经元层已开始自组织,每个神经元现在界定输入空间的不同区域,并且相邻(连接的)神经元对相邻区域作出响应。
figure(5)
net.trainParam.epochs = 1;
net = train(net,X);
plotsompos(net)
%向量输入网络并观察哪个神经元有响应来对向量进行分类
%由“1”表示的神经元有响应,因此 x 属于该类。
x = [0.5;0.3];
y = net(x)