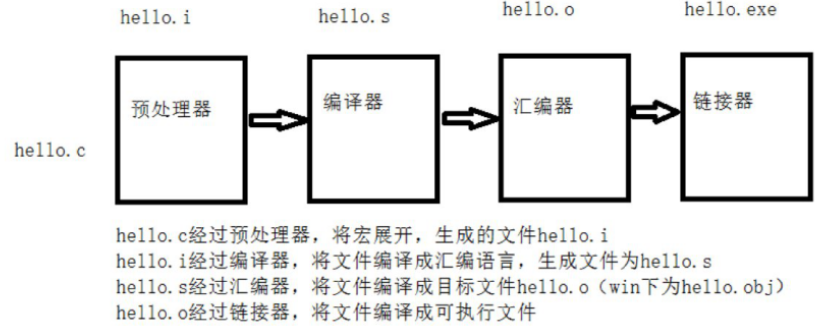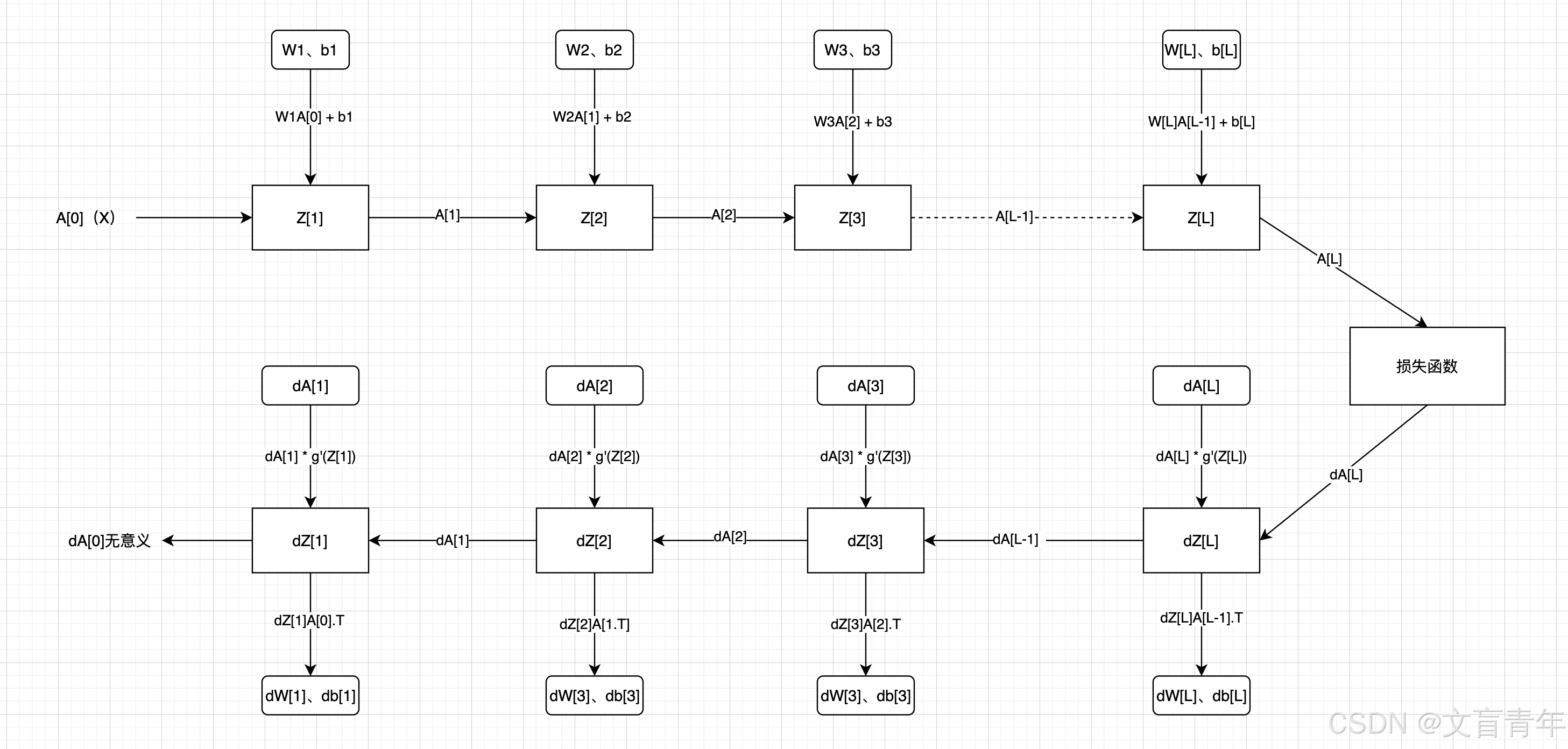
维度说明：

A[L]、Z[L]：（本层神经元个数、样本数）
W[L]：（本层神经元个数、上层神经元个数）
b[L]：（本层神经元个数、1）

dZ[L]：dA[L] * g’A（Z[L]）
dZ[L]：（本层神经元个数、样本数）
dw = dL/dz * dz/dw = dz*x（链式法则）
db = dz（链式法则）
dW[L]：（本层神经元个数、上层神经元个数）
dA[L]：（本层神经元个数、样本数）
da = dz * w
dA[L-1] = W[L].T dZ[L]，注意这里没有除以神经元个数，得到平均da。比如结果的第一个元素是多个dw1 * dz + dw1 * dz+ …dw1 * dz（神经元个数）的累加和

输出层采用sigmoid，隐藏层采用tanh

import numpy as np
# 设置一些画图相关的参数
import matplotlib.pyplot as pltplt.rcParams['figure.figsize'] = (5.0, 4.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
from project_03.utils.dnn_utils import *
from project_03.utils.testCases import *def load_dataset():train_dataset = h5py.File('../deep_learn_01/project_01/datasets/train_catvnoncat.h5', 'r')train_set_x_orig = np.array(train_dataset['train_set_x'][:])train_set_y_orig = np.array(train_dataset["train_set_y"][:])  # 加载训练数据test_dataset = h5py.File('../deep_learn_01/project_01/datasets/test_catvnoncat.h5', "r")  # 加载测试数据test_set_x_orig = np.array(test_dataset["test_set_x"][:])test_set_y_orig = np.array(test_dataset["test_set_y"][:])classes = np.array(test_dataset["list_classes"][:])  # 加载标签类别数据，这里的类别只有两种，1代表有猫，0代表无猫train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))  # 把数组的维度从(209,)变成(1, 209)，这样好方便后面进行计算[1 1 0 1] -> [[1][1][0][1]]test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))  # 从(50,)变成(1, 50)return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classesdef sigmoid(Z):A = 1 / (1 + np.exp(-Z))return Adef relu(Z):A = np.maximum(0, Z)assert (A.shape == Z.shape)return Adef initialize_parameters_deep(layers_dims):""":param layers_dims: list of neuron numexample: layer_dims=[5,4,3]，表示输入层有5个神经元，第一层有4个，最后二层有3个神经元（还有输出层的1个神经元）:return: parameters: the w,b of each layer"""np.random.seed(1)parameters = {}L = len(layers_dims)for l in range(1, L):parameters[f"W{l}"] = np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1])parameters[f"b{l}"] = np.zeros((layers_dims[l], 1))assert (parameters[f"W{l}"].shape == (layers_dims[l], layers_dims[l - 1]))assert (parameters[f"b{l}"].shape == (layers_dims[l], 1))return parameters  # W1,b1,W2,b2def linear_forward(A, W, b):"""线性前向传播"""Z = np.dot(W, A) + bassert (Z.shape == (W.shape[0], A.shape[1]))return Zdef linear_activation_forward(A_prev, W, b, activation):""":param A_prev: 上一层得到的A，输入到本层来计算本层的Z和A，第一层时A_prev就是输入X:param W:本层的w:param b:本层的b:param activation: 激活函数"""Z = linear_forward(A_prev, W, b)if activation == "sigmoid":A = sigmoid(Z)elif activation == "relu":A = relu(Z)else:assert (1 != 1), "there is no support activation!"assert (A.shape == (W.shape[0], A_prev.shape[1]))linear_cache = (A_prev, W, b)cache = (linear_cache, Z)return A, cachedef L_model_forward(X, parameters):"""前向传播:param X: 输入特征:param parameters: 每一层的初始化w,b"""caches = []A = XL = len(parameters) // 2  # W1,b1,W2,b2, L=2for l in range(1, L):A_prev = AA, cache = linear_activation_forward(A_prev, parameters[f"W{l}"], parameters[f"b{l}"], 'relu')caches.append(cache)  # A1,(X,W1,b1,Z1)AL, cache = linear_activation_forward(A, parameters[f"W{L}"], parameters[f"b{L}"], activation="sigmoid")caches.append(cache)  # A2,(A1,W2,b2,Z2)assert (AL.shape == (1, X.shape[1]))return AL, cachesdef compute_cost(AL, Y):m = Y.shape[1]logprobs = np.multiply(Y, np.log(AL)) + np.multiply((1 - Y), np.log(1 - AL))cost = (-1 / m) * np.sum(logprobs)assert (cost.shape == ())return costdef linear_backward(dZ, cache):""":param dZ: 后面一层的dZ:param cache: 前向传播保存下来的本层的变量:return 本层的dw、db，前一层da"""A_prew, W, b = cachem = A_prew.shape[1]dW = np.dot(dZ, A_prew.T) / mdb = np.sum(dZ, axis=1, keepdims=True) / mdA_prev = np.dot(W.T, dZ)assert (dA_prev.shape == A_prew.shape)assert (dW.shape == W.shape)assert (db.shape == b.shape)return dA_prev, dW, dbdef linear_activation_backward(dA, cache, activation):""":param dA: 本层的dA:param cache: 前向传播保存的本层的变量:param activation: 激活函数:"sigmoid"或"relu":return 本层的dw、db，前一次的dA"""linear_cache, Z = cache# 首先计算本层的dZif activation == 'relu':dZ = 1 * dAdZ[Z <= 0] = 0elif activation == 'sigmoid':A = sigmoid(Z)dZ = dA * A * (1 - A)else:assert (1 != 1), "there is no support activation!"assert (dZ.shape == Z.shape)# 这里我们又顺带根据本层的dZ算出本层的dW和db以及前一层的dAdA_prev, dW, db = linear_backward(dZ, linear_cache)return dA_prev, dW, dbdef L_model_backward(AL, Y, caches):""":param AL: 最后一层A:param Y: 真实标签:param caches: 前向传播的保存的每一层的相关变量  (A_prev, W, b)，Z"""grads = {}L = len(caches)  # 2Y = Y.reshape(AL.shape)  # 让真实标签与预测标签的维度一致dAL = -np.divide(Y, AL) + np.divide(1 - Y, 1 - AL)  # dA2# 计算最后一层的dW和db，由成本函数来计算current_cache = caches[-1]  # 1,2grads[f"dA{L - 1}"], grads[f"dW{L}"], grads[f"db{L}"] = linear_activation_backward(dAL, current_cache,"sigmoid")  # dA1, dW2, db2# 计算前L-1层的dw和db，因为最后一层用的是sigmoid，for c in reversed(range(1, L)):  # reversed(range(1,L))的结果是L-1,L-2...1。是不包括L的。第0层是输入层，不必计算。 caches[0,1] L = 2  1,1# c表示当前层grads[f"dA{c - 1}"], grads[f"dW{c}"], grads[f"db{c}"] = linear_activation_backward(grads[f"dA{c}"],caches[c - 1],"relu")return gradsdef update_parameters(parameters, grads, learning_rate):L = len(parameters) // 2for l in range(1, L + 1):parameters[f"W{l}"] = parameters[f"W{l}"] - grads[f"dW{l}"] * learning_rateparameters[f"b{l}"] = parameters[f"b{l}"] - grads[f"db{l}"] * learning_ratereturn parametersdef dnn_model(X, Y, layers_dim, learning_rate=0.0075, num_iterations=3000, print_cost=False):np.random.seed(1)costs = []parameters = initialize_parameters_deep(layers_dim)for i in range(0, num_iterations):AL, caches = L_model_forward(X, parameters)cost = compute_cost(AL, Y)grads = L_model_backward(AL, Y, caches)parameters = update_parameters(parameters, grads, learning_rate)if print_cost and i % 100 == 0:print("训练%i次后成本是: %f" % (i, cost))costs.append(cost)# 画出成本曲线图plt.plot(np.squeeze(costs))plt.ylabel('cost')plt.xlabel('iterations (per tens)')plt.title("Learning rate =" + str(learning_rate))plt.show()return parametersdef predict(X, parameters):m = X.shape[1]n = len(parameters) // 2p = np.zeros((1, m))probas, caches = L_model_forward(X, parameters)# 将预测结果转化成0和1的形式，即大于0.5的就是1，否则就是0for i in range(0, probas.shape[1]):if probas[0, i] > 0.5:p[0, i] = 1else:p[0, i] = 0return pif __name__ == "__main__":train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()# 我们要清楚变量的维度，否则后面会出很多问题。下面我把他们的维度打印出来。train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).Ttest_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).Tprint("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))print("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))train_set_x = train_set_x_flatten / 255test_set_x = test_set_x_flatten / 255layers_dims = [12288, 20, 7, 5, 1]# 根据上面的层次信息来构建一个深度神经网络，并且用之前加载的数据集来训练这个神经网络，得出训练后的参数parameters = dnn_model(train_set_x, train_set_y, layers_dims, num_iterations=2000, print_cost=True)# 对训练数据集进行预测pred_train = predict(train_set_x, parameters)print("预测准确率是: " + str(np.sum((pred_train == train_set_y) / train_set_x.shape[1])))# 对测试数据集进行预测pred_test = predict(test_set_x, parameters)print("预测准确率是: " + str(np.sum((pred_test == test_set_y) / test_set_x.shape[1])))