机器学习课程学习周报五
文章目录
- 机器学习课程学习周报五
- 摘要
- Abstract
- 一、机器学习部分
- 1.1 向量序列作为模型输入
- 1.1.1 文字的向量表达
- 1.1.2 语音的向量表达
- 1.2 自注意力机制原理
- 1.2.1 自注意力机制理论
- 1.2.2 矩阵运算自注意力机制
- 1.3 多头自注意力
- 1.4 位置编码
- 1.5 截断自注意力
- 1.6 自注意力与卷积神经网络
- 1.7 自注意力与循环神经网络
- 总结
摘要
在本周的学习中,我深入研究了机器学习模型中的向量序列输入和自注意力机制。首先,我探讨了文字和语音的向量表达方法,了解了one-hot编码和词嵌入在文字处理中的应用,以及窗口和帧移在语音处理中的概念。接着,我详细分析了自注意力机制的理论和运作过程,包括点积和相加两种计算关联性的方法,以及查询-键-值模式的应用。此外,我学习了矩阵运算中如何实现自注意力机制,并进一步研究了多头自注意力的原理和优势。最后,我简要介绍了位置编码在自注意力层中的作用。
Abstract
In this week’s studies, I delved into vector sequence inputs and self-attention mechanisms in machine learning models. Firstly, I explored the vector representation methods for text and speech, understanding the applications of one-hot encoding and word embeddings in text processing, as well as the concepts of window and frame shift in speech processing. Next, I conducted a thorough analysis of the theory and operation of self-attention mechanisms, including dot product and additive methods for calculating relevance, and the Query-Key-Value (QKV) model. Additionally, I learned how to implement self-attention mechanisms using matrix operations and further studied the principles and advantages of multi-head self-attention. Finally, I briefly introduced the role of positional encoding in self-attention layers.
一、机器学习部分
1.1 向量序列作为模型输入
举两个例子来说明输入是向量序列的情况:
1.1.1 文字的向量表达
当网络的输入是一个句子时,把一个句子里面的每一个词汇都描述成一个向量,用向量来表示,模型的输入就是一个向量序列,而该向量序列的大小每次都不一样(句子的长度不一样,向量序列的大小就不一样)。

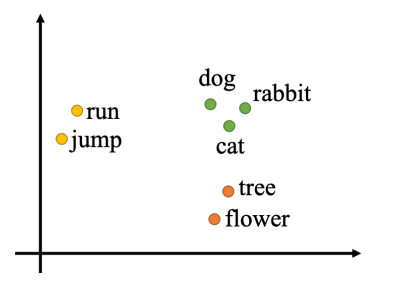
将词汇表示成向量最简单的做法是one-hot编码,创建一个很长的向量,该向量的长度跟世界上存在的词汇的数量是一样多的,但这个方法没有考虑词汇彼此之间的关系。因此更常用的是词嵌入(word embedding),词嵌入会给每一个词汇一个向量,而这个向量是包含语义信息的,相同类别的词向量能聚集在一起。
1.1.2 语音的向量表达
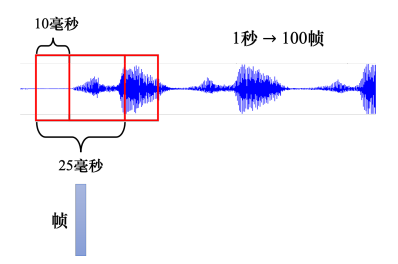
把一段声音信号取一个范围,这个范围叫做一个窗口(window),窗口的长度一般为25毫秒,把该窗口里面的信息描述成一个向量,这个向量称为一帧(frame)。而窗口的每次移动10毫秒,这被称为帧移(frame shift),这意味着每次窗口移动10毫秒然后重新取一个25毫秒长的新窗口,因此1秒钟包含 1000 ( 1 秒) / 10 ( 10 毫秒) = 100 (个向量) 1000(1秒)/10(10毫秒) = 100(个向量) 1000(1秒)/10(10毫秒)=100(个向量)。

这一章主要讨论模型输入与输出相同的情况,模型的输入是一组的向量,它可以是文字,可以是语音,可以是图,而模型的输出是每一个输入向量都有一个对应的标签,如果是回归问题,每个标签是一个数值。如果是分类问题, 每个标签是一个类别。模型的输出还有两种其它情况,分别是输入是一个序列输出是一个标签和序列输入到序列输出问题,这两种情况不在这里讨论。
1.2 自注意力机制原理
1.2.1 自注意力机制理论
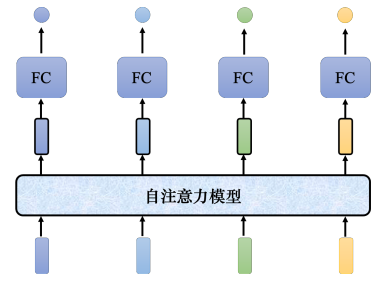
自注意力模型会输入整个序列的数据,输入几个向量,它就输出几个向量。上图中输入4个向量,它就输出4个向量。而这4个向量都是考虑整个序列以后才得到的,所以输出的向量有一个黑色的框,代表它不是一个普通的向量,它是考虑了整个句子以后才得到的信息。接着再把考虑整个句子的向量丢进全连接网络,再得到输出。因此全连接网络不是只考虑一个非常小的范围或一个小的窗口,而是考虑整个序列的信息,再来决定现在应该要输出什么样标签。全连接网络和自注意力模型可以交替使用,全连接网络专注于处理某一个位置的信息,自注意力把整个序列信息再处理一次。
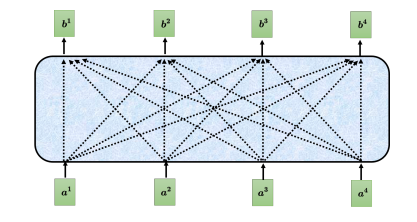
自注意力模型的运作过程是,先输入一串的向量,这个向量可能是整个网络的输入,也可能是某个隐藏层的输出,所以不用 x x x来表示它,而用 a a a来表示它。自注意力要输出一组 向量 b b b,每个 b b b都是考虑了所有的 a a a后才生成出来的。 b 1 {b^1} b1、 b 2 {b^2} b2、 b 3 {b^3} b3、 b 4 {b^4} b4是考虑整个输入的 序列 a 1 {a^1} a1、 a 2 {a^2} a2、 a 3 {a^3} a3、 a 4 {a^4} a4才产生出来的。
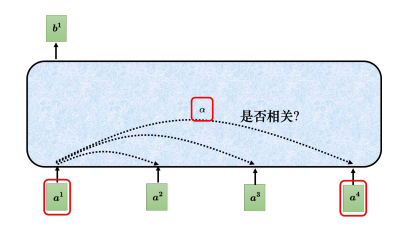
以计算 b 1 {b^1} b1为例,第一个步骤是根据 a 1 {a^1} a1找出输入序列里面跟 a 1 {a^1} a1相关的其他向量。使用一个计算注意力的模块计算两个向量之间的关联性,一般的做法是点积(dot product),把输入的两个向量分别乘上两个不同的矩阵,左边这个向量乘上矩阵 W q {W^q} Wq,右边这个向量乘上矩阵 W k {W^k} Wk,得到两个向量 q q q跟 k k k,再把 q q q跟 k k k做点积,得到关联性结果 α {\alpha} α。
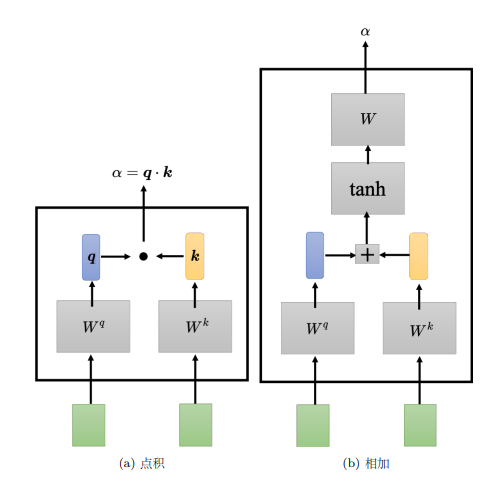
还有另一种计算关联性的方法是相加(additive), q q q和 k k k不是做点积,而是相加之后放入tanh函数中,再乘上矩阵 W {W} W得到 α {\alpha} α。而自注意力模型一般采用查询-键-值(Query-Key-Value,QKV)模式。 分别计算 a 1 {a^1} a1与 a 2 {a^2} a2、 a 3 {a^3} a3、 a 4 {a^4} a4之间的关联性,具体做法为把 a 1 {a^1} a1乘上 W q {W^q} Wq得到 q 1 {q^1} q1, q {q} q称为查询(query)。接下来要把 a 2 {a^2} a2、 a 3 {a^3} a3、 a 4 {a^4} a4和 a 1 {a^1} a1(在实践中 a 1 {a^1} a1也会和自己算关联性)乘上 W k {W^k} Wk得到向量 k k k,向量 k k k称为键(key),然后将 q 1 {q^1} q1与4个 k k k分别做内积得到4个关联性 α {\alpha} α,关联性 α {\alpha} α也被称为注意力的分数。
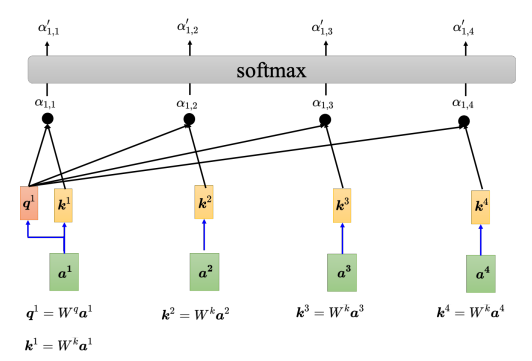
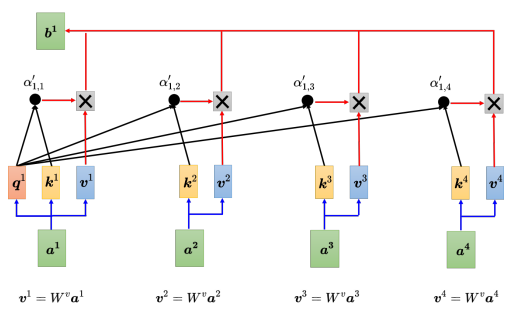
接着,对所有的注意力分数做一个softmax操作,将注意力分数 α {\alpha} α归一化得到 α ′ \alpha ' α′。得到 α ′ \alpha ' α′以后,接下来根据 α ′ \alpha ' α′去抽取出序列里面重要的信息。把向量 a 1 {a^1} a1到 a 4 {a^4} a4乘上 W v {W^v} Wv得到新的向量: v 1 {v^1} v1、 v 2 {v^2} v2、 v 3 {v^3} v3、 v 4 {v^4} v4,接下来把每一个向量都去乘上注意力的分数 α ′ \alpha ' α′,再把它们加起来:
b 1 = ∑ i α ′ 1 , i v i {b^1} = \sum\limits_i^{} {{{\alpha '}_{1,i}}{v^i}} b1=i∑α′1,ivi
如果 a 1 {a^1} a1跟 a 2 {a^2} a2的关联性很强,即 α ′ 1 , 2 {{{\alpha '}_{1,2}}} α′1,2的值很大。在做加权和(weighted sum)以后,得到的 b 1 {b^1} b1的值就可能会比较接近 v 2 {v^2} v2,所以谁的注意力的分数最大,谁的 v v v就会主导(dominant) 抽出来的结果。以上讲述了如何从一整个序列得到 b 1 {b^1} b1。同理,可以计算出 b 2 {b^2} b2到 b 4 {b^4} b4。
1.2.2 矩阵运算自注意力机制
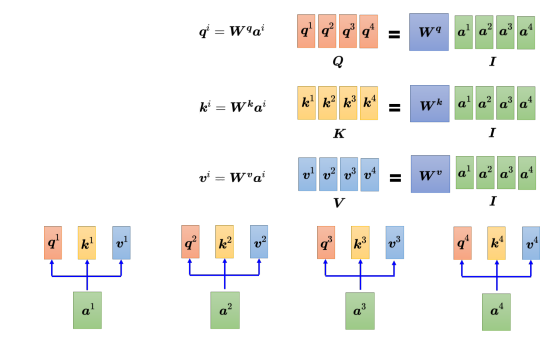
现在已经知道 a 1 {a^1} a1到 a 4 {a^4} a4,每一个 a a a都要分别产生 q q q、 k k k 和 v v v。如果用矩阵运算表达这个操作,每个 a i {a^i} ai都乘上一个矩阵 W q {W^q} Wq得到 q i {q^i} qi,这些不同的 a a a和 q q q可以分别合起来当作矩阵, I I I乘上 W q {W^q} Wq得到 Q Q Q。而产生 k k k和 v v v的操作跟 q q q是一模一样的,把 I I I乘上矩阵 W k {W^k} Wk, 就得到矩阵 K K K;把 I I I乘上矩阵 W v {W^v} Wv, 就得到矩阵 V V V。
紧接着需要计算注意力分数,把 q 1 {q^1} q1和 k 1 {k^1} k1做内积(inner product),也是点乘,得到 α 1 , 1 {\alpha _{1,1}} α1,1,接着用 q 1 {q^1} q1和 k 2 {k^2} k2做内积,以此类推。这个操作可以看成是矩阵和向量相乘,把 ( k 1 ) T {({k^1})^{\rm T}} (k1)T到 ( k 4 ) T {({k^4})^{\rm T}} (k4)T拼起来当作是一个矩阵的四行,再把这个矩阵乘上 q 1 {q^1} q1,可得到注意力分数矩阵,该矩阵的每一行都是注意力分数。
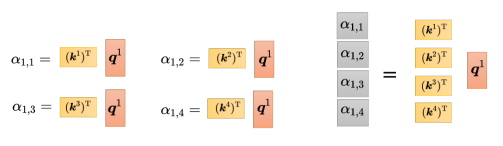
现在不仅是 q 1 {q^1} q1, q 2 {q^2} q2到 q 4 {q^4} q4都需要计算注意力分数。利用矩阵运算的方法是,一个矩阵的行都是 k k k,即 k 1 {k^1} k1到 k 4 {k^4} k4,另一个矩阵的列就是 q q q,从 q 1 {q^1} q1到 q 4 {q^4} q4,如下图所示两个矩阵相乘即可得到整体的注意力分数矩阵。

最后需要计算自注意力模块的输出 b b b,在上图中 A A A通过softmax归一化得到了 A ′ A' A′,需要把 v 1 {v^1} v1到 v 4 {v^4} v4乘上对应的 α {\alpha} α再相加得到 b b b。在矩阵运算中,把 v 1 {v^1} v1到 v 4 {v^4} v4当成是矩阵 V V V的 4 个列拼起来,把 A ′ A' A′的第一个列乘上 V V V就得到 b 1 {b^1} b1,把 A ′ A' A′的第二个列乘上 V V V得到 b 2 {b^2} b2,以此类推,等于把矩阵 A ′ A' A′乘上矩阵 V V V得到矩阵 O O O。
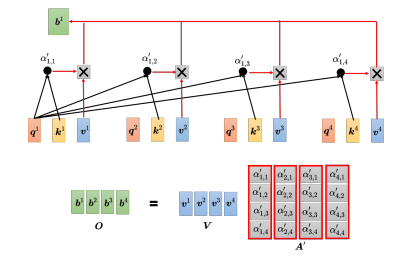
其中 A ′ A' A′称为注意力矩阵(attention matrix),而自注意力层里面唯一需要学习的参数就只有 W q {W^q} Wq、 W k {W^k} Wk和 W v {W^v} Wv,需要通过训练数据把它学习出来,其他操作都没有未知的参数,都是人为设定好的。
1.3 多头自注意力
多头自注意力(multi-head self-attention)是自注意力的进阶版本,多头注意力在某些任务上的表现更佳,但多头的数量是个超参数。具体来说,在自注意力机制中,计算相关性是用 q q q去找相关的 k k k,但相关性有很多种不同的形式,所以也许可以有多个 q q q,不同的 q q q负责不同种类的相关性,这就是多头注意力。
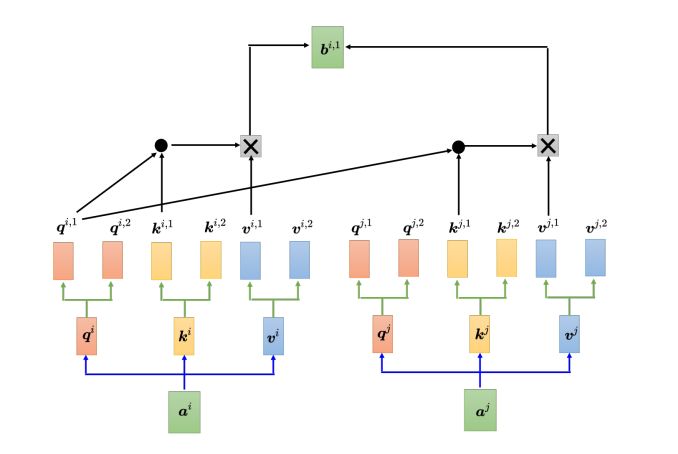
以两头的自注意力模型为例,先把 a i a^i ai分别乘上两个矩阵,得到 q i , 1 {q^{i,1}} qi,1 和 和 和 q i , 2 {q^{i,2}} qi,2,同样地也会对应得到两个 k k k和两个 v v v,而对其他位置 a j a^j aj等,同样地也会产生两个 q q q、两个 k k k和两个 v v v。而在计算注意力矩阵时,每个头只计算自己的注意力分数,也就是上图中 q i , 1 {q^{i,1}} qi,1分别与 k i , 1 {k^{i,1}} ki,1、 k j , 1 {k^{j,1}} kj,1算注意力。做加权和时,把注意力的分数分别乘 v i , 1 {v^{i,1}} vi,1和 v j , 1 {v^{j,1}} vj,1,再相加得到 b i , 1 {b^{i,1}} bi,1,这里只用了其中的一个头。另一个头的计算方式如下:
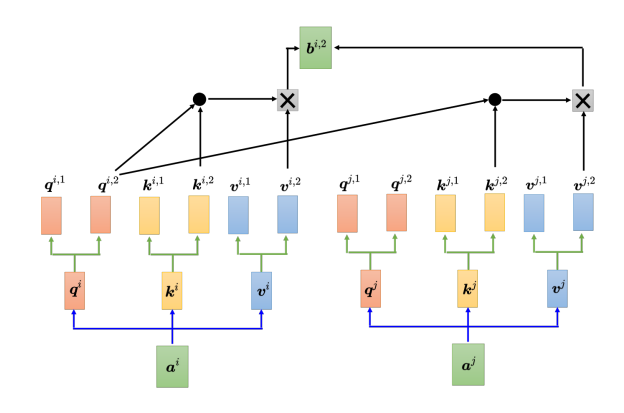
1.4 位置编码
对于自注意力层,输入的向量有位置1、2、3、4等等,但是这个位置顺序没有任何差别,因为自注意力层对这几个位置的操作是一模一样的。此时,位置的信息被忽略了,在如词性标注的任务中,词汇的位置信息就显得尤为重要,在需要考虑位置信息时,就要用到位置编码(positional encoding)。位置编码为每一个位置设定一个向量,即位置向量(positional vector)。位置向量用 e i {e^i} ei 来表示,上标 来表示,上标 来表示,上标 i i i表示位置,将 e i {e^i} ei加入到 a i {a^i} ai中,其就包含了位置信息。
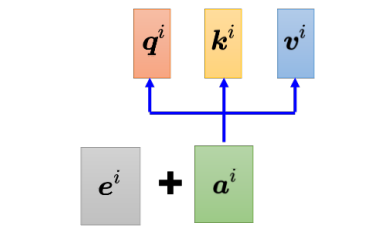
最早的位置编码是用正弦函数所产生的,在“Attention Is All You Need” 论文中,其位置向量是通过正弦函数和余弦函数所产生的。
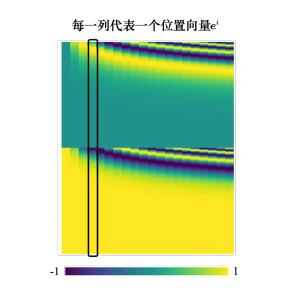
1.5 截断自注意力
在自注意力应用于语音处理中,语音的向量序列较长在计算注意力矩阵的时候,其复杂度是其长度的平方,假设矩阵的长度为 L L L,计算注意力矩阵 A ′ A' A′需要做 L 2 {L^2} L2次的内积,因此在序列较长是,计算量较大。
截断自注意力(truncated self-attention)可以处理向量序列长度过大的问题。截断自注意力在做自注意力的时候不要看一整句话,就只看一个小的范围就好,这个范围是人设定的。在做语音识别的时候,如果要辨识某个位置有什么样的音标,这个位置有什么样的内容,并不需要看整句话,只要看这句话以及它前后一定范围之内的信息,就可以判断。
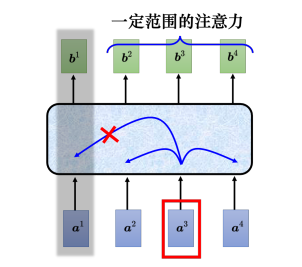
1.6 自注意力与卷积神经网络
自注意力还可以被用在图像上。一张图像可以看作是一个向量序列,一张分辨 率为 5 × 10 的图像可以表示为一个大小为 5 × 10 × 3 的张量,每一个位置的像素可看作是一个三维的向量,整张图像是 5 × 10 个向量。
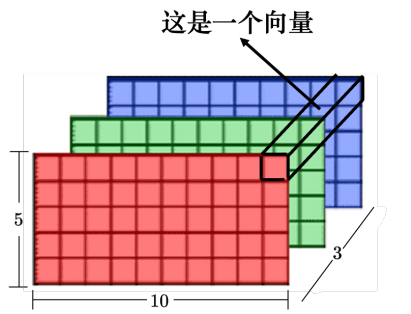
用自注 意力来处理一张图像,假设红色框内的“1”是要考虑的像素,它会产生查询,其他像素产生键。在做内积的时候,考虑的不是一个小的范围,而是整张图像的信息。
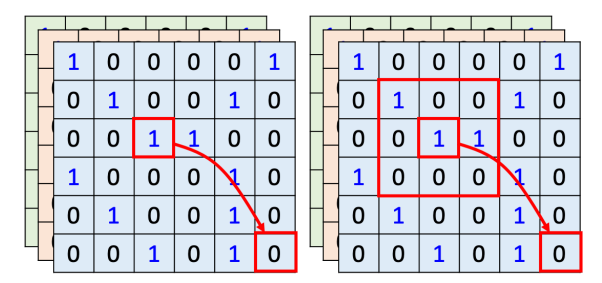
在做卷积神经网络的时候,卷积神经网络会“画”出一个感受野,每一个滤波器,每一个神经元,只考虑感受野范围里面的信息。所以如果我们比较卷积神经网络跟自注意力会发现,卷积神经网络可以看作是一种简化版的自注意力,因为在做卷积神经网络的时候,只考虑感受野里面 的信息。而在做自注意力的时候,会考虑整张图像的信息。在卷积神经网络里面,我们要划定感受野。每一个神经元只考虑感受野里面的信息,而感受野的大小是人决定的。而用自注意力去找出相关的像素,就好像是感受野是自动被学出来的,网络自己决定感受野的形状。

自注意力只要设定合适的参数,就可以做到跟卷积神经网络一模一样的事情,所以自注意力是更 灵活的卷积神经网络,而卷积神经网络是受限制的自注意力。
1.7 自注意力与循环神经网络
自注意力跟循环神经网络有一个显而易见的不同,自注意力的每一个向量都考虑了整个输 入的序列,而循环神经网络的每一个向量只考虑了左边已经输入的向量,它没有考虑右边的向量。但循环神经网络也可以是双向的,所以如果用双向循环神经网络(Bidirectional Recurrent Neural Network,Bi-RNN),那么每一个隐状态的输出也可以看作是考虑了整个输入的序列。
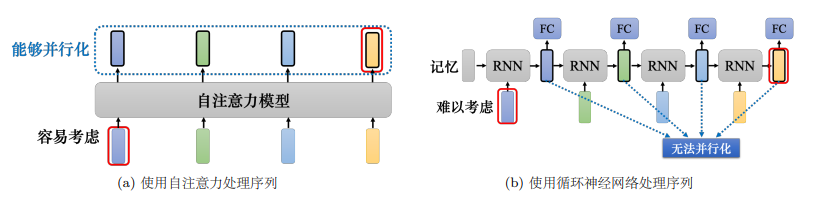
但是假设把循环神经网络的输出跟自注意力的输出拿来做对比,就算使用双向循环神经网络还是有一些差别的。如上图所示,对于循环神经网络,如果最右边黄色的向量要考虑最左边的输入,它就必须把最左边的输入存在记忆里面,才能不“忘掉”,一路带到最右边,才能够在最后一个时间点被考虑。但自注意力输出一个查询,输出一个键,只要它们匹配 (match)得起来,“天涯若比邻”,自注意力可以轻易地从整个序列上非常远的向量抽取信息。
另外一个更主要的不同是,循环神经网络在处理输入、输出均为一组序列的时候,是没有办法并行化的。比如计算第二个输出的向量,不仅需要第二个输入的向量,还需要前一个时间点的输出向量,但自注意力可以。因此,自注意力会比循环神经网络更有效率。很多的应用已经把循环神经网络的架构逐渐改成自注意力的架构了。
总结
尽管循环神经网络在某种程度上已经过时,并且被自注意力模型所代替,但从基础学习的角度仍应该搞明白循环神经网络的原理,因此会在下一周开启这一部分的学习。






![[微信小程序] css 解决纯数字或字母不自动换行的问题、控制文字行数](https://i-blog.csdnimg.cn/direct/eacd79d536f247fbb081399a8f9e8248.png)