MATLAB计算心理声学烦恼度例子

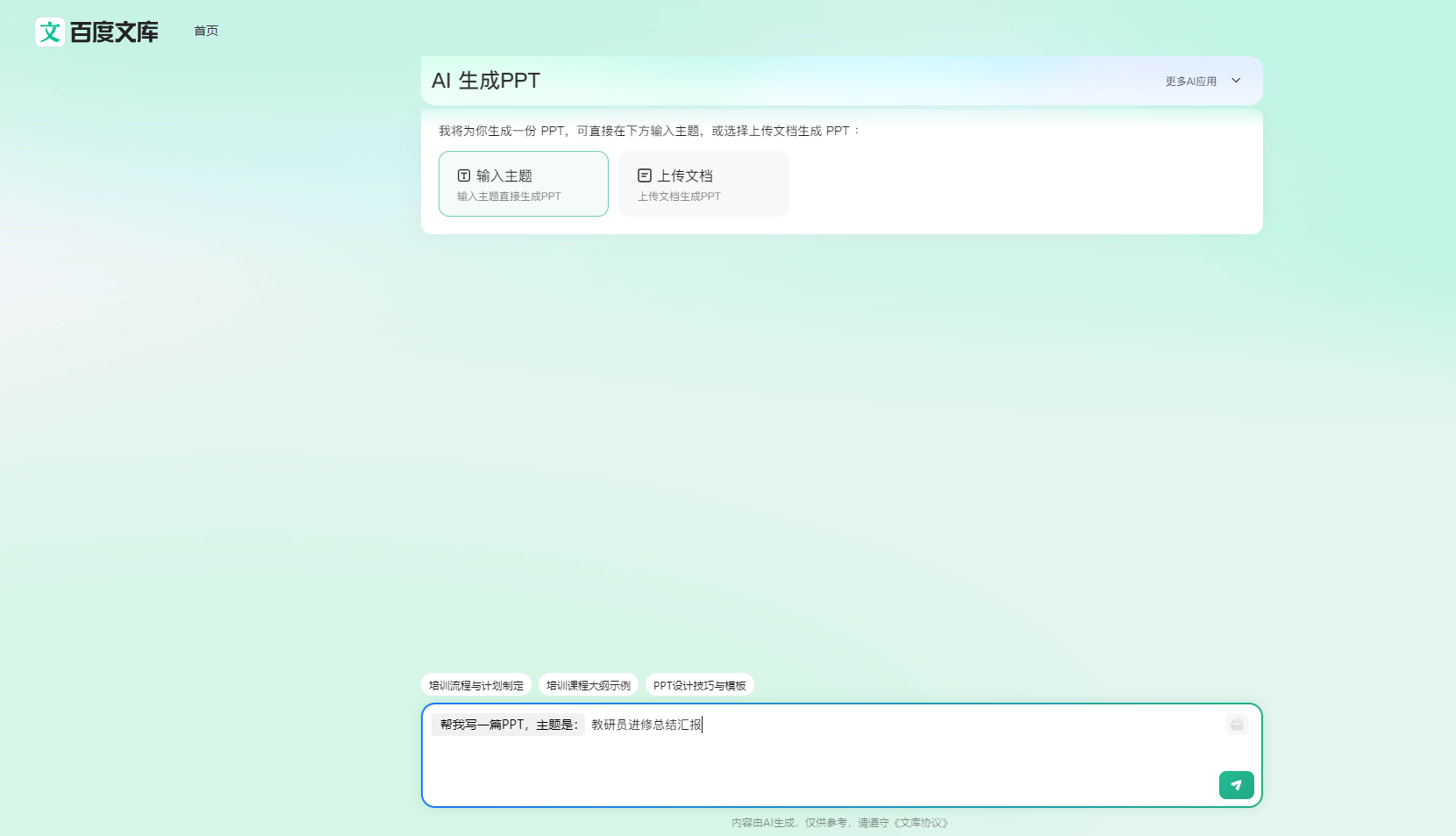
在这个例子中，您测量发动机噪音，并使用心理声学指标来模拟其感知响度、尖锐度、波动强度、粗糙度和总体烦扰程度。然后，模拟添加隔音材料，重新计算总体噪音水平。最后，比较恼人程度，并显示应用隔音材料后的感知改善效果。

记录电平校准

心理声学测量使用校准过的麦克风输入电平能产生最准确的结果。要使用校准麦克风将录音电平与声压级计的读数相匹配，可以使用 1 kHz 音源（如在线音源或手机应用程序）和校准的声压级计。1 kHz 校准音的声压级应足够响亮，足以盖过任何背景噪声。有关使用 MATLAB 作为 1 kHz 音源的校准示例，请参阅校准麦克风。

模拟音调录音并加入一些背景噪音。假设声压计读数为 83.1 dB（C 加权）。

FS = 48e3;
t = (1:2*FS)/FS;
s = rng("default");
testTone = 0.46*sin(2*pi*t*1000).' + .1*pinknoise(2*FS);
rng(s)
splMeterReading = 83.1;

要计算录音链的校准电平，请调用 calibrateMicrophone 并指定测试音、采样率、声压级读数和声压级计的频率加权。为了补偿可能的背景噪声并产生精确的校准电平，请匹配声压级计的频率加权设置。

calib = calibrateMicrophone(testTone,FS,splMeterReading,FrequencyWeighting="C-weighting");

声压级 (SPL)

有了录音链的校准因子后，就可以进行声学测量了。使用物理测量仪时，您只能使用测量时选择的设置。使用 splMeter 对象，您可以在录音完成后更改设置。这样就可以轻松尝试不同的时间和频率加权选项。

加载引擎记录并创建相应的时间矢量。

[x,FS] = audioread("Engine-16-44p1-stereo-20sec.wav");
x = x(1:8*FS,1); % use only channel 1 and keep only 8 seconds.
t = (1:size(x,1))/FS;

创建一个 splMeter 对象，选择 C 计权、快速时间计权和 0.2 秒间隔峰值声压级测量。

spl = splMeter(CalibrationFactor=calib, ...FrequencyWeighting="C-weighting", ...TimeWeighting="Fast", ...TimeInterval=0.2, ...SampleRate=FS);

绘制声压级和峰值声压级图。

[LCF,~,LCpeak] = spl(x);
plot(t,LCpeak,t,LCF)
legend("LCpeak","LCF",Location="southeast")
title("SPL Measurement of Engine Noise")
xlabel("Time (seconds)")
ylabel("SPL (dB)")
ylim([70 95])
grid on

心理声学指标

响度级别

监测声压级对于遵守职业安全规定非常重要。声压级测量的是听力正常（无听力障碍）的人所感知的响度。声学响度功能还能显示哪些频段对响度的感知贡献最大。

使用与之前相同的校准电平，并假设是自由声场录音（默认值），绘制静态响度图。

acousticLoudness(x,FS,calib)

响度为 23.8 sone，大部分噪音低于 3.3（bark）。使用 bark2hz 将 3.3 Bark 转换为 Hz

fprintf("Loudness frequency of 3.3 Bark: %d Hz\n",round(bark2hz(3.3),-1));

3.3 Bark 的响度频率：330 赫兹

acousticLoudness 函数以音调为单位返回感知响度。要理解音调测量值，可将其与声压级（dB）读数进行比较。响度为 60 音的信号被认为与以 60 dB SPL 测量的 1 kHz 音一样响亮。使用 sone2phon 将 23.8 sones 转换为 phons 表明，发动机噪音的响度感知与在 86 dB SPL 下测量的 1 kHz 音调一样响亮。

fprintf("Equivalent 1 kHz SPL: %d phons\n",round(sone2phon(23.8)));

等效 1 kHz 声压级：86 phons

在对数刻度上用单位phons和频率Hz绘制自己的曲线图。

[sone,spec] = acousticLoudness(x,FS,calib);
barks = 0.1:0.1:24; % Bark scale for ISO 532-1 loudness
hz = bark2hz(barks);
specPhon = sone2phon(spec);
semilogx(hz,specPhon)
title("Specific Loudness")
subtitle(sprintf("Loudness = %.1f phons",sone2phon(sone)))
xlabel("Frequency (Hz)")
ylabel("Loudness (phons/Bark)")
xlim(hz([1,end]))
grid on

您还可以绘制随时间变化的响度和特定响度，以分析发动机声音是否随时间变化。这可以与其他相关的时变数据一起显示，例如发动机每分钟转速 (RPM)。在这种情况下，噪声是静止的，但您可以观察到噪声的脉冲性质。

acousticLoudness(x,FS,calib,TimeVarying=true,TimeResolution="high")

绘制特定响度与频率（赫兹）的关系图（对数刻度）。

[tvsoneHD,tvspecHD,perc] = acousticLoudness(x,FS,calib,TimeVarying=true,TimeResolution="high");
tvspec = tvspecHD(1:4:end,:,:); % for standard resolution measurements
spectimeHD = 0:5e-4:5e-4*(size(tvspecHD,1)-1); % time axis for loudness output
clf; % do not reuse the previous subplot
surf(spectimeHD,hz,sone2phon(tvspecHD).',EdgeColor="interp");
set(gca,View=[0 90],YScale="log",YLim=hz([1,end]));
title("Specific Loudness (HD)")
zlabel("Specific Loudness (phons/Bark)")
ylabel("Frequency (Hz)")
xlabel("Time (seconds)")
colorbar

尖锐度级别

声音的尖锐感会极大地影响声音的整体烦扰程度。使用 acousticSharpness 函数可以估算出声音信号的尖锐程度。

sharp = acousticSharpness(spec)

sharp = 1.1512

粉红噪声的尖锐度为 2 acums。这意味着发动机噪音偏向低频。

绘制随时间变化的尖锐度。

acousticSharpness(x,FS,calib,TimeVarying=true);

波动度

在发动机噪音的情况下，低频调制会导致感知到的恼人程度。首先，查看信号中存在哪些调制频率。

N = 2^nextpow2(size(x,1));
xa = abs(x); % Use the rectified signal
pspectrum(xa-mean(xa),FS,FrequencyLimits=[0 80],FrequencyResolution=1)
title("Modulation Frequencies")

调制频率的峰值为 24.9 赫兹。低于 30 赫兹时，调制主要表现为波动。在 49.7 赫兹处有第二个峰值，处于粗糙度范围内。

使用 acousticFluctuation 计算可感知的波动强度。在这段录音中，发动机噪音相对恒定，因此我们让算法自动检测最易听到的波动频率 (fMod)。

acousticFluctuation(x,FS,calib)

用赫兹而不是bark来解释结果。为减少计算量，可重复使用之前计算的随时间变化的特定响度。或者，您也可以指定您感兴趣的调制频率。

[vacil,spec,fMod] = acousticFluctuation(tvspec,ModulationFrequency=24.9);
clf; % do not reuse previous subplot
flucHz = bark2hz(0.5:0.5:23.5);
spectime = 0:2e-3:2e-3*(size(spec,1)-1);
surf(spectime,flucHz,spec.',EdgeColor="interp");
set(gca,View=[0 90],YScale="log",YLim=flucHz([1,end]));
title("Specific Fluctuation Strength")
zlabel("Specific Fluctuation Strength (vacils/Bark)")
ylabel("Frequency (Hz)")
xlabel("Time (seconds)")
colorbar

Roughness

使用 acousticRoughness 函数计算信号的可感知粗糙度。让算法自动检测最易听到的调制频率 (fMod)。

acousticRoughness(x,FS,calib)

用赫兹而不是bark来解释结果。为减少计算量，可重复使用之前计算的随时间变化的特定响度。指定调制频率。

[asper,specR,fModR] = acousticRoughness(tvspecHD,ModulationFrequency=49.7);
clf; % do not reuse previous subplot
rougHz = bark2hz(0.5:0.5:23.5);
surf(spectimeHD,rougHz,specR.',EdgeColor="interp");
set(gca,View=[0 90],YScale="log",YLim=rougHz([1,end]));
title("Specific Roughness")
zlabel("Specific Roughness (aspers/Bark)")
ylabel("Frequency (Hz)")
xlabel("Time (seconds)")
colorbar

音调

发动机噪声的另一个可感知属性是音调，包括音调与其他噪声之间的比率。绘制信号的音调噪声比，其中包括带有突出指示器等信息的数据点。音调指标不需要校准因子。

acousticToneToNoiseRatio(x,FS)

此外，还显示随时间变化的突出比。点击曲线图可获得该时间和频率的详细信息。

acousticProminenceRatio(x,FS,TimeVarying=true)

sound quality

对于整体音质评价，将前面的指标结合起来，就能得出心理声学烦扰指标。其关系如下：

$PA=N(1+\sqrt{|g1(S)|^2+|g2(F,R)|^2})$

利用心理声学实验的结果进行了量化描述：

$PA=N_{5}(1+\sqrt{\omega _{S}^2+\omega _{FR}^2})$

N 5 :百分位数响度（仅有 5%的时间超过该水平）

$\omega _{S}=(S-1.75)*(0.25*log_{10}(N_{5}+10))$

其中S>1.75，S 为尖锐度，单位为 acum

$\omega _{FR}=\frac{2.18}{N_{5}^{0.4}}(0.4*F+0.6*R)$

其中，F 是以 vacil 为单位的波动强度，R 是以 asper 为单位的粗糙度

在本例中，尖锐度小于 1.75，因此不是影响因素，因此可以将 $\omega _{S}$ 设置为零

当 TimeVarying（时间变化）设置为 true 时，acousticLoudness（声学响度）的第三个输出将返回第二个值 N5。

N5 = perc(2);

计算忽略信号第一秒的平均波动强度。

f = mean(vacil(501:end,1));

计算忽略第一秒信号的平均粗糙度。

r = mean(asper(2001:end,1));

计算 Zwicker 的心理声学烦扰度量。

pa = N5 * (1 + abs(2.18/(N5^.4)*(.4*f+.6*r)))

pa = 26.3402

对于飞机或发动机等带有音调成分的噪声，S. R. More 对这一指标进行了改进，将音调也包括在内：

$PAT=N_{5}*(1+\sqrt{\gamma_{0}+\gamma_{1}\omega _{S}^{2}+\gamma_{2}\omega _{FR}^{2}+\gamma_{3}\omega _{T}^{2}})$

其中：

$\omega_{T}^{2}=(1-e^{\gamma_{4}N_{5}})*(1-e^{\gamma_{5}K_{5}})$

$\gamma_{0}=-0.16,\gamma_{1}=11.48,\gamma_{2}=0.84,\gamma_{3}=1.25,\gamma_{4}=0.29,\gamma_{5}=5.49$

在这种情况下，在标准规定的范围内（89.1 至 11200 Hz），没有任何音调被标记为 "突出"，因此可以使用 PA 的等式（无音调）。

改善隔音效果

测量改进隔音后对测量声压级和感知噪声的影响

使用图形均衡器滤波器组进行模拟

设计一个 graphicEQ 对象来模拟拟议隔音设备的衰减。低频较难衰减，因此我们创建的模型最好在 200 赫兹以上。

geq = graphicEQ(Bandwidth="1 octave",SampleRate=FS,Gains=[-0.5 -1.25 -3.4 -7 -8.25 -8.4 -8 -7 -6.4 -5.6]);
cf = getCenterFrequencies(splMeter(Bandwidth="1 octave"));

显示 graphicEQ 对象的频率响应。

[B,A] = coeffs(geq);
sos = [B;A].';
[H,w] = freqz(sos,2^16,FS);
semilogx(w,db(abs(H)))
title("Frequency Response of Soundproofing Simulation Filter")
ylabel("Relative SPL (dB)")
xlabel("Frequency (Hz)")
xlim(cf([1,end]))
grid on

使用图形均衡器对发动机录音进行滤波，以模拟隔音效果。

x2 = geq(x);

比较使用和不使用隔音材料时的声压级。重复使用相同的声压级计设置，但使用经过过滤的录音。

reset(spl)
[LCFnew,~,LCpeaknew] = spl(x2);
plot(t,LCpeak,t,LCF,t,LCpeaknew,t,LCFnew)
legend("LCpeak (original)", ..."LCF (original)", ..."LCpeak (with soundproofing)", ..."LCF (with soundproofing)", ...Location="southeast")
title("SPL Measurement of Engine Noise")
xlabel("Time (seconds)")
ylabel("SPL (dB)")
ylim([70 95])
grid on

比较隔音前后的感知响度测量结果。