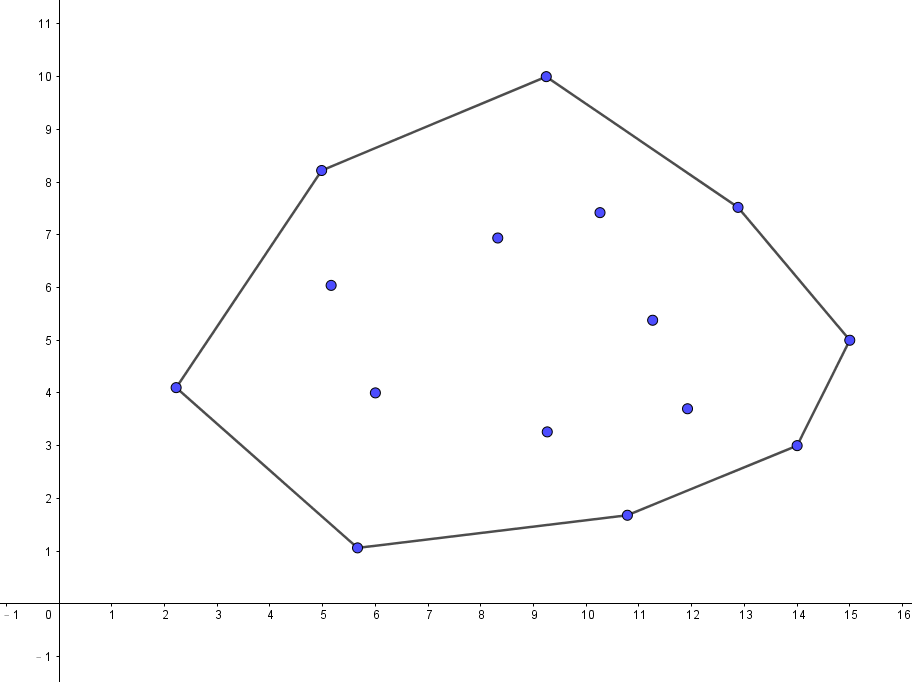
现在有一大堆点，然后你要找出一个可以围住这些点且面积最小的凸多边形，这个凸多边形称为凸包。

显而易见，如果要面积最小，那凸包的顶点势必得是这一大堆点的几个点，你也可以想成是用一条橡皮筋把这些点圈起来。

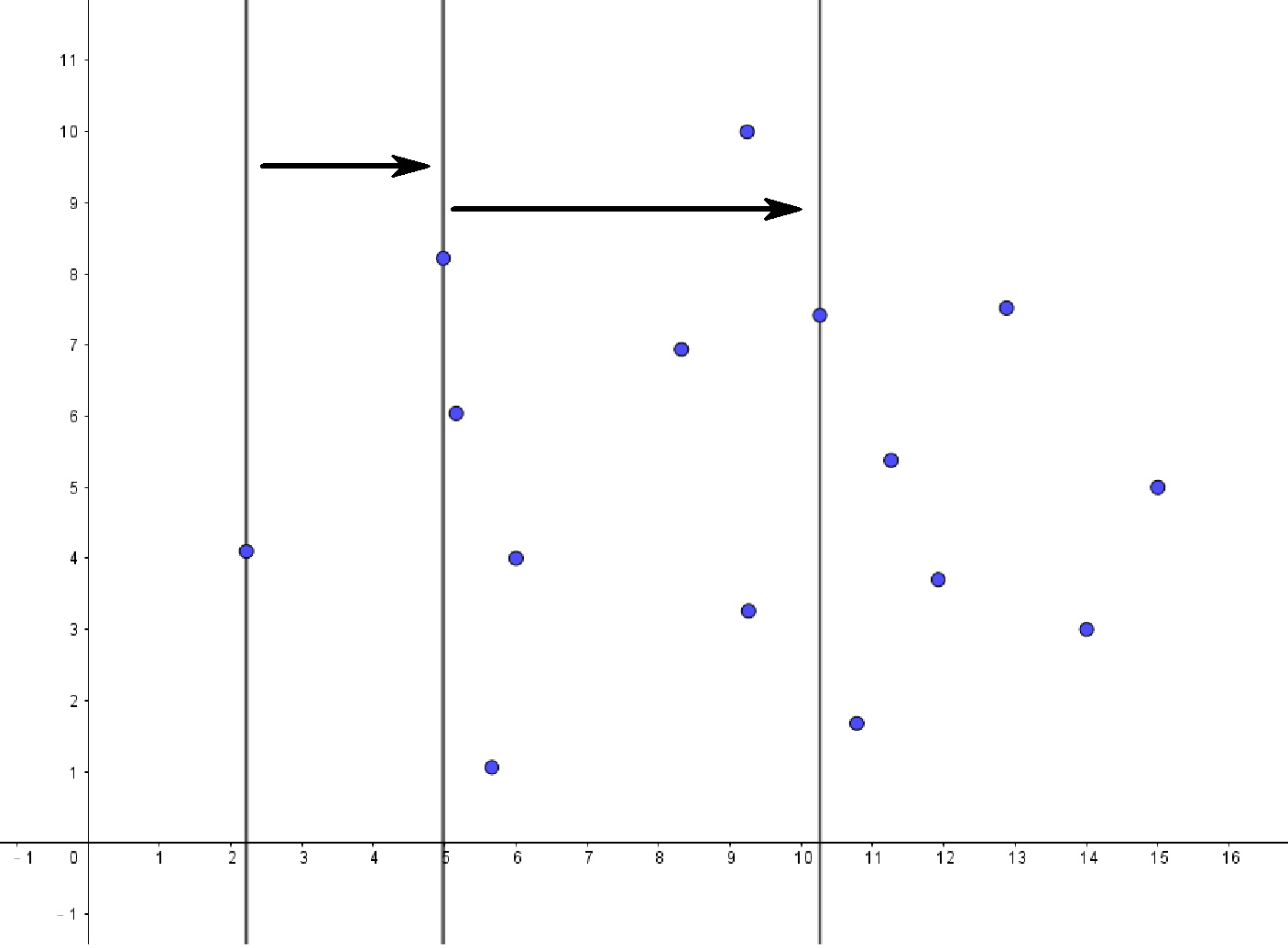
先把各个点按坐标从小到大排序，坐标相同则再按坐标从小到大排序，排序之后的点顺序会是由左至右、由下至上，这样一来我们就可以按这个顺序遍历这些点，这种往固定方向扫描的方式，称为扫描线。

先讨论一件事情：有一个凸多边形，它的顶点已经按逆时针顺序排好了，依次是 $p_1,p_2,...,p_n$ ，那么 $p_i$ 和 $p_j$ 与 $p_k$ 的关系会是什么（令 $i<j<k$既然是凸多边形，那么它的边应该是要一直往同个方向转弯的，而如果将边逆时针排序，这个边的斜率也应该是一直往逆时针方向转弯，显然点也会是这样，因此：

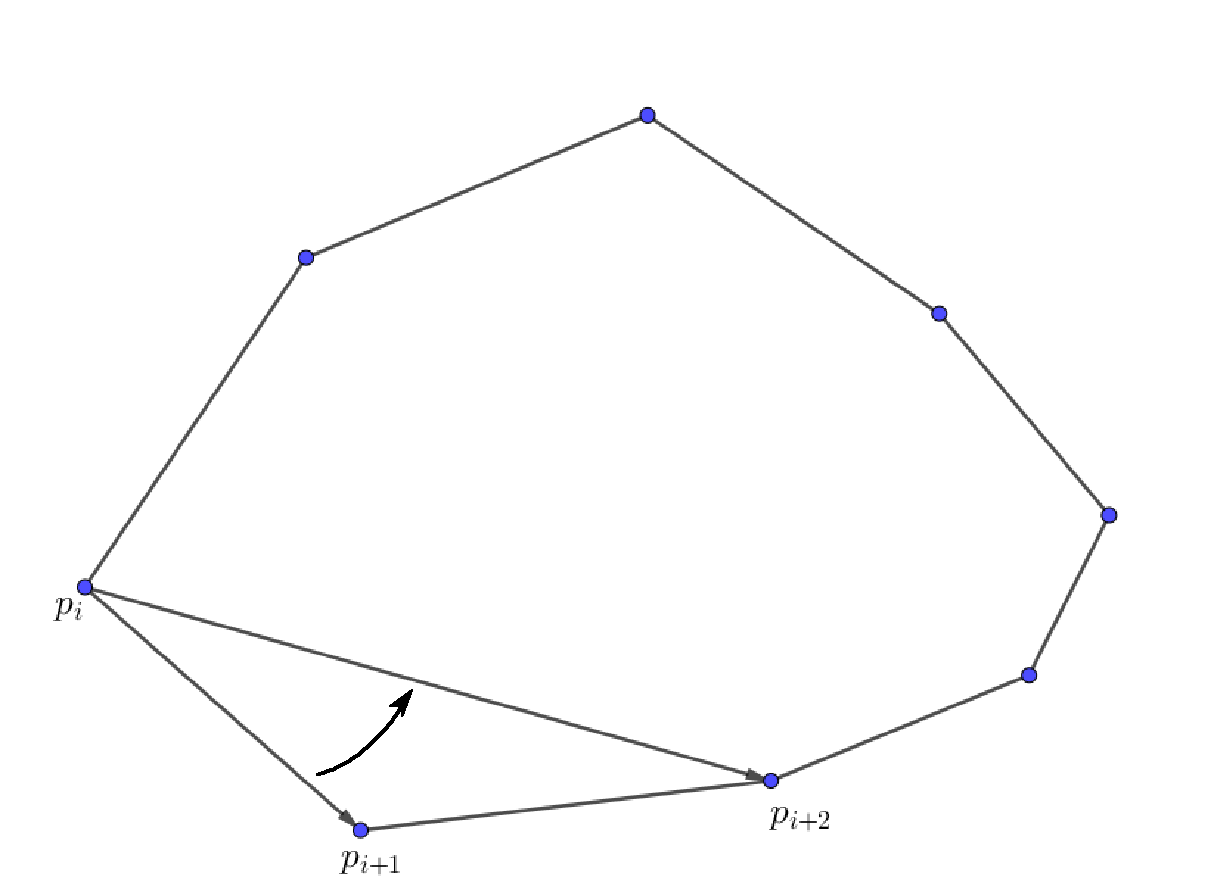
再来，我们把凸包分成上下两部分：上凸包和下凸包，以极左和极右点分割，如果极左点或极右点有两个（最多只会有两个），上面那个属于上凸包，下面那个属于下凸包，否则极左点必属于下凸包，极右点必属于上凸包。

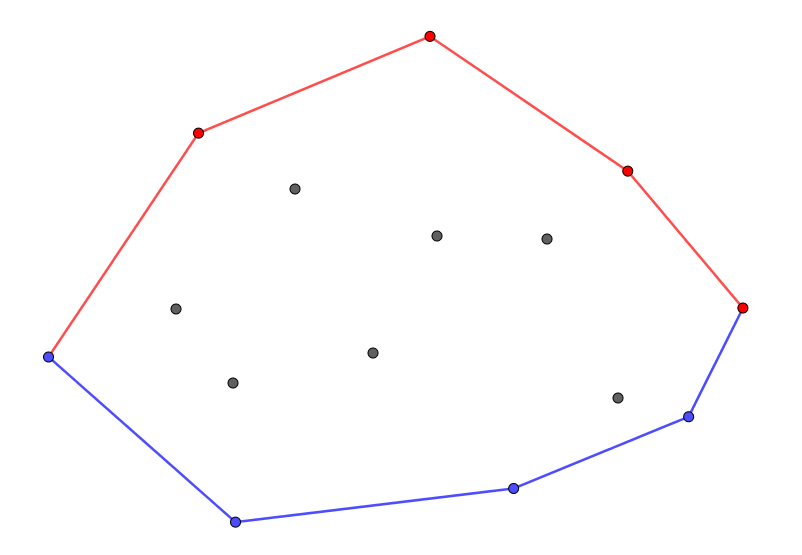
显然，上或下凸包中不会有 x 坐标相同的顶点，因此在上或下凸包中，每个顶点都能分别出左右的关系的，并且你会发现，如果把点按逆时针排序，在下凸包中的点也是由左而右排序的、在上凸包的点也是由右而左排序的。

这样一来左右关系就有用了，先用由左而右的扫描线把下凸包做出来，再用由右而左的扫描线把上凸包做出来，就可以得到整个凸包。

整个流程可以用一个栈来实现，在处理一个点的时候，我们尝试把它加进凸包里，此时这个点是 ( p ) ，栈顶的点是 ( top ) ，栈顶再往下一个点是 ( second ) ，把这些点代入刚刚的式子，符合条件或者栈大小小于 2 时就停止，否则就把栈顶 pop，然后继续重复，结束后就把目前处理中的点放入栈顶。

在做下凸包的时候，先从最左边且最下面的点开始做上述动作，做到最后，栈顶的点应该是最右边且最上面的点，把它 pop 掉，因为它应该属于上凸包；做上凸包的时候，从最右边且最上面的点开始做，最后栈顶会是最左且最下的点，把它 pop 掉后，这两个接起来就是完整的凸包。

因为要用到栈顶往下一个点，所以栈用 vector 来实现。

#include <bits/stdc++.h>#define mp(a, b) make_pair(a, b)
#define pb(a) push_back(a)
#define F first
#define S secondusing namespace std;template<typename T>
pair<T, T> operator-(pair<T, T> a, pair<T, T> b){return mp(a.F - b.F, a.S - b.S);
}template<typename T>
T cross(pair<T, T> a, pair<T, T> b){return a.F * b.S - a.S * b.F;
}template<typename T>
vector<pair<T, T>> getConvexHull(vector<pair<T, T>>& pnts){int n = pnts.size();sort(pnts.begin(), pnts.end());vector<pair<T, T>> hull;for(int i = 0; i < 2; i++){int t = hull.size();for(auto& pnt : pnts){while(hull.size() - t >= 2 && cross(hull.back() - hull[hull.size() - 2], pnt - hull[hull.size() - 2]) <= 0)hull.pop_back();hull.pb(pnt);}hull.pop_back();reverse(pnts.begin(), pnts.end());}return hull;
}

旋转卡尺

用旋转两条平行线、夹住一堆点，看在线上的点是哪些，就叫旋转卡尺。

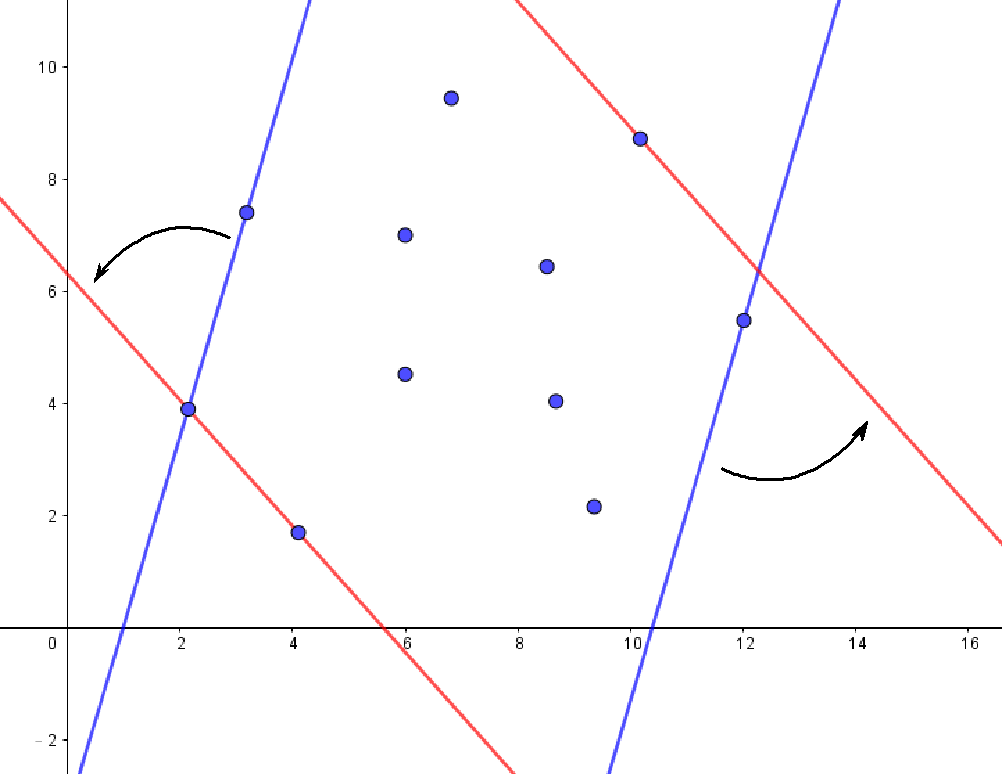
旋转线、夹点感觉很麻烦，是不是要用什么角度的东西啊？其实不用，先来分析一下问题，用两条平行线夹一堆点，那么平行线只会碰到凸包上的点而已，所以不在凸包上的点都可以先忽略：

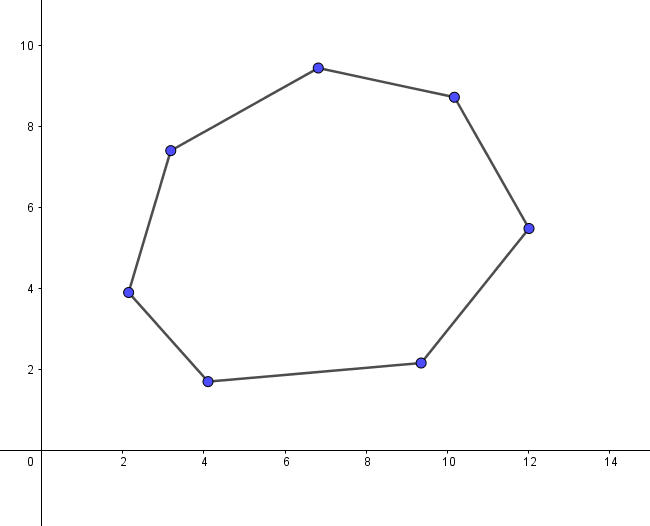
过一个点的直线有很多条，但是过一个线段的直线只有一条，所以先枚举线段，再去找和它平行的直线应该会夹到哪个点，这样问题就简单多了。要找平行线会碰到哪个点，显然离线段最远的点就是了。

不过算距离是另一个问题，听起来也很麻烦，但其实很简单。一个点距离一条直线的距离，等同于过该点在直线上作垂线段的长，而一开始选定的线段作为底、垂线段长作为高，那么就可以得一个平行四边形面积了，且底的长是固定的，只要枚举最远点，就等同于枚举高，而得出面积最大的，就是我们要求的最远点。

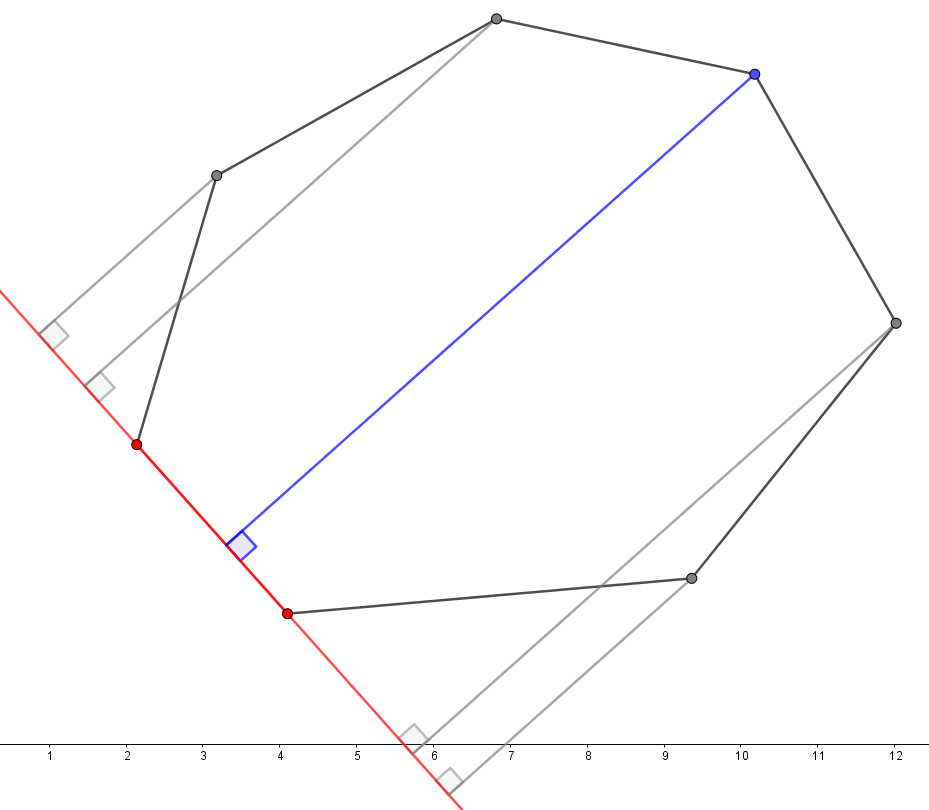
上图中，选定两个红色点所连成的线段为底，然后枚举各个顶点取高，得出蓝色垂线是最长的，因此蓝色点就是距离红色线段最远的点。

这就是旋转卡尺的基础应用——最远点对，找到距离每一线段最远的点，再取该点与线段两端点的距离取最大值，这样就可以得出所有点中最远的点对为何。

硬要这么做的方式，时间复杂度是 $O(n^3)$， $n$ 是凸包上点的数量（不计盖凸包的复杂度），枚举线段是 $O(n^2)$ ，再枚举一个点要再乘上 $n$ 。

这不够快，我们需要更有效率的方式。

仔细观察一下，点和线段的距离有一个规律——先渐大，到一个最大值，再渐小：

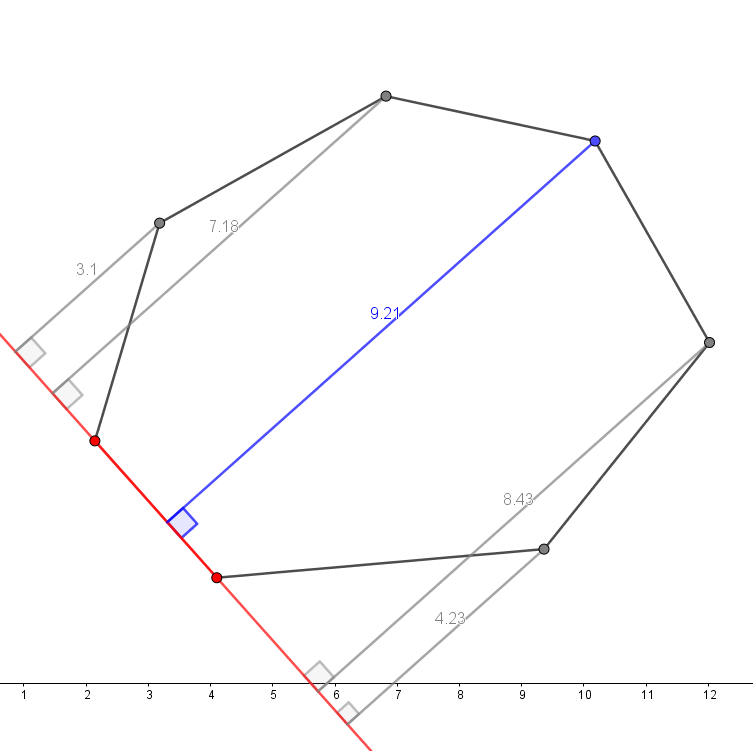
会发现它会呈现一个单峰函数，也就是一个先递增、再递减的函数，这样我们就可以三分搜找到最高点了，这样三分搜一次的复杂度是 $O(n)$，再乘上点的数量，就是 $O(n^2)$。

这样子还是不够快，前面提到旋转卡尺是「旋转两条平行线」，刚才的动作都是旋转其中一条，再去搜寻另一条，那我们可不可以在旋转其中一条的同时，把另一条一起旋转？答案是：可以。

（以下的转都是指往同一个方向转）
先找到距离第一条边最远的点，过前者的线称为第一条平行线，过后者的称为第二条平行线，接下来我们转动第一条平行线，也就是把它转到第二条线段上，而第二条平行线不要动，会发现，第一条平行线离第二条平行线那个点近了一些，接着再转第二条平行线，也就是把它转到下一个点上，那么距离会变远。

也就是，可以在不重新来过的情況下，找到单峰函数的最高点，会发现这样就是把两条平行线绕一圈，因此这样的复杂度是 $O(n)$ 。

原文地址：https://cp.wiwiho.me/convex-hull/