目录
1.红黑树
1.1红黑树的概念
1.2红黑树的性质
1.3红黑树节点的定义
1.4红黑树的插入操作
1.5红黑树的验证
1.6红黑树的删除
1.7红黑树与AVL树的比较
1.8红黑树的应用
1.红黑树
1.1红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
1.2红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
1.3红黑树节点的定义
我们将红色与黑色设置成枚举类型,使代码看起来更加规范,我们定义节点采用类模板的方式,内部成员分别是左节点指针,右节点指针,父亲节点指针,pair结构体类型的变量,然后就是代表我们颜色的变量。我们再对它们进行初始化列表就可以了,我们的每个节点初始颜色都得设置成红色,不然就无法满足我们上面给的5条红黑树的性质。
1.4红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
2. 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何 性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连 在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
情况一: cur为红,p为红,g为黑,u存在且为红
cur和p均为红,违反了性质三,此处能否将p直接改为黑?——不能
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
在我们搞清楚了插入的操做的原理之后,我们再来看它的代码就很容易明白了。
//插入bool Insert(const pair<K, value>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//调整红黑树//parent是黑的也直接结束while (parent && parent->_col == RED){//关键看叔叔Node* grandf = parent->_parent;if (parent == grandf->_left){Node* uncle = grandf->_right;//叔叔存在且为红,变色即可if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;grandf->_col = RED;//继续往上处理cur = grandf;parent = cur->_parent;}else//叔叔不存在,或则存在且为黑{// g// p u//cif (cur == parent->_left){parent->_col = BLACK;grandf->_col = RED;RotateR(grandf);}// g// p u// celse{RotateL(parent);grandf->_col = RED;cur->_col = BLACK;RotateR(grandf);}break;}}else{Node* uncle = grandf->_left;//叔叔存在且为红,变色即可if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;grandf->_col = RED;//继续往上处理cur = grandf;parent = cur->_parent;}else//叔叔不存在,或则存在且为黑{// g// u p// cif (cur == parent->_right){parent->_col = BLACK;grandf->_col = RED;RotateL(grandf);}// g// u p// celse{RotateR(parent);grandf->_col = RED;cur->_col = BLACK;RotateL(grandf);}break;}}}_root->_col = BLACK;return true;}看过我AVL树或则二叉搜索树文章的同学肯定对前半部分代码非常熟悉了,就是二叉搜索树的方式进行插入,接下来我们直接分析红黑树的调整部分的代码。
我们可以看到我们循环的条件是父亲节点不为空且是红的就要一直进行调整,根据我们所画的图,我们需要一个祖父节点,我们发现接下来是有一套if...else,这是判断父亲节点是祖父的左孩子还是右孩子,方便我们确定叔叔节点的位置,我们所画的图只是if的情况,else的情况我没有画的原因是只要你把if的逻辑弄懂了,那么else就是反一下,没有什么新的东西,我等会稍微讲一讲就清楚了,我们重新回到if里,这种情况,叔叔节点就是祖父的右孩子,按照情况一,叔叔存在且为红,那么我们只需要进行变色操作就可以了,如果叔叔不存在,或则存在且为黑,那么我们就需要进行旋转操作,按照情况二的图里,如果cur是在父亲的左子树,那么直接右旋就可以了,不要忘了父亲节点和祖父节点要变色,如果cur是在父亲的右子树方向,那么我们就要进行左旋,变色,再右旋就可以了,跟我们画的图的思路是一模一样的。有了这个思路再看我们else的代码就会发现除了把旋转方向对换一下,指针方向稍微改改,其他可以说是一模一样。
旋转代码:
//右旋void RotateR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR){SubLR->_parent = parent;}SubL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = SubL;if (parent == _root){_root = SubL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = SubL;}else if (ppnode->_right == parent){ppnode->_right = SubL;}SubL->_parent = ppnode;}}//左旋void RotateL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL){SubRL->_parent = parent;}SubR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = SubR;if (parent == _root){_root = SubR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = SubR;}else if (ppnode->_right == parent){ppnode->_right = SubR;}SubR->_parent = ppnode;}}右旋和左旋的代码讲解大家可以去看我的C++实现——AVL树那篇文章,这里的左旋右旋代码跟那里的是一模一样的,只不过少了行平衡因子的更新而已,因为红黑树不用平衡因子。
1.5红黑树的验证
红黑树的检测分为两步:
1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质
中序遍历代码:
//中序遍历void InOrder(){_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first<< ": " << root->_kv.second << endl;_InOrder(root->_right);}中序遍历就不用我多说什么了吧,就是按照左根右的方式进行递归就可以了。
判断是否是红黑树:
//判断是否平衡bool IsBalance(){if (_root->_col == RED){return false;}int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){refNum++;}cur = cur->_left;}return Check(_root, 0, refNum);}bool Check(Node* root, int blacknum,const int refnum){if (root == nullptr){if (refnum != blacknum){cout << "存在黑色节点不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << ": " << "存在红色连续" << endl;return false;}if (root->_col == BLACK){blacknum++;}return Check(root->_left, blacknum, refnum)&& Check(root->_right, blacknum, refnum);}判断是否是红黑树我们要按照它的5条性质去设计。
首先,判断根节点是不是黑的,不是直接返回false,接下来我们再来看其它性质是否满足,我们先计算出一条路径,然后交给check函数去做。
当一条路走完后,我们看一下黑色是不是一样多,一样多我们就返回true,否则返回false。我们还要看是否有连续的红色存在,有就返回false。
最后就是以递归的方式遍历每条路径,遇到黑色节点记录上就好了。
1.6红黑树的删除
红黑树的删除本节不做讲解,有兴趣的同学可参考:《算法导论》或者《STL源码剖析》
推荐博客:http://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html
1.7红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log_2 N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数, 所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
1.8红黑树的应用
1. C++ STL库 -- map/set、mutil_map/mutil_set
2. Java 库
3. linux内核
4. 其他一些库
C++实现——红黑树
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/404764.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Chat App 项目之解析(二)
Chat App 项目介绍与解析(一)-CSDN博客文章浏览阅读76次。Chat App 是一个实时聊天应用程序,旨在为用户提供一个简单、直观的聊天平台。该应用程序不仅支持普通用户的注册和登录,还提供了管理员登录功能,以便管理员可以…
初识指针4の学习笔记
目录 1>>前言
2>>字符指针变量
3>>数组指针变量
4>>函数指针变量
5>>函数指针数组
6>>回调函数是什么?
7>>结语 1>>前言 今天我会继续分享一些我做的笔记,以及我对指针的理解, 后续会…
Vue状态管理工具:vuex
目录 基本概念
使用步骤
核心概念
1.State
2.Getters
3.Mutations
4.Actions
5.Modules
辅助函数
基本概念
基础用法 基本概念
官方:Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式 库。它采用集中式存储管理应用的所有组件的状态,并以…
Android全面解析之context机制(三): 从源码角度分析context创建流程(下)
前言
前面已经讲了什么是context以及从源码角度分析context创建流程(上)。限于篇幅把四大组件中的广播和内容提供器的context获取流程放在了这篇文章。广播和内容提供器并不是context家族里的一员,所以他们本身并不是context,因而…
查找物理学领域文献的常用数据库
当我们查找文献时如果盲目去各个文献数据库查找不仅浪费时间和精力还不一定能找到自己需要的文献。我们需要对数据库有个简单的了解有方向的去寻找我们研究领域的文献资料,本文就向大家介绍一下查找物理学领域文献的数据库有哪些。
一、物理专业数据库(…
Android平台无纸化同屏如何实现实时录像功能
技术背景
我们在做无纸化同屏的时候,好多开发者采集到屏幕、麦克风|扬声器数据,除了需要推RTMP出去,或者启动个轻量级RTSP服务,对外提供个拉流的RTSP URL,别的终端过来拉流(小并发场景)&#x…
vue3基础ref,reactive,toRef ,toRefs 使用和理解
文章目录 一. ref基本用法在模板中使用ref 与 reactive 的区别使用场景 二. reactive基本用法在模板中使用reactive 与 ref 的区别使用场景性能优化 三. toRef基本用法示例在组件中的应用主要用途对比 ref 和 toRef 四. toRefs基本用法示例在组件中的应用主要用途对比 ref 和 t…
基于Arch的轻量级发行版Archcraft结合内网穿透实现远程SSH连接
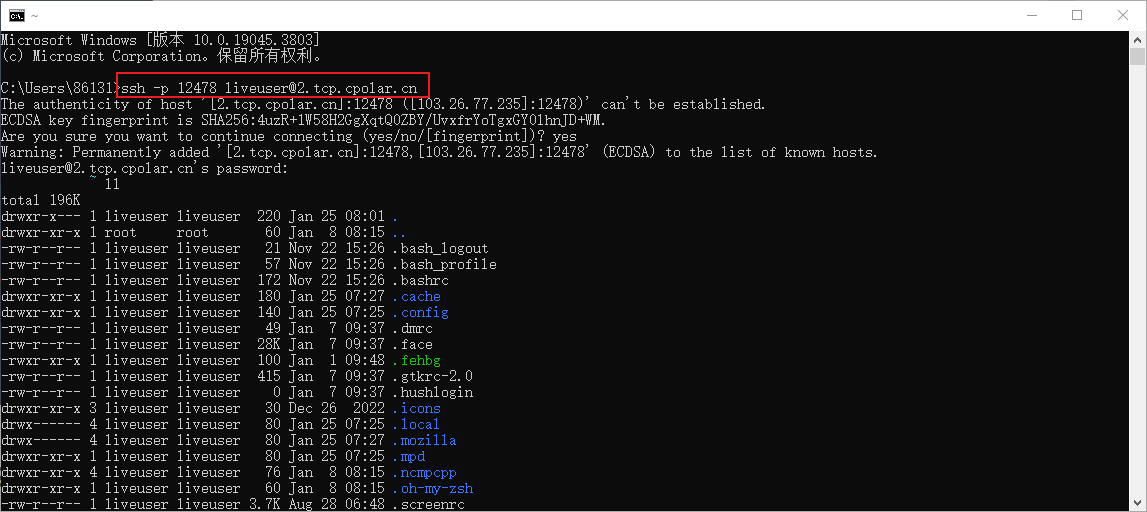
文章目录 前言1. 本地SSH连接测试2. Archcraft安装Cpolar3. 配置 SSH公网地址4. 公网远程SSH连接5. 固定SSH公网地址6. SSH固定地址连接 前言
本文主要介绍如何在Archcraft系统中安装Cpolar内网穿透工具,并以实现Windows环境ssh远程连接本地局域网Archcraft系统来说明使用内网…
高性能web服务器详解
一、Web服务的基础介绍
正常情况下单次web服务访问的流程简图: 1.1 Web服务介绍
这里介绍的是 Apache 和 NGINX
1.1.1 Apache 经典的Web服务端 Apache 起初由美国的伊利诺伊大学香槟分校的国家超级计算机应用中心开发 目前经历了两大版本分别是 1.X 和 2.X…
Mysql原理与调优-Mysql的内存结构
1.绪论
前面说过InnoDB每次查询数据或者更新数据,都是先以16kb的大小将数据读取到内存中,然后对内存中的数据页进行操作。为了减少磁盘IO,Innodb的会先单独的申请一块连续的空间,将从磁盘中的数据页缓存到这片内存中。这片内存就…
2D Inpainting 与NeRF 3D重建的多视角一致性问题
一 问题: NeRF依赖于输入图像的一致性。NeRF(Neural Radiance Fields)在生成三维场景时,依赖于从多个视角拍摄的输入图像之间的一致性来准确地推断场景的三维结构和颜色信息。 具体来说: 多视角一致性: Ne…
Hive3:三种常用的复杂数据类型
一、Array类型
1、数据示例 2、实操
元数据
zhangsan beijing,shanghai,tianjin,hangzhou
wangwu changchun,chengdu,wuhan,beijin创建表
CREATE TABLE myhive.test_array(name string, work_locations array<string>)
ROW FORMAT DELIMITED FIELDS TERMINATED BY \t…
LVM 使用以及配置
逻辑卷管理 (LVM) 是一种用于 Linux 系统的存储管理工具,比传统的磁盘分区方法更灵活。LVM 通过将物理存储设备组合成逻辑卷,使得磁盘空间的管理更加动态和便捷。它提供了物理层的抽象,让用户可以创建跨越多个物理磁盘或分区的逻辑卷。
LVM …
2024年软件测试经典面试题(全三篇)【包含答案】做完面试进入大厂不是梦
前言
迎来的便是金九银十,一直想着说分享一些软件测试的面试题,这段时间做了一些收集和整理,下面共有三篇经典面试题,大家可以试着做一下,答案附在后面,希望能帮助到大家。
软件测试经典面试题࿰…
【vue讲解:es6导入导出语法、 vue-router简单使用、登录跳转案例、scoped的使用、elementui使用】
1 es6导入导出语法
# 做项目:肯定要写模块--》导入使用# 默认导出和导入
在某个js中 # 命名导出和导入1.1 默认导出和导入
// #########导出语法###########
// export default name // 只导出变量
// export default add // 只导出函数// export default {nam…
android13顶部状态栏里面调节背光 背景闪烁问题
总纲
android13 rom 开发总纲说明
目录
1.前言
2.问题分析
3.代码分析
4.代码修改
5.彩蛋 1.前言 android13顶部状态栏里面调节背光, 背景闪烁问题,会出现画面不全问题,如下图 2.问题分析
这里看起来是由于隐藏的时候,界面显示是一个渐变的隐藏,但是后面的背景又是…
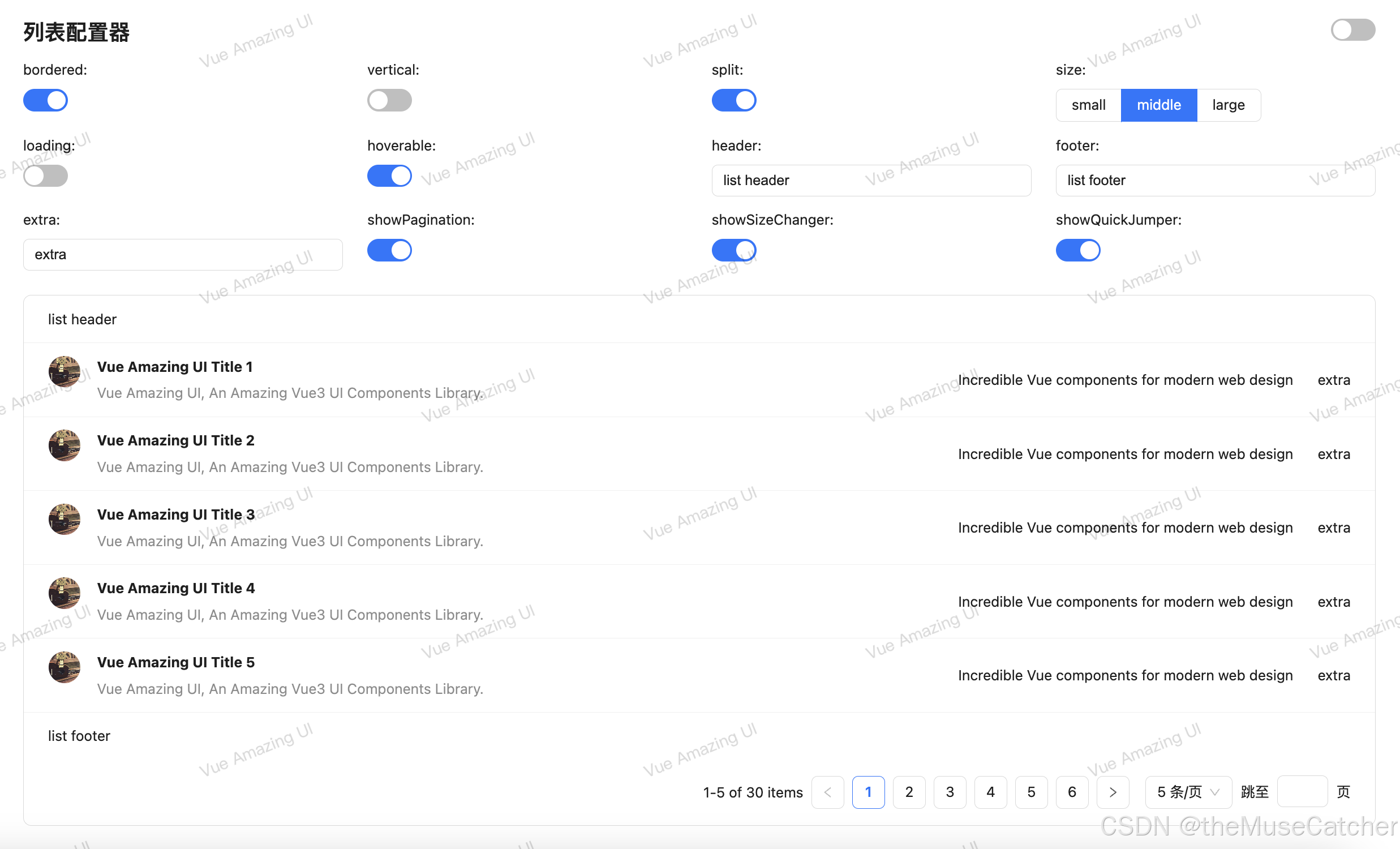
Vue3列表(List)
效果如下图:在线预览 APIs
List
参数说明类型默认值bordered是否展示边框booleanfalsevertical是否使用竖直样式booleanfalsesplit是否展示分割线booleantruesize列表尺寸‘small’ | ‘middle’ | ‘large’‘middle’loading是否加载中booleanfalsehoverable是否…
stripe Element 如何使用
这里要准备好几个东西:
一个支付成功过后的回调
还有一个下单的接口
一旦进入这个下单界面,就要去调下单的接口的,用 post,
这个 接口你自己写,可以写在后端中,也可以放到 nextjs 的 api 中。
首先说的是这个下单…
Linux ubuntu 24.04 运行《文明5》游戏,解决游戏中文设置的问题!
Linux ubuntu 24.04 运行《文明5》游戏,解决游戏中文设置的问题!
《文明5》是一款回合制经营策略游戏,拼的就是科技发展速度,点的是科技树,抢的就是科技制高点,但是真的是时间漫长,可能需要好几…
推荐文章
- NIFI汉化_替换logo_二次开发_Idea编译NIFI最新源码_详细过程记录_全解析_Maven编译NIFI避坑指南002
- python学习之变量类型
- # Go学习-Day10
- # 开发趋势 Java Lambda 表达式 第三篇
- #Day Day Plan# 《NCB_PCI_Express_Base 5.0.1.0》pdf 译文笔记 模版
- #基于一个小车项目的FREERTOS分析(一)系统时钟
- (13)配置飞行中的FFT(二)
- (Jmeter、Fiddler)脚本转换Loadrunner脚本
- (产品分析)KFC肯德基APP分析报告
- (超详细)字符函数和字符串函数【上】
- (单机版)神魔大陆|v0.51.0|冰火荣耀
- (二)Web服务器之Linux多进程