看到这句话的时候证明:此刻你我都在努力
加油陌生人

个人主页:Gu Gu Study
专栏:用Java学习数据结构系列
喜欢的一句话: 常常会回顾努力的自己,所以要为自己的努力留下足迹
喜欢的话可以点个赞谢谢了。
作者:小闭
前言
今天这篇文章是二叉树的第二篇文章,上一篇文章已经简单讲述了二叉树的各种遍历方法了,那么接下来就需要进阶一下,开始用二叉树的知识解决更多问题。如有哪里出现错误也欢迎指出唔。
那么我们先来开始我们今天的第一道小菜。
根据中序遍历和后序遍历写出前序遍历
设一课二叉树的 中序遍历序列:badce,后序遍历序列:bdeca
那么我们如何下手呢?首先我们先根据我们的知识来得出一些关键点。
- 后序遍历的最后一个节点就是根节点
- 那么我们就可以根据根节点在中序遍历中得出树的左右两边的节点
- 根据得出的信息开始逐渐还原树的样子,然后就可以根据树的样子得出前序遍历的顺序。
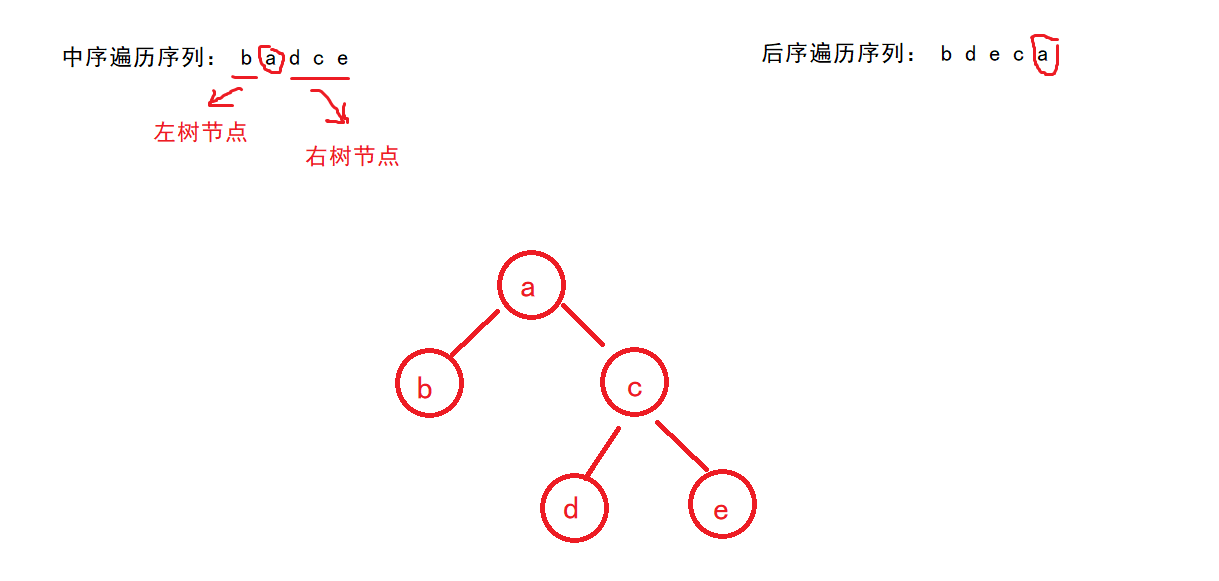
根据信息得出树,然后核对一下已知的连个遍历序列是否正确,如果正确那么我们就可以写出前序遍历的顺序了。
获取树的节点个数
我们既然要获取节点个数那么肯定需要我们取遍历这棵树了,除非你在这棵树创建加了个size变量来计数。
那么如果我们的树没有定义一个计数变量我们就必须得遍历这棵树了。
int size(BTNode root) {if (root == null) {return 0;}return size(root.left) + size(root.right) + 1;}我采用的是递归的方法,假设把每个节点都当作根节点(即假设该节点上方的节点是不存在的),那么他这棵树的节点树就等于左树的节点数加上右树的节点树加上1(这个1就是该节点本身)。代码的实现就如上面所示。
获取叶子节点的个数
获取节点数是比较简单的那么我们现在来进阶一下,我们来求一下一颗树的叶子节点个数,那么这样我们又该怎么操作呢?
首先我们需要先知道什么是叶子节点,叶子节点就是最后一层树的节点即:该节点既没有左孩子也没有右孩子。
那么根据这个关键点就可以写出代码了,当然我们还是需要遍历这棵树的。
int getLeafNodeCount(BTNode root) {if (root == null) {return 0;} else if (root.left == null && root.right == null) {return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}那么还是整棵树的叶子节点等于左树的叶子节点加上右树的叶子节点。
获取第K层节点的个数
那么我们要知道第k层的节点就需要想如何定位到第k层。
首先我们可以想着用一个整型变量来作为标记,当该变量为某个数时就表示该层就是第k层。既然要知道节点的个数那么遍历肯定是必不可少的。那么我们就用形参作为标记,当k==1时我们就返回1即可。
int getKLevelNodeCount(BTNode root, int k) {if (root == null||k<1) {return 0;}if (k == 1) {return 1;}return getKLevelNodeCount(root.left, k - 1)+getKLevelNodeCount(root.right, k - 1);}求二叉树的高度
求数的高度我们需要先 捋清思路:
首先我们要知道树的高度也可以说是树有几层,那么我们只需要挑出一条最高的一条路的高度即可
那么我们就一直遍历,每遍历多一层就+1,直到节点为null,然后我们就对比是左树的高还是右树的高度高,挑出最高的那个进行返回即可。
int getHeight(BTNode root) {if (root == null) {return 0;}int n1 = getHeight(root.left) + 1;int n2 = getHeight(root.right) + 1;return n1 > n2 ? n1 : n2;}二叉树层序遍历
那么首先我们要知道什么是层序遍历,层序遍历就比上一篇的三种遍历稍微简单,而且比较好理解
层序遍历就是将一颗树从上到下,从左到右开始遍历,一层一层遍历,每一层都是从左边遍历到右边
那么举一个例子吧:

想这么一颗二叉树它层序遍历的结果就是1 2 4 3 5 6,所以说是从上到下,从左到右开始遍历,一层一层遍历,每一层都是从左边遍历到右边。
那么代码如何实现呢?这里我们就需要到一个队列来实现了,我们在循环中将每个树的节点的左右孩子依次add到队列中,然后每次循环都出一个队列数据。那么根据思路就可以写出下面的代码了:
//层序遍历
void levelOrder(BTNode root) {if (root == null) {return;}Queue<BTNode> queue = new LinkedList();queue.add(root);while (!queue.isEmpty()) {BTNode node = queue.poll();System.out.print(node.value + " ");if (node.left != null) {queue.add(node.left);if (node.right != null) {queue.add(node.right);}}}}判断一棵树是否为完全二叉树
前面已经说过什么是完全二叉树了。现在温习一下吧。
完全二叉树:如果一个二叉树的所有层都被完全填满,除了最后一层,并且最后一层的节点尽可能地集中在左侧,这样的二叉树称为完全二叉树。
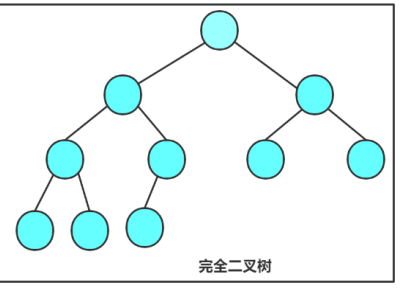
也就是说在如果最后一层在左边没有填满,右边就突然有一个节点,那么他就不是完全二叉树。如下就不是一棵完全二叉树:
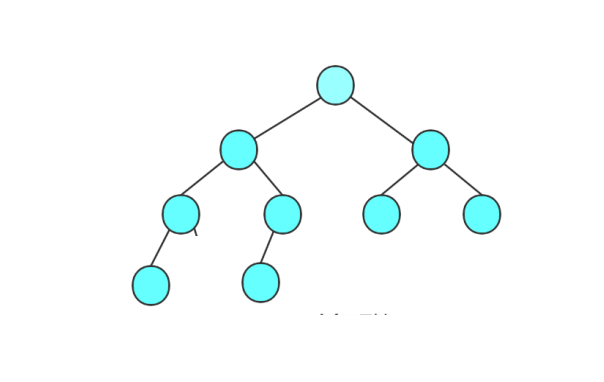
那么代码又要如实现判断一棵树是否是完全二叉树呢。
首先我们想到其实完全二叉树也需要从上到下,从左到右进行观察,看有没有同一层的节点是相隔一个节点或以上的。那么我们就可以从层序遍历的代码里进寻求灵感进行改动。
// 判断一棵树是不是完全二叉树
boolean isCompleteTree(BTNode root) {if (root == null) {return true;}Queue<BTNode> queue = new LinkedList();queue.add(root);while (!queue.isEmpty()) {BTNode node = queue.poll();if(node==null) {break;}queue.add(node.left);queue.add(node.right);}while (!queue.isEmpty()){BTNode node=queue.poll();if(node!=null){return false;}}return true;
}我们在循环体中不在判断node的左右孩子是否为空,而是无条件add到队列,然后在node为空的时候就break,如果这时这棵树是完全二叉树那么这时的队列里面的数据就会是n个null(注意null也是队列里的数据,也可以add进队列,这时队列不是空的),我们只需判断剩下的队列里面的成员是否全为null,如果是说明它是一颗完全二叉树否则就不是。
判断两颗二叉树是否相等
正如标题所写如何判断两棵二叉树是否相等,实现也是比较简单的,在判断节点是否为null的问题后,在判断值是否相等即可,然后进行递归
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p==null&&q!=null||q==null&&p!=null){return false;}if(p==null&&q==null){return true;}if(p.val!=q.val){return false;}return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}
}是不是一棵子树
给定你两条树的根节点,判断其中一颗是不是另一颗的子树,这个代码又该如何写呢?
写这道题的时候,看见了一位大佬的方法是比较厉害的,所以打算就用他的优质方法给你们进行讲解。
首先我们要判断是不是子树,那么按正常情况来说,在两棵树都不为null的情况下,他们如果存在子树关系,那么那颗比较大的树就会从某个节点开始和子树的节点完全相同,直到子树为null。
然后看到相同两个字我们是不是又可以用到上面的求两颗树是否相同的方法。如果不是从这个节点开始相同,那么就往左右两个孩子节点判断。
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}class Solution {public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(subRoot==null){return true;}if(root==null){return false;}return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot)||isSame(root,subRoot);}public boolean isSame(TreeNode root, TreeNode subRoot) {if(root==null&&subRoot==null){return true;}if(root==null||subRoot==null){return false;}if(root.val!=subRoot.val){return false;}return isSame(root.left,subRoot.left)&&isSame(root.right,subRoot.right);}}思路:先判断不正常情况下,即两棵树是否为null的情况。然后开始递归大的树的节点即可。
这段代码中其中最精妙的地方就是这个语句。
return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot)||isSame(root,subRoot);