续

5.4.4 LSTM 举例

网络里面只有一个 LSTM 的单元，输入都是三维的向量，输出都是一维的输出。这三维的向量跟输出还有记忆元的关系是这样的。假设 x2 的值是 1 时， x1 的值就会被写到记忆元里；假设 x2 的值是-1 时，就会重置这个记忆元；假设 x3 的值为 1 时，才会把输出打开，才能看到输出，看到记忆元的数字（记住！！！）
假设原来存到记忆元里面的值是 0，当第二个维度 x2 的值是 1 时， 3 会被存到记忆元里面去。第四个维度的 x2 等于，所以 4 会被存到记忆元里面去，所以会得到 7。第六个维度的x3 等于 1，这时候 7 会被输出。第七个维度的 x2 的值为-1，记忆元里面的值会被洗掉变为 0。第八个维度的 x2 的值为 1，所以把 6 存进去，因为 x3 的值为 1，所以把 6 输出。

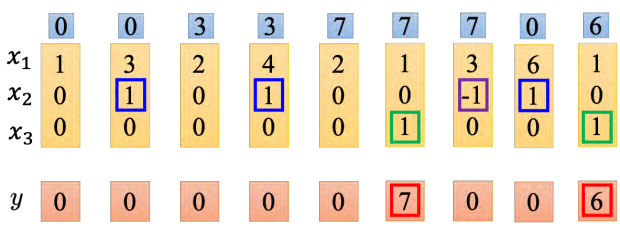
5.4.5 LSTM 运算示例

如果输入门被打开，则新的信息可以进入记忆元；如果遗忘门被打开，则旧的信息可以从记忆元中删除；如果输出门被打开，则记忆元中的信息可以被输出。
记忆元的四个输入标量是这样来的：输入的三维向量乘以线性变换（linear transform）后所得到的结果， x_1, x_2_, x_3 乘以权重再加上偏置。

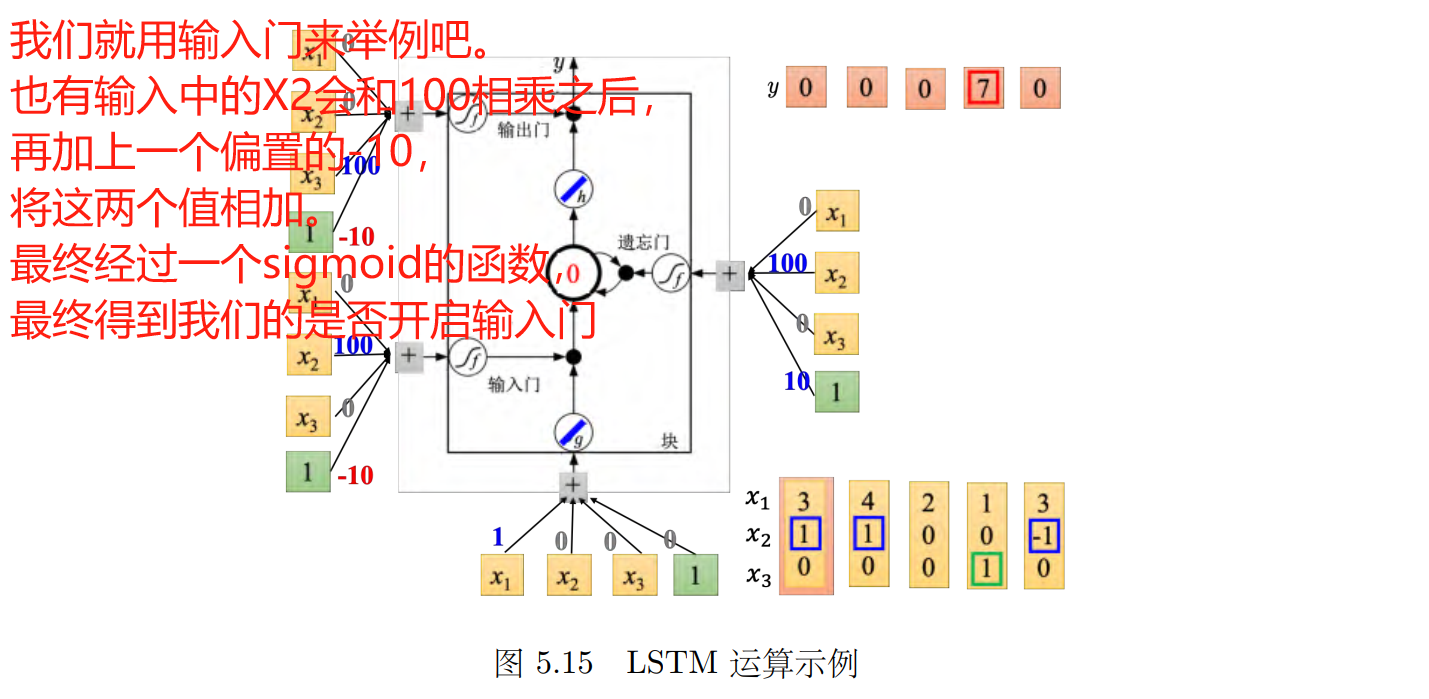
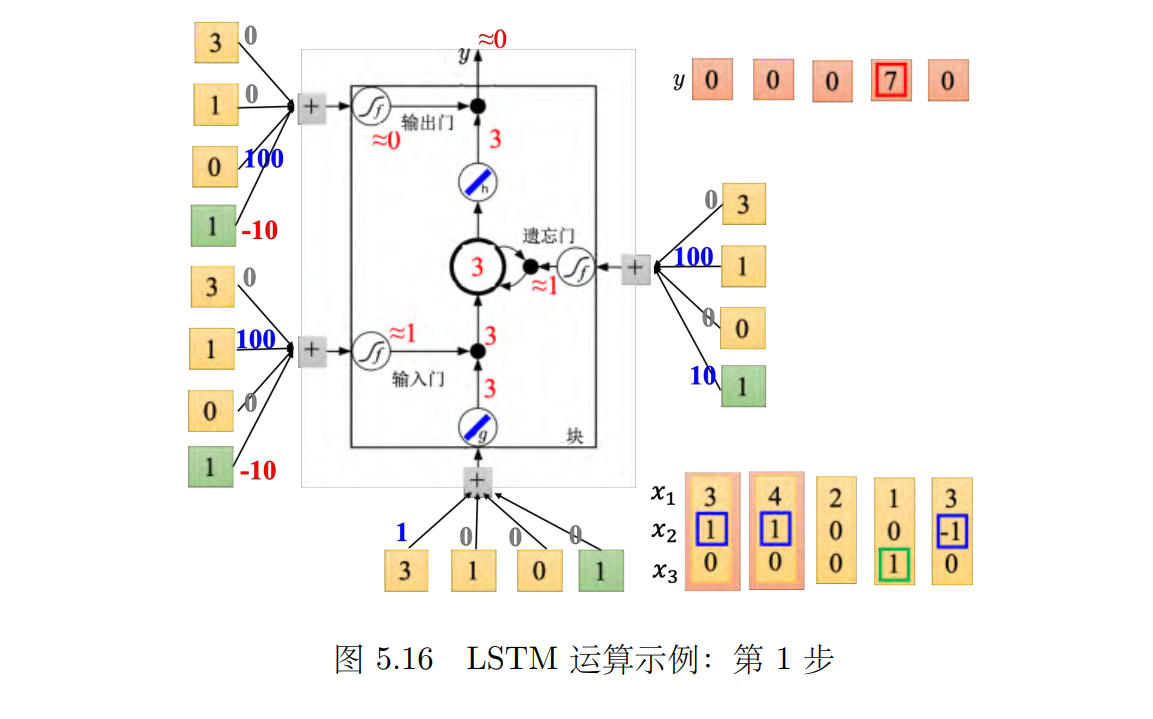
实际的输入一下看看。为了简化计算，假设 _g _和 _h 都是线性的。假设存到记忆元里面的初始值是 0，如图 5.17 所示，输入第一个向量 [3, 1, _0]T，输入这边 3*1=3，这边输入的是的值为 3。输入门这边 (1 _∗ _100 _- _10 _≈ _1) 是被打开 (输入门约等于 1)。 (g(z) ∗ f(zi) = 3)。遗忘门 (1 _∗ _100 + 10 _≈ _1) 是被打开的 (遗忘门约等于 1)。 0 *1+3=3(_c′ = g(z)f(zi) + cf(zf))，所以存到记忆元里面的为 3。输出门 (-10) 是被关起来的，所以 3 无关通过，所以输出值为 0。
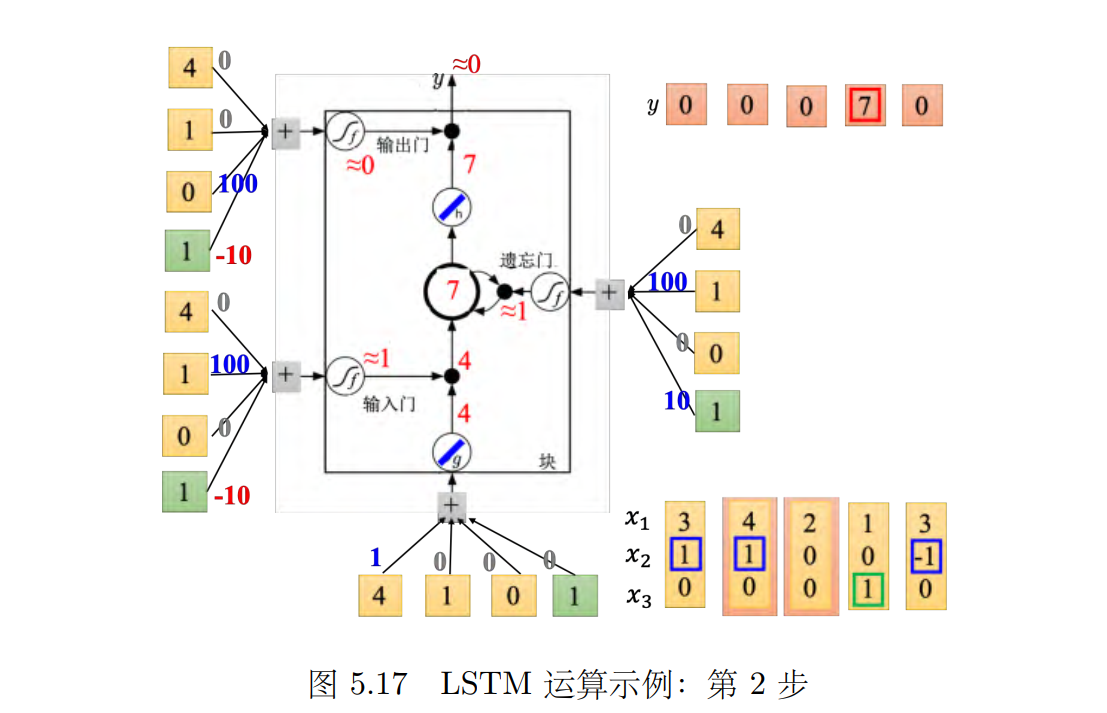
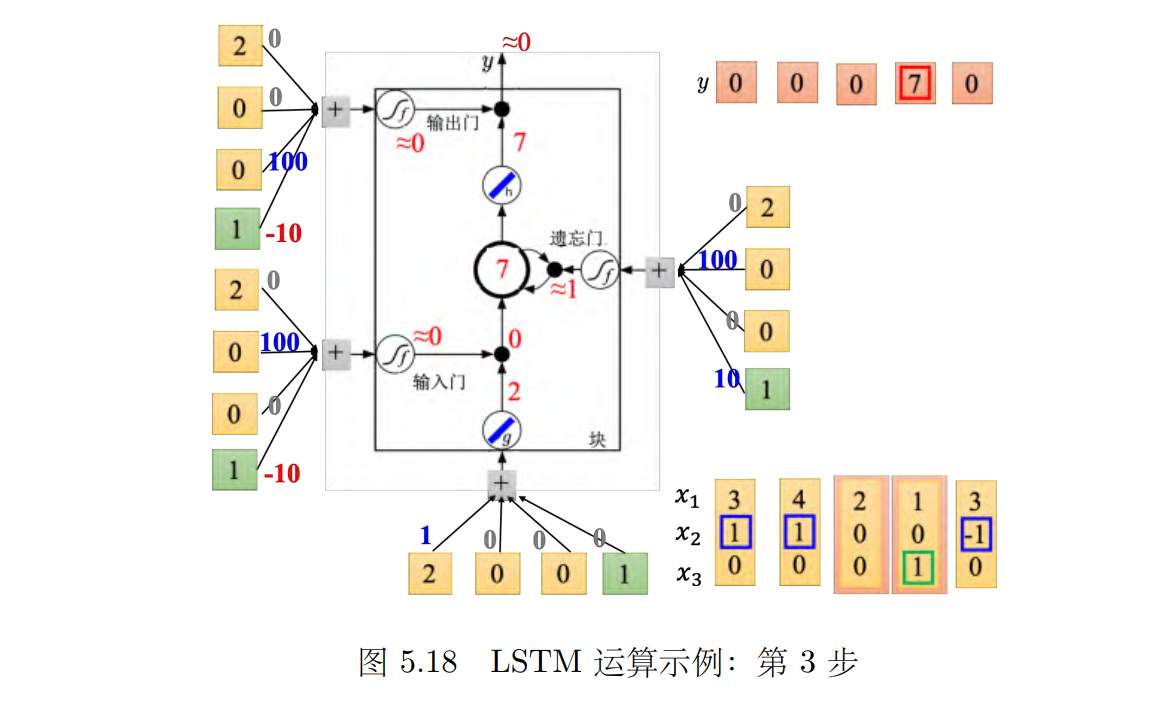
接下来输入 [4, 1, 0]T，如图 5.17 所示，传入输入的值为 4，输入门会被打开，遗忘门也会被打开，所以记忆元里面存的值等于 7（3 + 4 = 7），输出门仍然会被关闭的，所以 7 没有办法被输出，所以整个记忆元的输出为 0。接下来输入 [2, 0, _0]T，如图 5.18 所示，传入输入的值为 2，输入门关闭（_≈ _0），输入被输入门给挡住了（0 _× _2 = 0），遗忘门打开（10）。原来记忆元里面的值还是 7（1 _× 7 + 0 = 7）。输出门仍然为 0，所以没有办法输出，所以整个输出还是 0。
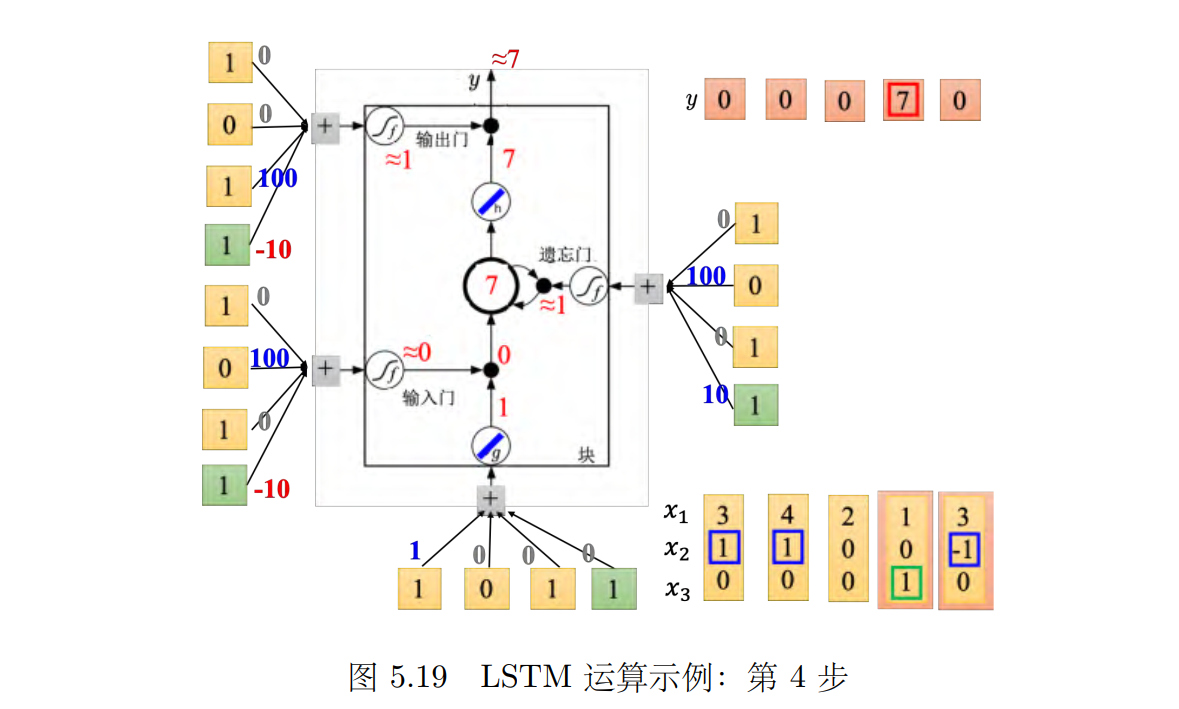
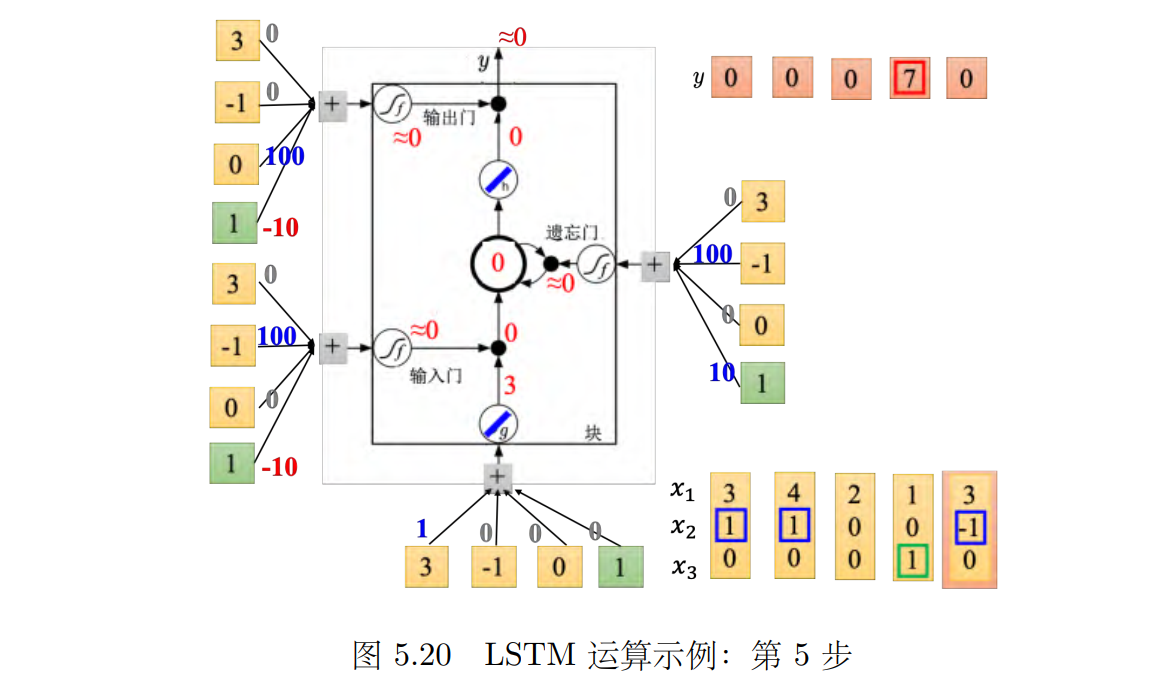
接下来输入 [1, 0, 1]T，如图 5.19 所示，传入输入的值为 1，输入门是关闭的，遗忘门是打开的，记忆元里面存的值不变，输出门被打开，整个输出为 7，记忆元里面存的 7 会被读取出来。最后输入 [3, -1, _0]T，如图 5.20 所示，传入输入的值为 3，输入门关闭，遗忘门关闭，记忆元里面的值会被洗掉变为 0，输出门关闭，所以整个输出为 0。
下面是详细步骤，包括每一步：

5.5 LSTM 原理

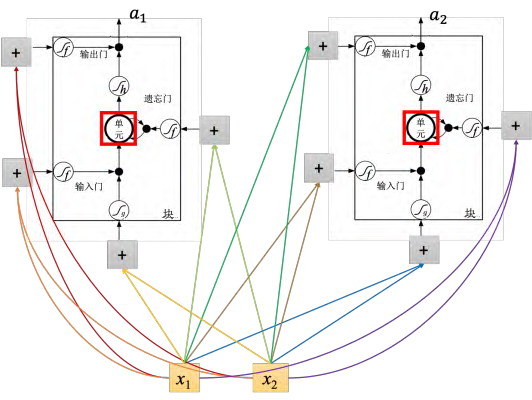
与传统的神经网络不同，LSTM需要四个输入来产生一个输出，并且需要四个不同的权重来操控每个记忆元的输入、输出、忘记和更新。此外，LSTM还需要四个不同的矩阵来进行线性变换，其中第一个矩阵将输入向量转换成控制每个记忆元输入的向量，而其他三个矩阵则用于控制每个记忆元的状态。由于LSTM需要四个输入和四个矩阵，因此它的参数量比一般的神经网络多出四倍。
为了简化，假设隐藏层只有两个神经元，输入 x_1, x_2 会乘以不同的权重当做 LSTM 不同的输入。输入 (x_1, x_2) 会乘以不同的权重会去操控输出门，乘以不同的权重操控输入门，乘以不同的权重当做底下的输入，乘以不同的权重当做遗忘门。第二个 LSTM也是一样的。

如图 5.23 所示，假设有一整排的 LSTM，这些 LSTM 里面的记忆元都存了一个值，把所有的值接起来就变成了向量，写为 _ct-_1（一个值就代表一个维度）。现在在时间点 t，输入向量 xt，这个向量首先会乘上一矩阵（线性变换）变成一个向量 z，向量 _**z **_的维度就代表了操控每一个 LSTM 的输入。 _**z **_这个维度正好就是 LSTM 记忆元的数量。 _**z **_的第一维就丢给第一个单元。这个 _xt _会乘上另外的一个变换得到 zi，然后这个 _zi _的维度也跟单元的数量一样， _zi _的每一个维度都会去操控输入门。遗忘门跟输出门也都是一样，不再赘述。所以我们把 _xt _乘以四个不同的变换得到四个不同的向量，四个向量的维度跟单元的数量一样，这四个向量合起来就会去操控这些记忆元运作。

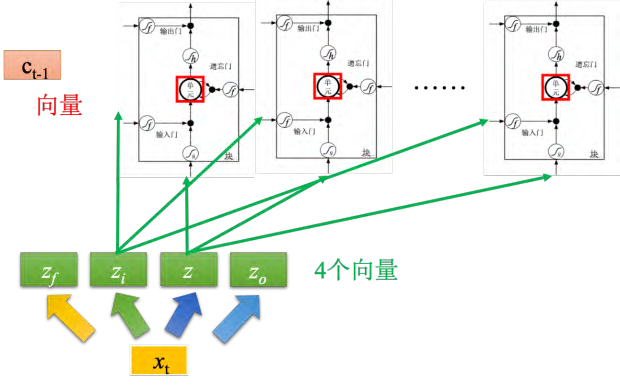
如图 5.24 所示，输入分别就是 z, zi, zo, zf(都是向量)，丢到单元里面的值其实是向量的一个维度，因为每一个单元输入的维度都是不一样的，所以每一个单元输入的值都会是不一样。所以单元是可以共同一起被运算的。 _zi _通过激活函数跟 _**z _相乘， _zf _通过激活函数跟之前存在单元里面的值相乘，然后将 _z _跟 _zi _相乘的值加上 _zf _跟 _ct-_1 相乘的值， _zo 通过激活函数的结果输出，跟之前相加的结果再相乘，最后就得到了输出 yt。

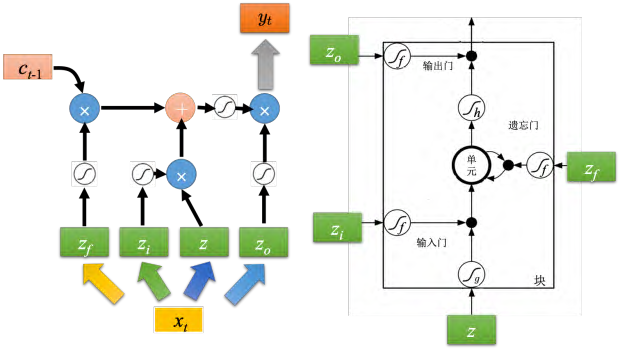
**之前那个相加以后的结果就是记忆元里面存放的值 ct，这个过程反复的进行，在下一个时间点输入xt+1，把 z 跟输入门相乘，把遗忘门跟存在记忆元里面的值相乘，将前面两个值再相加起来，在乘上输出门的值 ，得到下一个时间点的输出 yt+1 但这还不是 LSTM 的最终形态，真正的 LSTM 会把上一个时间的输出接进来，当做下一个时间的输入，即下一个时间点操控这些门的值不是只看那个时间点的输入 _xt _，还看前一个时间点的输出 _ht 。其实还不止这样，还会添加 peephole 连接，如图 5.25 所示。 peephole 就是把存在记忆元里面的值也拉过来。操控 LSTM 四个门的时候，同时考虑了 xt+1, ht, ct _，把这三个向量并在一起乘上不同的变换得到四个不同的向量再去操控 LSTM。

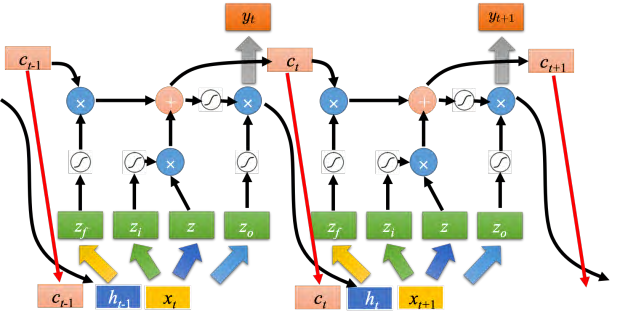
LSTM 通常不会只有一层，若有五六层的话，如图 5.26 所示。 一般做 RNN 的时候，其实指的就用 LSTM。

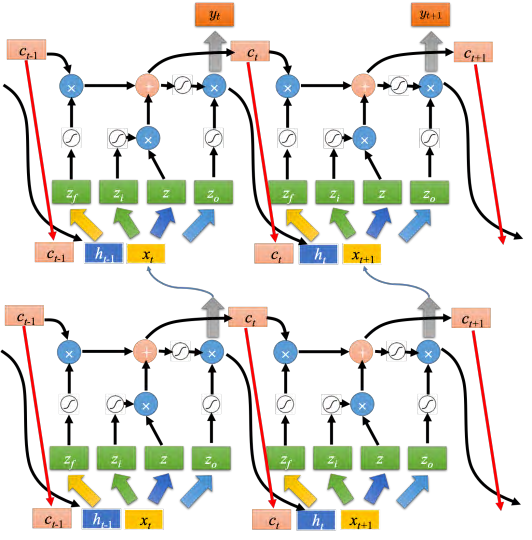
门控循环单元（Gated Recurrent Unit， GRU）是 LSTM 稍微简化的版本，它只有两个门。虽然少了一个门，但其性能跟 LSTM 差不多，少了 1/3 的参数，也是比较不容易过拟合

5.6 RNN 学习方式

以槽填充为例，首先需要给定一些句子并为其标注标签，告诉机器哪些单词属于哪个槽。接着，循环神经网络会根据输入的单词得到一个输出，再将其与参考向量计算交叉熵，期望输出与参考向量的距离越近越好。损失函数的输出和参考向量的交叉熵之和就是需要最小化的对象。

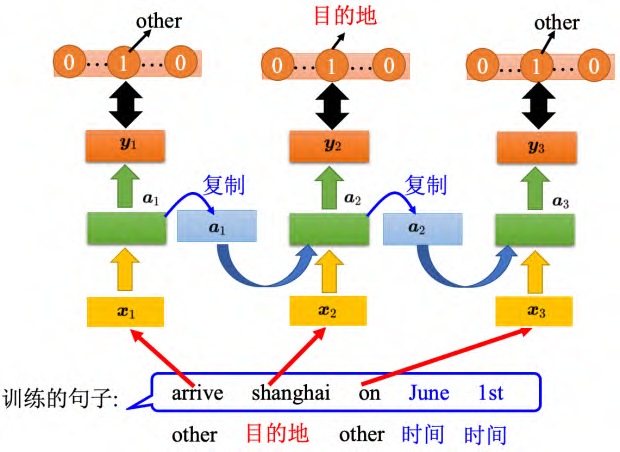
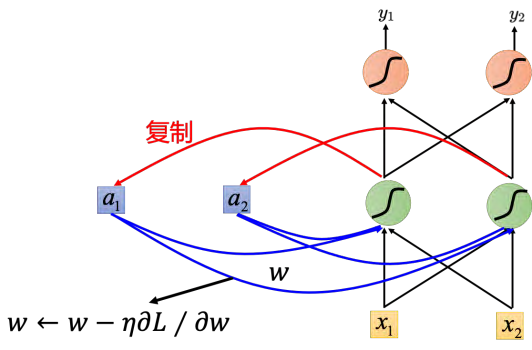
有了这个损失函数以后，对于训练也是用梯度下降来做。也就是现在定义出了损失函数_L_，要更新这个神经网络里面的某个参数 w，就是计算对 _w 的偏微分，偏微分计算出来以后，就用梯度下降的方法去更新里面的参数。梯度下降用在前馈神经网络里面我们要用一个有效率的算法称为反向传播。循环神经网络里面，为了要计算方便，提出了反向传播的进阶版，即随时间反向传播（BackPropagation Through Time， BPTT）。 BPTT 跟反向传播其实是很类似的，只是循环神经网络它是在时间序列上运作，所以 BPTT 它要考虑时间上的信息

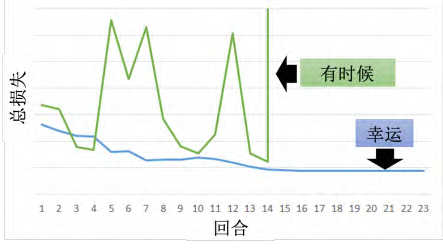
RNN 的训练是比较困难的，如图 5.29 所示。一般而言，在做训练的时候，期待学习曲线是像蓝色这条线，这边的纵轴是总损失（total loss），横轴是回合的数量，我们会希望随着回合的数量越来越多，随着参数不断的更新，损失会慢慢地下降，最后趋向收敛。但是不幸的是，在训练循环神经网络的时候，有时候会看到绿色这条线。如果第一次训练循环神经网络，绿色学习曲线非常剧烈的抖动，然后抖到某个地方，我们会觉得这程序有 bug。

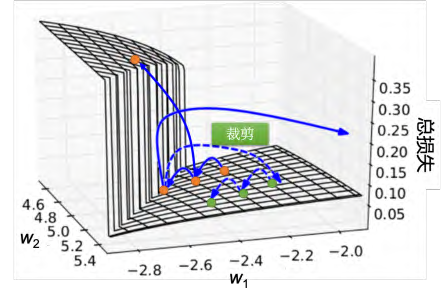
如图 5.30 所示， RNN 的误差表面是总损失的变化是非常陡峭的或崎岖的。误差表面有一些地方非常平坦，一些地方非常陡峭。纵轴是总损失， x 和 y 轴代表是两个参数。这样会造成什么样的问题呢？假设我们从橙色的点当做初始点，用梯度下降开始调整参数，更新参数，可能会跳过一个悬崖，这时候损失会突然爆长，损失会非常上下剧烈的震荡。有时候我们可能会遇到更惨的状况，就是以正好我们一脚踩到这个悬崖上，会发生这样的事情，因为在悬崖上的梯度很大，之前的梯度会很小，所以措手不及，因为之前梯度很小，所以可能把学习率调的比较大。很大的梯度乘上很大的学习率结果参数就更新很多，整个参数就飞出去了。裁剪（clipping）可以解决该问题，当梯度大于某一个阈值的时候，不要让它超过那个阈值

一个例子：之前讲过 ReLU 激活函数的时候， **梯度消失（vanishing gradient） **来源于 Sigmoid 函数。但 RNN 会有很平滑的误差表面不是来自于梯度消失。把 Sigmoid 函数换成 ReLU，其实在 RNN 性能通常是比较差的，所以激活函数并不是关键点。有更直观的方法来知道一个梯度的大小，可以把某一个参数做小小的变化，看它对网络输出的变化有多大，就可以测出这个参数的梯度大小，如图 5.31 所示。

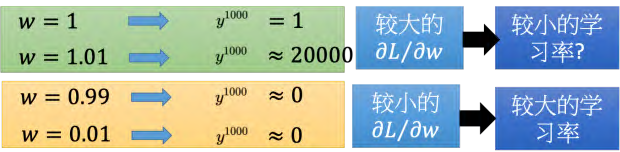
举一个很简单的例子，只有一个神经元，这个神经元是线性的。输入没有偏置，输入的权重是 1，输出的权重也是 1，转移的权重是 w。也就是说从记忆元接到神经元的输入的权重是 w。如图 5.32 所示，

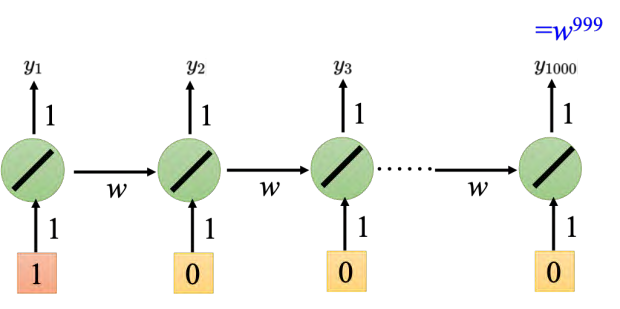
假设给神经网络的输入是 [1, 0, 0, _0]T，比如神经网络在最后一个时间点（1000 个输出值是 _w_999）。假设 _w _是要学习的参数，我们想要知道它的梯度，所以是改变 _w _的值时候，对神经元的输出有多大的影响。假设 _w _= 1， _y_1000 = 1，假设 _w = 1._01， _y_1000 _≈ _20000， _w _有一点小小的变化，会对它的输出影响是非常大的。所以 _w _有很大的梯度。有很大的梯度也并没有，把学习率设小一点就好了。但把 _w _设为 0.99，那 _y_1000 _≈ _0。如果把 _w _设为 0.01， _y_1000 _≈ _0。也就是说在 1 的这个地方有很大的梯度，但是在 0.99 这个地方就突然变得非常小，这个时候需要一个很大的学习率。

结论：从这个例子可以看出， RNN 训练的问题其实来自它把同样的东西在转移的时候，在时间按时间的时候，反复使用。所以 _w _只要一有变化，它完全由可能没有造成任何影响，一旦造成影响，影响很大，梯度会很大或很小。所以 **RNN 不好训练的原因不是来自激活函数而是来自于它有时间序列同样的权重在不同的时间点被反复的使用 **

5.7 如何解决 RNN 梯度消失或者爆炸

有什么样的技巧可以解决这个问题呢？广泛被使用的技巧是 LSTM， LSTM 可以让误差表面不要那么崎岖。它会把那些平坦的地方拿掉，解决梯度消失的问题，不会解决梯度爆炸（gradient exploding） 的问题。有些地方还是非常的崎岖的，有些地方仍然是变化非常剧烈的，但是不会有特别平坦的地方。如果做 LSTM 时，大部分地方变化的很剧烈，所以做 LSTM的时候，可以把学习率设置的小一点，保证在学习率很小的情况下进行训练。

Q: 为什么 LSTM 可以解决梯度消失的问题，可以避免梯度特别小呢？为什么把 RNN换成 LSTM？。
A： LSTM 可以处理梯度消失的问题。用这边的式子回答看看。 RNN 跟 LSTM 在面对记忆元的时候，它处理的操作其实是不一样的。在 RNN 里面，在每一个时间点，神经元的输出都要记忆元里面去，记忆元里面的值都是会被覆盖掉。但是在 LSTM 里面不一样，它是把原来记忆元里面的值乘上一个值再把输入的值加起来放到单元里面。所以它的记忆和输入是相加的。 LSTM 和 RNN 不同的是，如果权重可以影响到记忆元里面的值，一旦发生影响会永远都存在。而 RNN 在每个时间点的值都会被格式化掉，所以只要这个影响被格式化掉它就消失了。但是在 LSTM 里面，一旦对记忆元造成影响，影响一直会被留着，除非遗忘门要把记忆元的值洗掉。不然记忆元一旦有改变，只会把新的东西加进来，不会把原来的值洗掉，所以它不会有梯度消失的问题。

遗忘门可能会把记忆元的值洗掉。其实 LSTM 的第一个版本其实就是为了解决梯度消失的问题，所以它是没有遗忘门，遗忘门是后来才加上去的。甚至有个传言是：在训练 LSTM的时候，要给遗忘门特别大的偏置，确保遗忘门在多数的情况下都是开启的，只要少数的情况是关闭的。
有另外一个版本用门操控记忆元，叫做 GRU， LSTM 有三个门，而 GRU 有两个门，所以 GRU 需要的参数是比较少的。因为它需要的参数量比较少，所以它在训练的时候是比较鲁棒的。如果训练 LSTM 的时候，过拟合的情况很严重，可以试下 GRU。 **GRU 的精神就是：旧的不去，新的不来。它会把输入门跟遗忘门联动起来，也就是说当输入门打开的时候，遗忘门会自动的关闭 (格式化存在记忆元里面的值)，当遗忘门没有要格式化里面的值，输入门就会被关起来。也就是要把记忆元里面的值清掉，才能把新的值放进来。 **

5.8 RNN 其他应用

槽填充的例子中假设输入跟输出的数量是一样的，也就是说输入有几个单词，我们就给每一个单词槽标签， RNN 可以做到更复杂的事情。

5.8.1 多对一序列

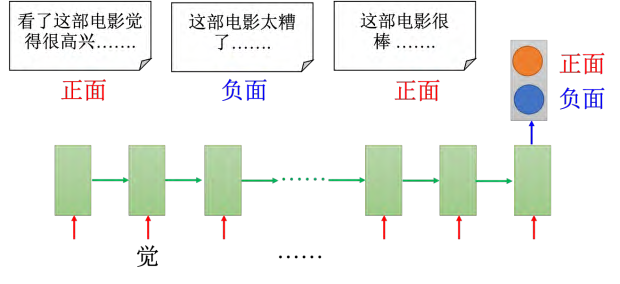
比如输入是一个序列，输出是一个向量。 **情感分析（sentiment analysis） 是典型的应用，如图 5.33 所示，某家公司想要知道，他们的产品在网上的评价是正面的还是负面的。他们可能会写一个爬虫，把跟他们产品有关的文章都爬下来。那这一篇一篇的看太累了，所以可以用一个机器学习的方法学习一个分类器（classifier） **来判断文档的正、负面。或者在电影上，情感分析就是给机器看很多的文章，机器要自动判断哪些文章是正类，哪些文章是负类。

情感分析是一个分类问题，但是因为输入是序列，所以用 RNN 来处理。

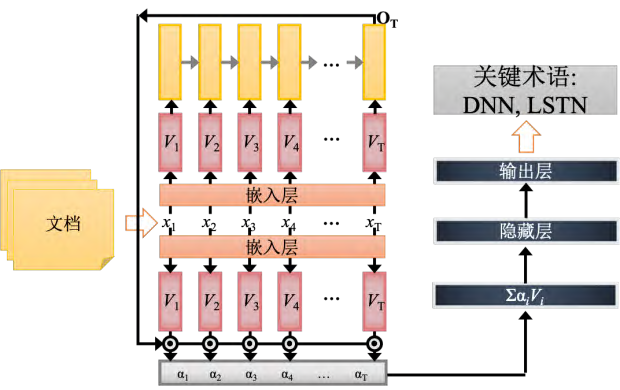
用 RNN 来作关键术语抽取（key term extraction）。关键术语抽取意思就是说给机器看一个文章，机器要预测出这篇文章有哪些关键单词。

5.8.2 多对多序列

通常情况下，输入的是声音序列，输出的是字符序列。然而，由于输出序列比输入序列短，因此无法完全匹配每个向量与对应的字符。为了克服这个问题，一种技巧称为修剪，即将重复的字符删除，以便更好地匹配输入和输出序列。此外，还有一种技巧称为填充（总称CTC），即在输出序列中添加特殊符号，以便更好地处理叠字问题。在训练过程中，需要穷举所有可能的对齐方式，以便让机器学习如何正确地匹配输入和输出序列。最终，机器可以通过训练数据学会如何正确地识别语音并将其转换成文字。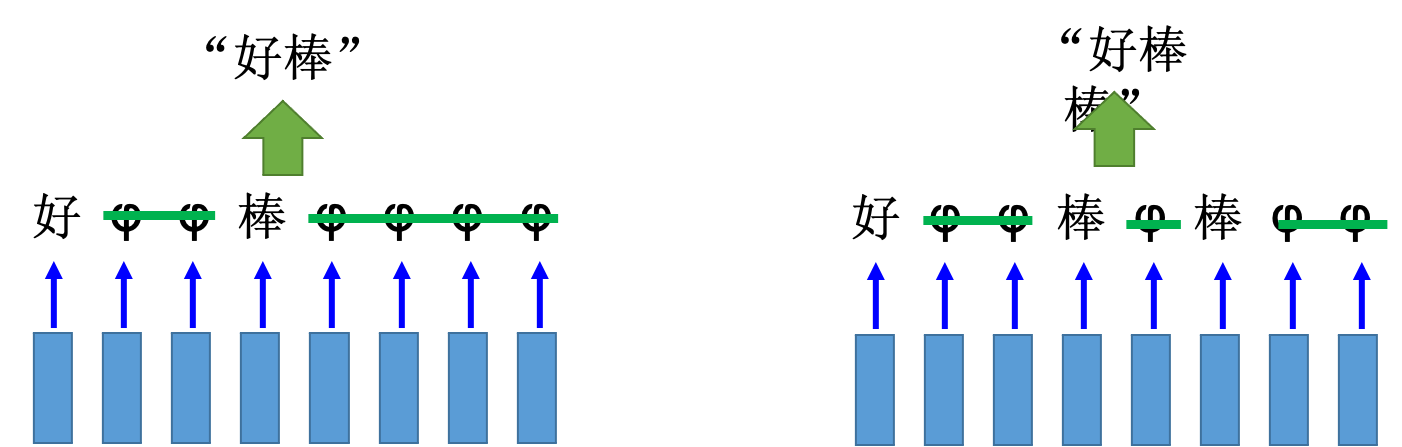

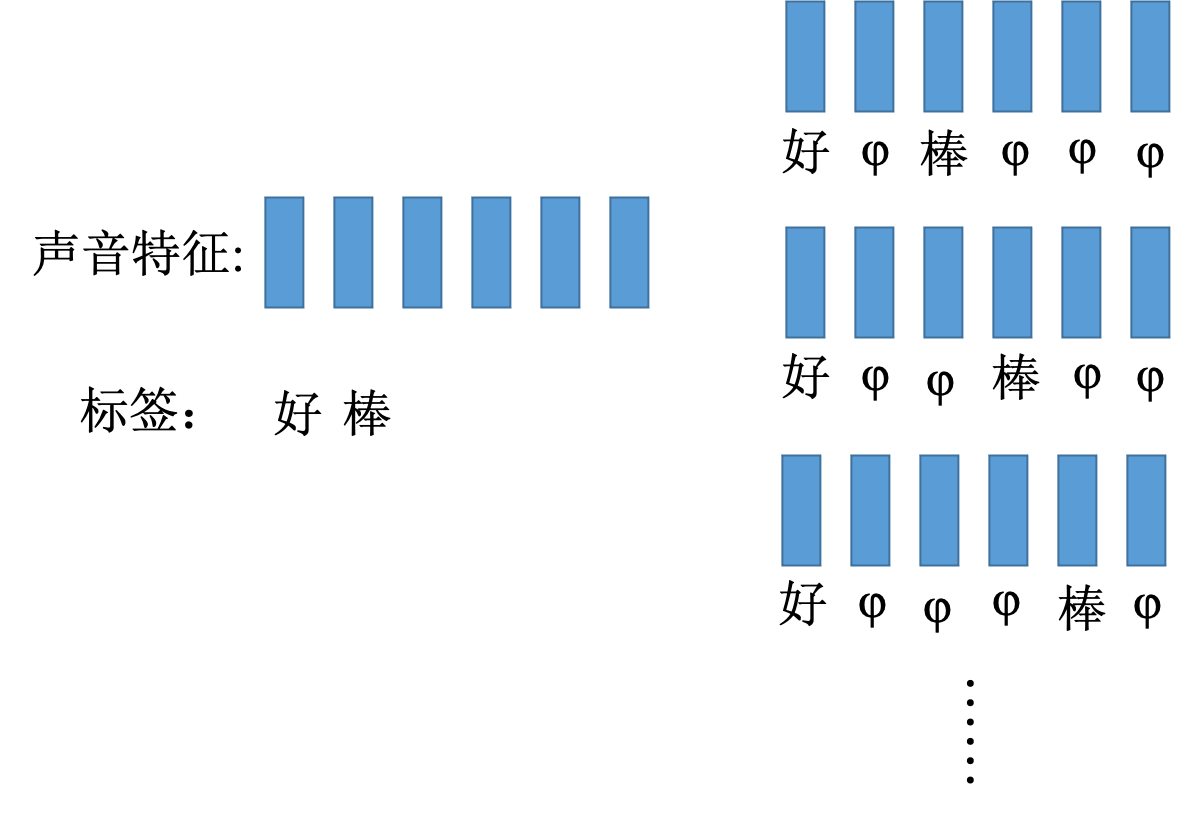
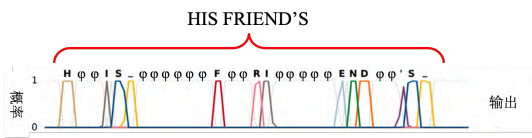
5.8.3 序列到序列

序列到序列的学习应用，其中输入和输出都是序列，但长度不一定相同。例如机器翻译，将英文单词序列翻译成中文字符序列。
要怎么阻止让它产生单词呢？要多加一个符号“断”，所以机器的输出不是只有字符，它还有一个可能输出“断”。如果“习”后面是符号“===”（断）的话，就停下来了

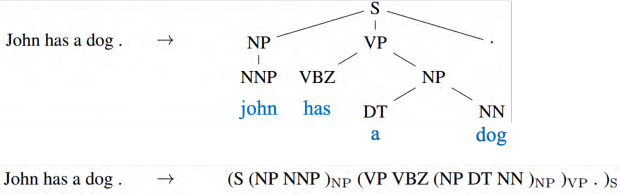
序列到序列的技术也被用到句法解析（syntactic parsing）。句法解析，让机器看一个句子，得到句子结构树。如图 5.42 所示，只要把树状图描述成一个序列，比如：“John has a dog.”，序列到序列学习直接学习一个序列到序列模型，其输出直接就是句法解析树，这个是可以训练的起来的。 LSTM 的输出的序列也是符合文法结构，左、右括号都有。

要将一个文档表示成一个向量，如图 5.43 所示，往往会用 词袋（Bag-of-Words， BoW） 的方法，用这个方法的时候，往往会忽略掉单词顺序信息。举例来说，有一个单词序列是“white blood cells destroying an infection”，另外一个单词序列是：“an infection destroying white blood cells”，这两句话的意思完全是相反的。但是我们用词袋的方法来描述的话，他们的词袋完全是一样的。它们里面有完全一摸一样的六个单词，因为单词的顺序是不一样的，所以他们的意思一个变成正面的，一个变成负面的，他们的意思是很不一样的。可以用序列到序列自编码器这种做法来考虑单词序列顺序的情况下，把一个文档变成一个向量。

我们以后还会对这些进一步深入，感谢您的观看。