神仙公司名单（北京）

神仙公司（北京）

接着奏乐接着舞，神仙公司系列。

这次写之前几期评论区呼声极高的城市：北京。

北京，是许多人外出打工的梦想之都，是年轻人逃离农村的终点站。

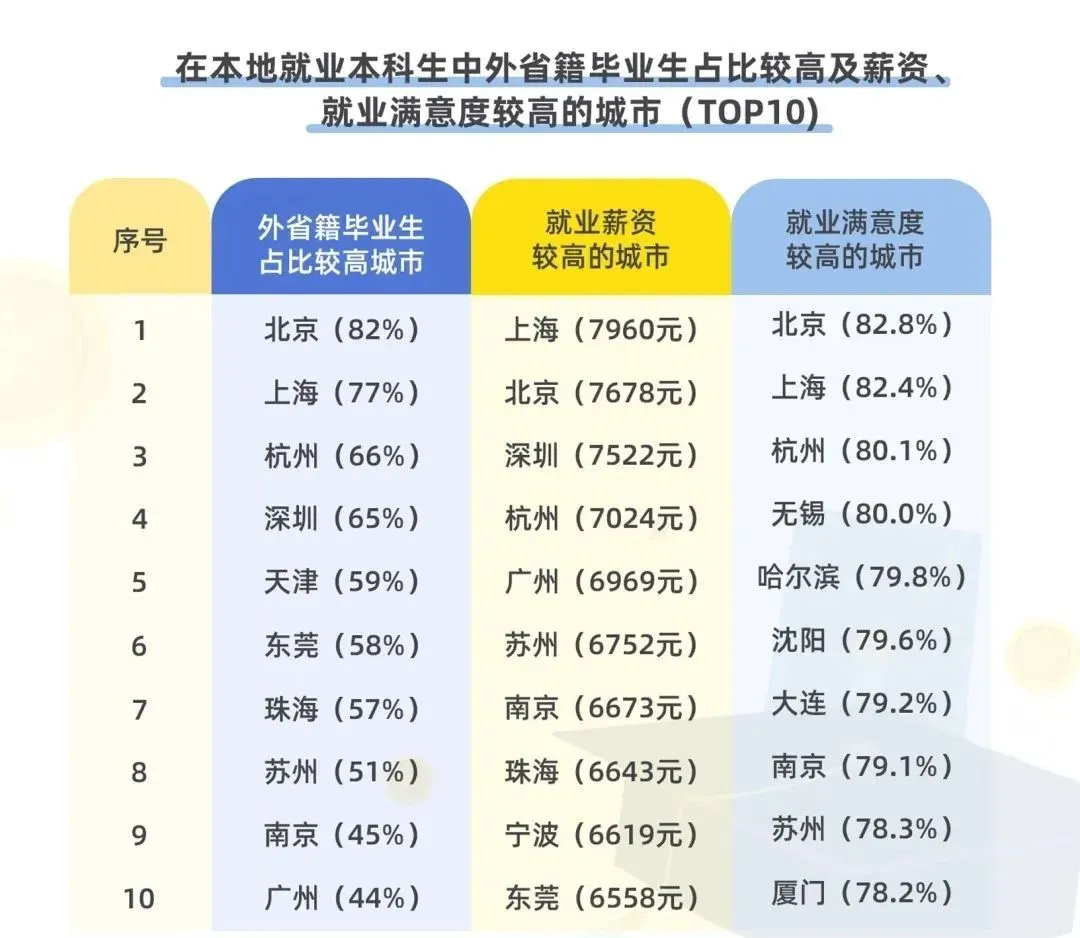
在近两年的就业蓝皮书「外省籍毕业生占比较高城市」、「就业薪资较高的城市」和「就业满意度较高的城市」几项指标中，北京两项排名第一，一项排名第二，综合排名在所有城市中位列第一：

神仙公司不多，HC 通常也有限，因此，除了分享一些毫无争议的神仙公司以外，还会把一些相对较好的"半仙"公司也分享给大家。

一直很稳的 WLB 典范（神仙公司）：

长亭科技：信息安全公司，955，弹性工作，不打卡，包中午和晚餐，饭菜不重样，零食和饮料随便挑，20k~40k，14 薪；
绿盟科技：信息安全上市公司，早9:00晚5:30，五险一金，补充医疗报销，餐补，交通补，节日福利，股票期权，薪资水平 17k~35k，14薪~18薪；
Keep：上市公司，国内健身类 App 绝对头部，弹性工作，不打卡，不加班，双休，办公环境一流，免费健身课程丰富多样，员工活动很多，还有机会见到明星，薪资水平 20k~60k，14 薪；
FreeWheel：965，六险一金，自助午餐，入职即有 15 天年假，定期普调，薪资水平 25k~65k，14 薪；
知乎：上市公司，早10晚7，双休，五险一金，补充医疗保险，节日福利，包吃，零食下午茶，股票期权，薪资水平 14k~40k，15 薪；
彩云天气：国内天气类 App 头部，早10:30晚7:30，弹性工作制，五险一金，补充医疗保险，包吃，零食下午茶，节日福利，加班补助，项目奖金，团队奖金，定期普调，员工旅游和每年体检，薪资水平 15k~35k，15 薪；

还算不错的企业（半仙公司）：

Qualcomm（高通）：世界 500 强，弹性工作制，可远程办公，入职 15 天年假 + 30 天带薪病假，20k~50k，13薪~15薪；
Cisco（思科）：老牌外企，适合养老，女性友好，节日福利，额外补充商业保险，薪资还行，胜在稳定；
豆瓣：日常任务简单轻松，工作氛围轻松愉快，工作薪资水平一般；

以上就是坐标「北京」，目前均有计算机相关在招岗位的神仙公司。

关于「北京」以及「北京神仙公司」，你有什么想分享的呢，欢迎评论区留言。

...

回归主线。

周末，继续开心小算法。

题目描述

平台：LeetCode

题号：81

已知存在一个按非降序排列的整数数组 nums，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（）上进行了旋转，使数组变为（下标从 0 开始计数）。

例如，在下标 5 处经旋转后可能变为。

给你旋转后的数组 nums 和一个整数 target，请你编写一个函数来判断给定的目标值是否存在于数组中。

如果 nums 中存在这个目标值 target，则返回 true，否则返回 false。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0

输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3

输出：false

提示：

题目数据保证 nums 在预先未知的某个下标上进行了旋转

二分

根据题意，我们知道，所谓的旋转其实就是「将某个下标前面的所有数整体移到后面，使得数组从整体有序变为分段有序」。

但和 33. 搜索旋转排序数组不同的是，本题元素并不唯一。

这意味着我们无法直接根据与的大小关系，将数组划分为两段，即无法通过「二分」来找到旋转点。

「因为「二分」的本质是二段性，并非单调性。只要一段满足某个性质，另外一段不满足某个性质，就可以用「二分」。」

如果你有看过我严格 O(logN)，一起看清二分的本质这篇题解，你应该很容易就理解上句话的意思。如果没有也没关系，我们可以先解决本题，在理解后你再去做 33. 搜索旋转排序数组，我认为这两题都是一样的，不存在先后关系。

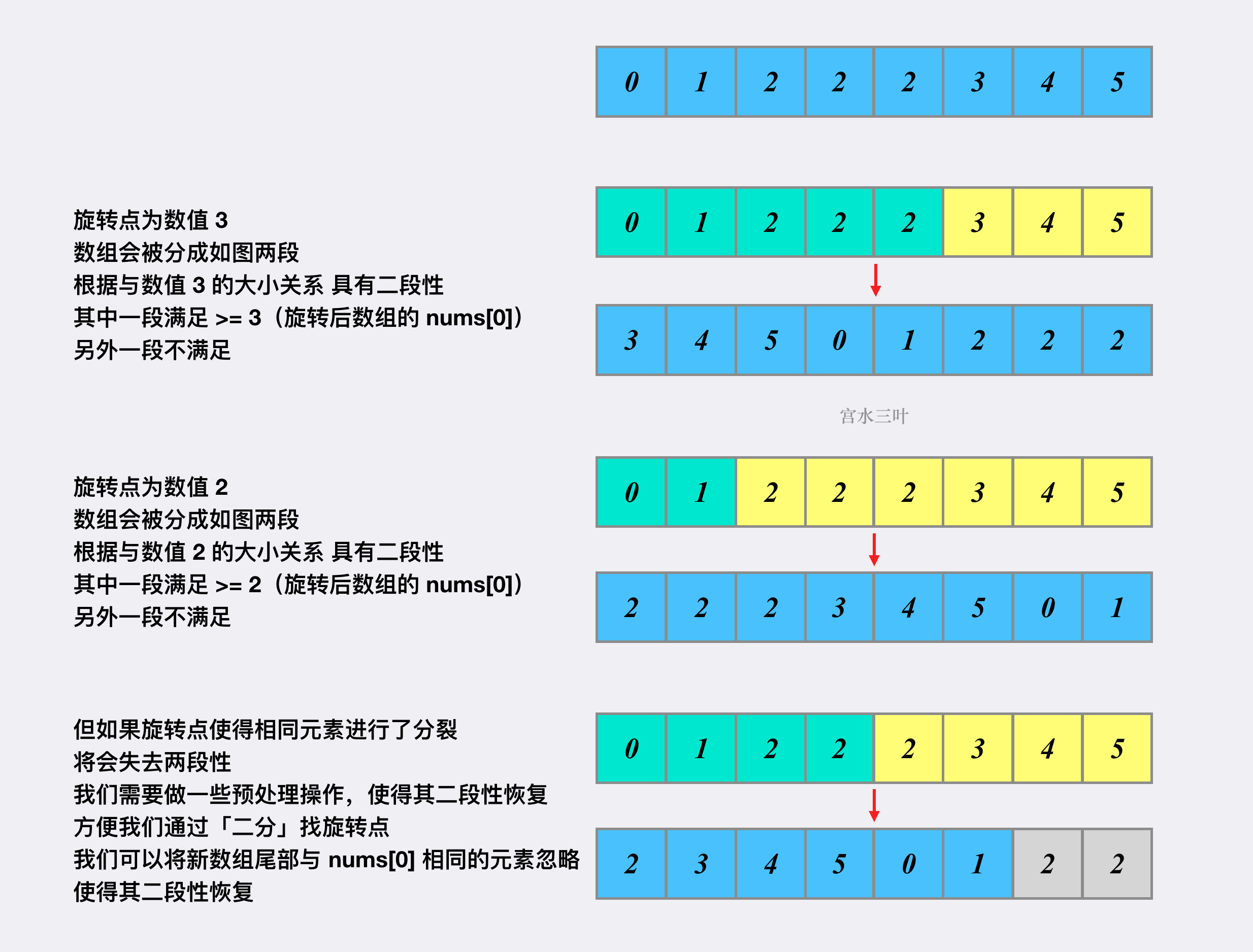
举个🌰，我们使用数据 [0,1,2,2,2,3,4,5] 来理解为什么不同的旋转点会导致「二段性丢失」：

Java 代码：

class Solution {
    public boolean search(int[] nums, int t) {
        int n = nums.length;
        int l = 0, r = n - 1;
        // 恢复二段性
        while (l < r && nums[0] == nums[r]) r--;

        // 第一次二分，找旋转点
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (nums[mid] >= nums[0]) l = mid;    
            else r = mid - 1;
        }
        
        int idx = n;
        if (nums[r] >= nums[0] && r + 1 < n) idx = r + 1;

        // 第二次二分，找目标值
        int ans = find(nums, 0, idx - 1, t);
        if (ans != -1) return true;
        ans = find(nums, idx, n - 1, t);
        return ans != -1;
    }
    int find(int[] nums, int l, int r, int t) {
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= t) r = mid;
            else l = mid + 1;
        }
        return nums[r] == t ? r : -1;
    }
}

C++ 代码：

class Solution {
public:
    bool search(vector<int>& nums, int t) {
        int n = nums.size();
        int l = 0, r = n - 1;
        // 恢复二段性
        while (l < r && nums[0] == nums[r]) r--;

        // 第一次二分，找旋转点
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (nums[mid] >= nums[0]) l = mid;    
            else r = mid - 1;
        }
        int idx = n;
        if (nums[r] >= nums[0] && r + 1 < n) idx = r + 1;

        // 第二次二分，找目标值
        int ans = find(nums, 0, idx - 1, t);
        if (ans != -1) return true;
        ans = find(nums, idx, n - 1, t);
        return ans != -1;
    }
    int find(vector<int>& nums, int l, int r, int t) {
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= t) r = mid;    
            else l = mid + 1;
        }
        return nums[r] == t ? r : -1;
    }
};

Python 代码：

class Solution:
    def search(self, nums: List[int], t: int) -> bool:
        n = len(nums)
        l, r = 0, n - 1
        # 恢复二段性
        while l < r and nums[0] == nums[r]:
            r -= 1

        # 第一次二分，找旋转点
        while l < r:
            mid = l + r + 1 >> 1
            if nums[mid] >= nums[0]: l = mid
            else: r = mid - 1
        
        idx = n
        if nums[r] >= nums[0] and r + 1 < n:
            idx = r + 1

        # 第二次二分，找目标值
        ans = self.find(nums, 0, idx - 1, t)
        if ans != -1: return True
        ans = self.find(nums, idx, n - 1, t)
        return ans != -1

    def find(self, nums, l, r, t):
        while l < r:
            mid = l + r >> 1
            if nums[mid] >= t: r = mid
            else: l = mid + 1
        return r if nums[r] == t else -1

TypeScript 代码：

function find(nums: number[], l: number, r: number, t: number): number {
    while (l < r) {
        const mid: number = l + r >> 1;
        if (nums[mid] >= t) r = mid;
        else l = mid + 1;
    }
    return nums[r] === t ? r : -1;
}
function search(nums: number[], t: number): boolean {
    const n: number = nums.length;
    let l: number = 0, r: number = n - 1;
    // 恢复二段性
    while (l < r && nums[0] === nums[r]) r--;

    // 第一次二分，找旋转点
    while (l < r) {
        const mid: number = l + r + 1 >> 1;
        if (nums[mid] >= nums[0]) l = mid;    
        else r = mid - 1;
    }
    
    let idx: number = n;
    if (nums[r] >= nums[0] && r + 1 < n) idx = r + 1;

    // 第二次二分，找目标值
    const ans: number = find(nums, 0, idx - 1, t);
    if (ans !== -1) return true;
    return find(nums, idx, n - 1, t) !== -1;
};