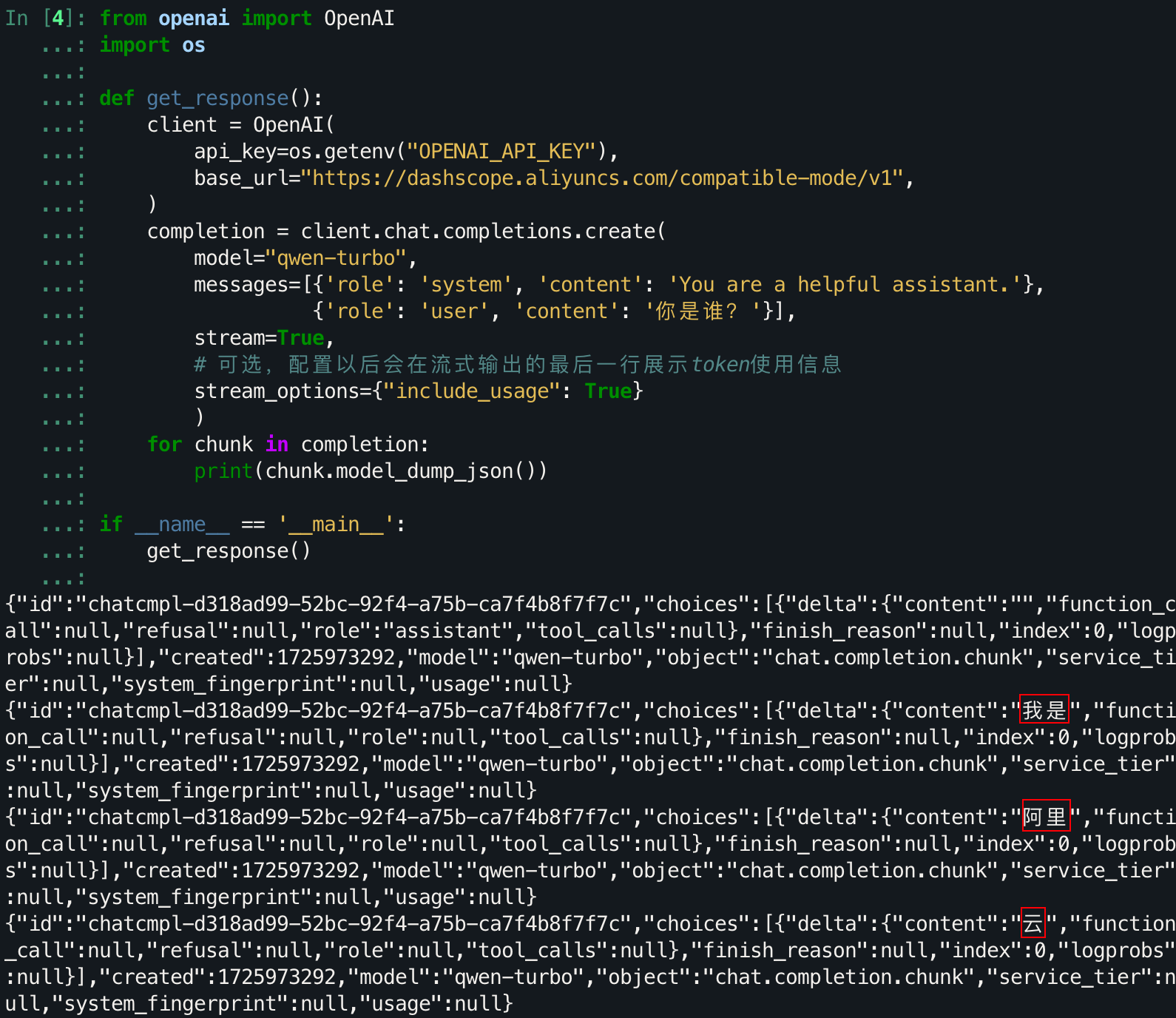
模型诊断元学习（model-agnosticmeta-learning，MAML）， 另一个是Reptile。这两个算法都是在 2017 年提出来的，而且都是基于梯度下降法进行优化 的。那我们最常用的学习算法是梯度下降，在梯度下降中，我们要有一个网络架构，同时初始 化一下这个网络的参数θ0。我们也有一些训练数据，他们是从训练数据里面采样一个批次出 来，然后用这个批次来计算梯度，并用这个梯度来更新参数，从θ0到θ‘，接着再重新计算一 次梯度，再更新参数，就反复这样下去，直到次数够多，输出一个满意的θ∗出来。

        初始化的参数θ0 可以训练的，一般θ0 是随机初始化的，也就是从某一个固定的分布里 面采样出来的。同时θ0 对结果往往有一定程度的影响，好的初始化参数不好的初始化参数可 以天差地远，那我们能不能够透过一些训练的任务，来找出一个对训练特别有帮助的初始化参数呢？这个方法是模型诊断元学习。

        MAML 的基本思路是，算法要最大化模型对超参数的敏感性。也就是说，要让学习到的 超参数让模型的损失函数因为样本的微小变化而有较大的优化。因此，模型的超参数设置应 该能够让损失函数变化的速度最快，即损失函数此时有最大的梯度。因此，损失函数被定义 为每一个任务下该模型的损失函数的梯度的和。剩下要做的，就是根据这个定义的损失函数， 用梯度下降法进行求解。在训练的过程中算法会求取以下两次梯度。第一次求梯度：针对每个 任务，计算损失函数的梯度，进行梯度下降；第二次求梯度：对梯度下降后的参数求和，再求 梯度，进行梯度下降。当然，MAML有另外的变形就叫做Reptile，翻译过来叫爬虫，大家可 以自行了解。需要补充的是，虽然在MAML中，我们要去学习初始化参数的过程，但是在其 中我们也是有很多超参数需要自己决定的。

        这里做一个联想，我们在介绍自监督学习的时候，我们也有提到好的初始化参数的重要 性。在自监督学习中，我们就是有很多的没有标记的数据，可以用一些代理的任务去训练它， 比如说在Bert 里面就是用填空题来训练模型，在图像上也可以做自监督学习。比如把图片的 其中一块盖起来，让机器预测被盖起来的一块是什么东西，机器就可以从中学到一些特征，然 后再把这些特征用在其他的任务上。当然，现在在做图像的自监督学习的时候，可能这个掩码 的方法以及所谓的填空的方法不是最常用的，目前比较流行用对比学习的方法。总之，在自监 督学习中我们会先拿一大些的数据去做预训练，那预训练的结果我们也说它是好的初始化参 数，然后再把这些好的初始化参数用在测试的任务上。

        那这MAML和自监督学习有什么不同呢？其实它们的目的都是一样的，都是要找到好的 初始化参数，但是它们的方法不一样。自监督学习是用一大些的数据去做预训练，而MAML 是用一大些的任务去做预训练。另外过去在自监督学习还没有兴起的时候，也有一些方法是 用一大些的任务去做预训练，这个方法叫做多任务学习。具体来讲，我们一样有好几个任务的 数据，并且把这些好几个任务的数据通通放在一起，然后接下来我们同样可以找到一个好的 初始化参数，然后再把这个好的初始化参数用在测试的任务上，这就是多任务学习。现在我 们在做有关MAML研究的时候，通常会把这种多任务学习的训练方法来当做元学习的基线。 因为这两个方法他们用的数据都是一样的，一边只是我们会把不同的任务分开，另外一边把 所有的任务的数据倒在一起。

        其实MAML 很像是域适应或者迁移学习，也就是我们在某些任务上面学到的东西可以 被被迁移到另外一个域，我们可以说他们是基于分类问题的域适应或者迁移学习。所以我们 在研读文献的时候其实也不用太拘泥于这些词汇，我们要真正要在意的是这些词汇背后所代 表的含义是什么。

        我们下面解释一下MAML的优势。首先有两个假设，第一个假设是MAML找到的初始 参数是一个很厉害的初始参数。它可以让我们的例如梯度下降这种学习算法快速找到每一个 任务的参数。另外一个假设是这个初始化的参数它本来就和每一个任务上最终好的结果已经 非常接近了，所以我们直接应用很少几次的梯度下降就可以轻易的找到好的结果，这个也是 使得MAML有效的关键。当然MAML也有一些变形，比如ANIL（almostnoinner loop）、 First order MAML（FOMAML）以及 Reptile 等等，这里我们不做扩展。

        除了可以学习初始化的参数外，MAML还可以学习优化器，如图1所示。我们在更新 参数的时候，需要决定比如说学习率、动量等等的参数。像学习率这种超参数进行自动更新 的方法在很早以前就有了，NIPS2016 年就有一篇文章，叫做“Learning to learn by gradient descent by gradient descent”。在这篇文章里面呢，作者直接学习了优化器，一般我们的优化器都是人为规定的（比如ADAM等等），而这个文章中的参数是根据训练的任务自动学出来 的。

图1 MAML 中可学习的优化器

        当然我们还可以训练网络架构，这部分的研究被称为神经网络架构搜索（NeuralArchi tecture Search，NAS）。如果在元学习中我们学习的是网络的架构，讲网络架构当作ϕ的 话，那我们就是在做NAS。在NAS里面，ϕ是网络架构，我们要找一个ϕ去最小化L(ϕ)。 这其中我们做L(ϕ)的微分就有可能出问题了。当我们遇到优化问题时并且没办法上微分的时 候，强化学习也许是一个解决方法。具体做法是，我们可以把ϕ想成是一个智能体的参数，这 个智能体的输出是NAS中相关的超参数。举例来说，现在第一层的滤波器它的长是多少，宽 是多少，步长是多少，数目是多少等等。我们智能体的输出就是NAS中相关的参数，然后接 下来我们要训练智能体，让它去最大化一个回报，即−L(ϕ)，让他去最大化这个回报，就等 于最小化L(ϕ)，也就是我们要找的最优的ϕ。

        下面是从一篇文章中截取的一个NAS的例子，以此为例介绍NAS的过程，如图2所 示。具体来讲，我们有一个智能体是RNN架构。这个RNN架构每次会输出一个网络架构有 关的参数，比如它会输出滤波器的高是多少，再输出过滤器的宽是多少，接着再输出步长是 多少等等。第一层第二层输出完了以后，接下来输出n+1层，再输出n+2层，以此类推。有 了这些参数以后，就根据它们设计一个网络以后就去训练这个网络，这个过程其实就是之前 我们介绍的单一任务训练。然后接下来就去做强化学习，我们可以把这一个网络他在测试数 据上面的准确率当做回报来训练智能体，目标是最大化回报，这个过程其实就是跨任务训练。 那除了强化学习以外，其实用演变算法也是可以的。本质上其实就是硬要把网络架构改一下， 让它变得可以微分。其中有一个经典的做法叫做可微分架构搜索，这个方法的本质就是想办 法让问题变的是可以微分，从而可以直接用梯度下降来最小化这个损失函数。

        除了网络架构可以学习外，其实数据处理部分也有可能可以学习。我们在训练网络的时 候，通常要做数据增强。那在元学习中我们可以让机器自动进行数据增强。另一个角度，我们 在训练的时候，有时候会需要给不同样本不同的权重。具体操作的话就会有不同的策略，比如 有的策略就是如果有一些样例距离分类边界线特别近，那说明其很难被分类，这样类似的样 例也许就要给它们比较大的权重，这样网络就会聚焦在这些比较难分别的样例中，希望它们可以被学得比较好。但是也有文献有相反的结论，比如比较有干扰噪声的这些样本应该给它 比较小的权重，这些样例如果比较接近分类边界线，可能代表它比较有噪声干扰，代表它可能 标签本身就标错了，或者分类是不合理的等等，也许就应该给这些样本比较小的权重。那元学 习中如何决定这个采样权重的策略呢？我们可以用学习的方式把采样策略直接学出来，然后 根据采样数据的特性自动决定采样数据的权重如何设计。

图2 NAS 的实例

        到目前为止，我们看到的这些方法都是基于梯度下降再去做改进的，我们有没有可能完 全舍弃掉梯度下降呢？比如，我们有没有可能直接学习一个网络，这个网络的参数ϕ，网络直 接训练数据作为输入直接输出训练好的结果？如果真的有这样一个网络，它可以将训练数据 作为输入输出训练好的网络的参数，那我们就可以让机器发明了新的学习算法。这个是有可 能的，并且已经有了一些论文。不过到目前为止，我们还是把训练跟测试分成两个阶段，我们 有一个学习算法使用训练数据进行训练，然后输出训练好的结果，并把训练好的结果用在测 试数据上。我们想看看有没有可能更进一步，直接把整个回合，也就是一次训练加一次测试合 并在一起。有一些工作，它就是直接把训练数据和测试数据当做网络的输入，网络输入完训 练数据以后，机器也许学出了一个学习算法，也许找出一组参数等等，再它输入训练数据以 后再给他测试数据，它就可以直接输出这些测试数据的答案。这个时候我们不再有训练和测 试的分界，在一个回合里面不再分训练和测试，而是直接用个网络把训练和测试这件事情一 次搞定。目前这种系列的方法叫做“learning to compare”，它又叫做基于度量的方法，这一系 列的做法就可以看作是训练和测试没有分界，一个网络直接把训练数据和测试数据都读进去， 而直接输出测试数据的结果。