322. 零钱兑换
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
力扣题目链接(opens new window)
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
- 输入:coins = [1, 2, 5], amount = 11
- 输出:3
- 解释:11 = 5 + 5 + 1
示例 2:
- 输入:coins = [2], amount = 3
- 输出:-1
示例 3:
- 输入:coins = [1], amount = 0
- 输出:0
示例 4:
- 输入:coins = [1], amount = 1
- 输出:1
示例 5:
- 输入:coins = [1], amount = 2
- 输出:2
提示:
- 1 <= coins.length <= 12
- 1 <= coins[i] <= 2^31 - 1
- 0 <= amount <= 10^4
在 518.零钱兑换Ⅱ 中我们已经兑换一次零钱了,这次又要兑换,套路不一样!
题目中说每种硬币的数量是无限的,可以看出是典型的完全背包问题。
动规五部曲分析如下:
-
确定dp数组以及下标的含义
dp[j]:凑足总额为 j 所需钱币的最少个数为dp[j]
-
确定递推公式
凑足总额为 j - coins[i] 的最少个数为 dp[j - coins[i]] ,那么只需要加上一个钱币 coins[i] 即 dp[j - coins[i]] + 1 就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
-
dp数组如何初始化
首先凑足总金额为 0 所需钱币的个数一定是 0 ,那么 dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j] 必须初始化为一个最大的数,否则就会在 min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非 0 的元素都是应该是最大值。
代码如下:
int[] dp = new int[amount + 1];
Arrays.fill(dp, INT_MAX);
dp[0] = 0;
-
确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
所以本题的两个for循环的关系是:外层for循环遍历物品,内层for遍历背包或者外层for遍历背包,内层for循环遍历物品都是可以的!
那么下面采用coins放在外循环,target在内循环的方式。
本题钱币数量可以无限使用,那么是完全背包。所以遍历的内循环是正序
综上所述,遍历顺序为:coins(物品)放在外循环,target(背包)在内循环。且内循环正序。
-
举例推导dp数组
以输入:coins = [1, 2, 5], amount = 5为例
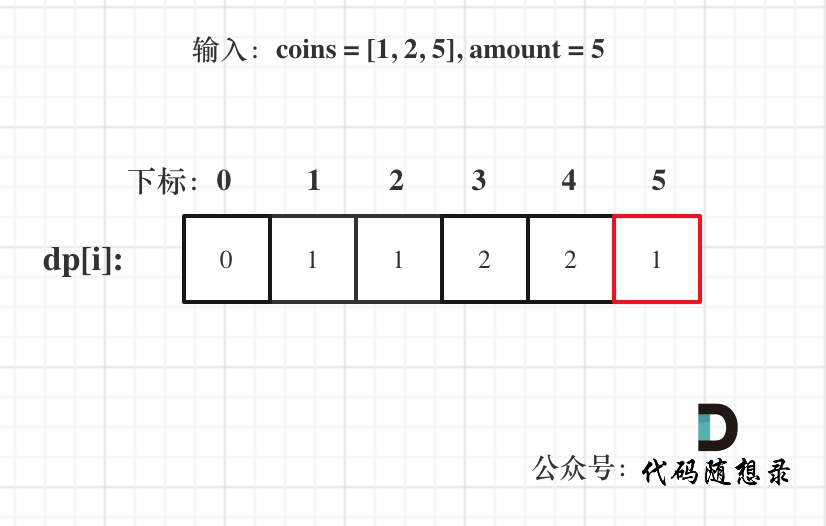
dp[amount]为最终结果。
以上分析完毕,Java代码如下:
class Solution {public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];//初始化dp数组为最大值for (int j = 0; j < dp.length; j++) {dp[j] = max;}//当金额为0时需要的硬币数目为0dp[0] = 0;for (int i = 0; i < coins.length; i++) {//正序遍历:完全背包每个硬币可以选择多次for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != max) {//选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];}
}- 时间复杂度: O(n * amount),其中 n 为 coins 的长度
- 空间复杂度: O(amount)
总结
细心的同学看网上的题解,可能看一篇是遍历背包的for循环放外面,看一篇又是遍历背包的for循环放里面,看多了都看晕了,到底两个for循环应该是什么先后关系。
这也是学习动态规划的苦恼所在,有的时候递推公式很简单,难在遍历顺序上!
但最终又可以稀里糊涂的把题目过了,也不知道为什么这样可以过,反正就是过了。
本题是要求最少硬币数量,硬币是组合数还是排列数都无所谓!所以两个for循环先后顺序怎样都可以!
279.完全平方数
本题 和 322. 零钱兑换 基本是一样的,大家先自己尝试做一做
力扣题目链接(opens new window)
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
- 输入:n = 12
- 输出:3
- 解释:12 = 4 + 4 + 4
示例 2:
- 输入:n = 13
- 输出:2
- 解释:13 = 4 + 9
提示:
- 1 <= n <= 10^4
可能刚看这种题感觉没啥思路,又平方和的,又最小数的。
我来把题目翻译一下:完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
感受出来了没,这么浓厚的完全背包氛围,而且和上一题就是一模一样的
老规矩动规五部曲分析如下:
-
确定dp数组(dp table)以及下标的含义
dp[j]:和为 j 的完全平方数的最少数量为 dp[j]
-
确定递推公式
dp[j] 可以由 dp[j - i * i] 推出, dp[j - i * i] + 1 便可以凑成 dp[j]。
此时我们要选择最小的 dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
-
dp数组如何初始化
dp[0] 表示和为 0 的完全平方数的最小数量,那么dp[0]一定是0。
有同学问题,那0 * 0 也算是一种啊,为啥dp[0] 就是 0呢?
看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, ...),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。
非0下标的 dp[j] 应该是多少呢?
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
-
确定遍历顺序
我们知道这是完全背包,
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
所以本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
我这里给出外层遍历背包,内层遍历物品的代码:
int[] dp = new int[n + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int i = 0; i <= n; i++) { // 遍历背包for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i - j * j] + 1, dp[i]);}
}-
举例推导dp数组
已输入n为5例,dp状态图如下:

dp[0] = 0 dp[1] = min(dp[0] + 1) = 1 dp[2] = min(dp[1] + 1) = 2 dp[3] = min(dp[2] + 1) = 3 dp[4] = min(dp[3] + 1, dp[0] + 1) = 1 dp[5] = min(dp[4] + 1, dp[1] + 1) = 2
最后的dp[n]为最终结果。
以上动规五部曲分析完毕,Java代码如下:
class Solution {// 版本一,先遍历物品, 再遍历背包public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];//初始化for (int j = 0; j <= n; j++) {dp[j] = max;}//如果不想要寫for-loop填充數組的話,也可以用JAVA內建的Arrays.fill()函數。//Arrays.fill(dp, Integer.MAX_VALUE);//当和为0时,组合的个数为0dp[0] = 0;// 遍历物品for (int i = 1; i * i <= n; i++) {// 遍历背包for (int j = i * i; j <= n; j++) {//if (dp[j - i * i] != max) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);//}//不需要這個if statement,因爲在完全平方數這一題不會有"湊不成"的狀況發生( 一定可以用"1"來組成任何一個n),故comment掉這個if statement。}}return dp[n];}
}class Solution {// 版本二, 先遍历背包, 再遍历物品public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];// 初始化for (int j = 0; j <= n; j++) {dp[j] = max;}// 当和为0时,组合的个数为0dp[0] = 0;// 遍历背包for (int j = 1; j <= n; j++) {// 遍历物品for (int i = 1; i * i <= j; i++) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
}- 时间复杂度: O(n * √n)
- 空间复杂度: O(n)
139.单词拆分
力扣题目链接(opens new window)
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
- 输入: s = "leetcode", wordDict = ["leet", "code"]
- 输出: true
- 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2:
- 输入: s = "applepenapple", wordDict = ["apple", "pen"]
- 输出: true
- 解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
- 注意你可以重复使用字典中的单词。
示例 3:
- 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
- 输出: false
单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。
拆分时可以重复使用字典中的单词,说明就是一个完全背包!
动规五部曲分析如下:
-
确定dp数组以及下标的含义
dp[i] : 字符串长度为 i 的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
-
确定递推公式
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是 true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
-
dp数组如何初始化
从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么 dp[0] 就是递推的根基,dp[0]一定要为true,否则递推下去后面都都是false了。
那么dp[0]有没有意义呢?
dp[0]表示如果字符串为空的话,说明出现在字典里。
但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现 i 为0的情况,那么 dp[0] 初始为true完全就是为了推导公式。
下标非 0 的 dp[i] 初始化为 false,只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。
-
确定遍历顺序
题目中说是拆分为一个或多个在字典中出现的单词,所以这是完全背包。
还要讨论两层for循环的前后顺序。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
本题其实我们求的是排列数,为什么呢。 拿 s = "applepenapple", wordDict = ["apple", "pen"] 举例。
"apple", "pen" 是物品,那么我们要求 物品的组合一定是 "apple" + "pen" + "apple" 才能组成 "applepenapple"。
"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的,那么我们就是强调物品之间顺序。
所以说,本题一定是 先遍历 背包,再遍历物品。
-
举例推导dp[i]
以输入: s = "leetcode", wordDict = ["leet", "code"]为例,dp状态如图:
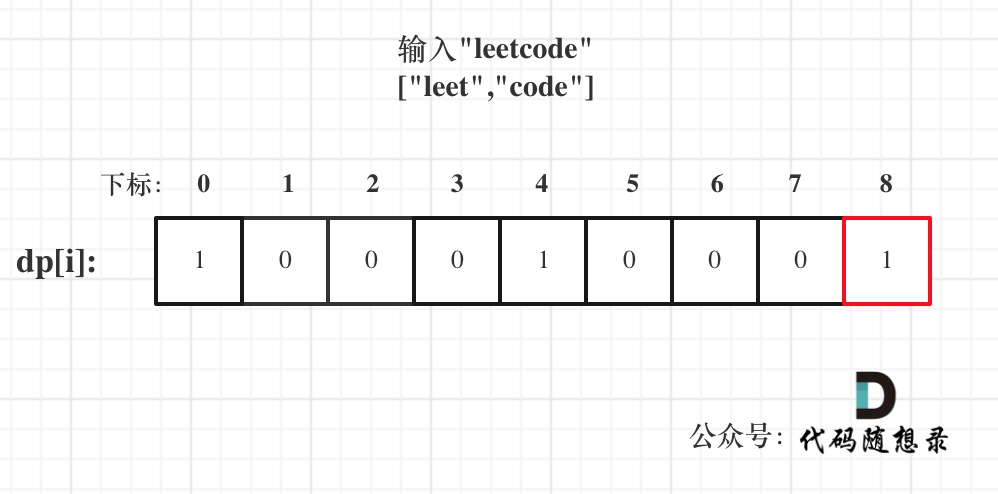
dp[s.length()]就是最终结果。
动规五部曲分析完毕,Java代码如下:
class Solution {public boolean wordBreak(String s, List<String> wordDict) {HashSet<String> set = new HashSet<>(wordDict);boolean[] valid = new boolean[s.length() + 1];valid[0] = true;for (int i = 1; i <= s.length(); i++) {for (int j = 0; j < i && !valid[i]; j++) {if (set.contains(s.substring(j, i)) && valid[j]) {valid[i] = true;}}}return valid[s.length()];}
}- 时间复杂度:O(n^3),因为substr返回子串的副本是O(n)的复杂度(这里的n是substring的长度)
- 空间复杂度:O(n)
关于多重背包
对于多重背包,力扣上还没发现对应的题目,所以这里就做一下简单介绍,大家大概了解一下。
有 N 种物品和一个容量为 V 的背包。第 i 种物品最多有 Mi 件可用,每件耗费的空间是 Ci ,价值是 Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量,且价值总和最大。
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
例如:
背包最大重量为10。
物品为:
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 2 |
| 物品1 | 3 | 20 | 3 |
| 物品2 | 4 | 30 | 2 |
问背包能背的物品最大价值是多少?
和如下情况有区别么?
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 1 |
| 物品0 | 1 | 15 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品2 | 4 | 30 | 1 |
| 物品2 | 4 | 30 | 1 |
毫无区别,这就转成了一个01背包问题了,且每个物品只用一次。
练习题目:卡码网第56题,多重背w包(opens new window)
代码如下:
import java.util.Scanner;
class multi_pack{public static void main(String [] args) {Scanner sc = new Scanner(System.in);/*** bagWeight:背包容量* n:物品种类*/int bagWeight, n;//获取用户输入数据,中间用空格隔开,回车键换行bagWeight = sc.nextInt();n = sc.nextInt();int[] weight = new int[n];int[] value = new int[n];int[] nums = new int[n];for (int i = 0; i < n; i++) weight[i] = sc.nextInt();for (int i = 0; i < n; i++) value[i] = sc.nextInt();for (int i = 0; i < n; i++) nums[i] = sc.nextInt();int[] dp = new int[bagWeight + 1];//先遍历物品再遍历背包,作为01背包处理for (int i = 0; i < n; i++) {for (int j = bagWeight; j >= weight[i]; j--) {//遍历每种物品的个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) {dp[j] = Math.max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}System.out.println(dp[bagWeight]);}
}- 时间复杂度:O(m × n × k),m:物品种类个数,n背包容量,k单类物品数量
从代码里可以看出是01背包里面在加一个for循环遍历一个每种商品的数量。 和01背包还是如出一辙的。
当然还有那种二进制优化的方法,其实就是把每种物品的数量,打包成一个个独立的包。
和以上在循环遍历上有所不同,因为是分拆为各个包最后可以组成一个完整背包,具体原理我就不做过多解释了,大家了解一下就行,面试的话基本不会考完这个深度了,感兴趣可以自己深入研究一波。
总结
多重背包在面试中基本不会出现,力扣上也没有对应的题目,大家对多重背包的掌握程度知道它是一种01背包,并能在01背包的基础上写出对应代码就可以了。
至于背包九讲里面还有混合背包,二维费用背包,分组背包等等这些,大家感兴趣可以自己去学习学习,这里也不做介绍了,面试也不会考。