代码随想录Day 42|leetcode题目：188.买卖股票的最佳时机IV、309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费

提示：DDU，供自己复习使用。欢迎大家前来讨论~

文章目录

  • 题目
    • 题目一：188.买卖股票的最佳时机IV
      • 解题思路：
    • 题目二：309.最佳买卖股票时机含冷冻期
      • 解题思路：
    • 题目三： 714.买卖股票的最佳时机含手续费
      • 解题思路
  • 股票总结

题目

题目一：188.买卖股票的最佳时机IV

[188. 买卖股票的最佳时机 IV](https://leetcode.cn/problems/combinations/)

解题思路：

买卖股票的进阶版，这里要求至多有k次交易。

动规五部曲，分析如下：

  1. 确定dp数组以及下标的含义

在动态规划：123.买卖股票的最佳时机III (opens new window)中，定义了一个二维dp数组，本题其实依然可以用一个二维dp数组。

使用二维数组 dp[i][j] ：第i天的状态为j，所剩下的最大现金是dp[i][j]

j的状态表示为：

  • 0 表示不操作
  • 1 第一次买入
  • 2 第一次卖出
  • 3 第二次买入
  • 4 第二次卖出
  • …

规律: 除了0以外，偶数就是卖出，奇数就是买入。

题目要求是至多有K笔交易，那么j的范围就定义为 2 * k + 1 就可以了。

所以二维dp数组的C++定义为：

vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
  1. 确定递推公式

还要强调一下：dp[i][1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区。

达到dp[i][1]状态，有两个具体操作：

  • 操作一：第i天买入股票了，那么dp[i][1] = dp[i - 1][0] - prices[i]
  • 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]

选最大的，所以 dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);

同理dp[i][2]也有两个操作：

  • 操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
  • 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]

所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])

同理可以类比剩下的状态，代码如下：

for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}

本题和动态规划：123.买卖股票的最佳时机III (opens new window)最大的区别就是这里要类比j为奇数是买，偶数是卖的状态。

  1. dp数组如何初始化

    1. dp[0][0] = 0：第0天没有进行任何操作，收益为0。

    2. dp[0][1] = -prices[0]：第0天进行了第一次买入操作，需要支付购买股票的费用，因此收益为负。

    3. dp[0][2] = 0：第0天进行了第一次卖出操作，当天买入当天卖出，收益为0。

    4. dp[0][3] = -prices[0]：第0天进行了第二次买入操作，需要再次支付购买股票的费用，因此收益为负。

    5. dp[0][4] = 0：第0天进行了第二次卖出操作，由于之前已经卖出过一次，所以这次卖出不会改变收益，收益为0。

对于 dp[0][j] 当 j 为奇数时，都初始化为 -prices[0]，这是因为奇数次交易意味着至少有一次买入操作，而第0天的买入操作会导致收益减少 prices[0]

代码如下：

for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0];
}

在初始化的地方同样要类比j为偶数是卖、奇数是买的状态。

  1. 确定遍历顺序

从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

  1. 举例推导dp数组

以输入[1,2,3,4,5]，k=2为例。

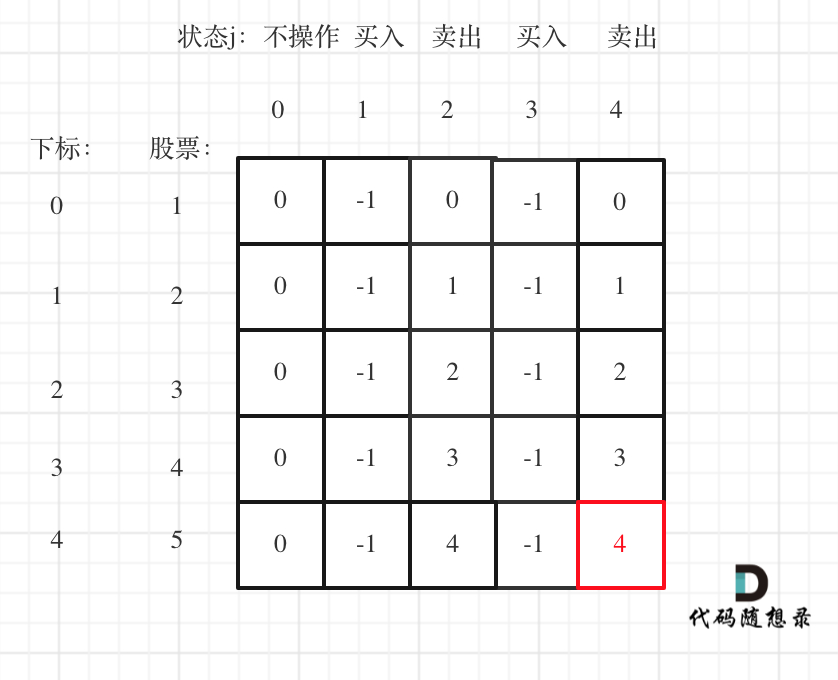
188.买卖股票的最佳时机IV

最后一次卖出，一定是利润最大的，dp[prices.size() - 1][2 * k]即红色部分就是最后求解。

以上分析完毕，C++代码如下：

class Solution {
public:int maxProfit(int k, vector<int>& prices) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0];}for (int i = 1;i < prices.size(); i++) {for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[prices.size() - 1][2 * k];}
};
  • 时间复杂度: O(n * k)，其中 n 为 prices 的长度
  • 空间复杂度: O(n * k)

题目二：309.最佳买卖股票时机含冷冻期

309. 买卖股票的最佳时机含冷冻期

解题思路：

本题加上了一个冷冻期

有两个状态，持有股票后的最多现金，和不持有股票的最多现金。

动规五部曲，分析如下：

  1. 确定dp数组以及下标的含义

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

具体可以区分出如下四个状态：

  • 状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
  • 不持有股票状态，这里就有两种卖出股票状态
    • 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
    • 状态三：今天卖出股票
  • 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

img

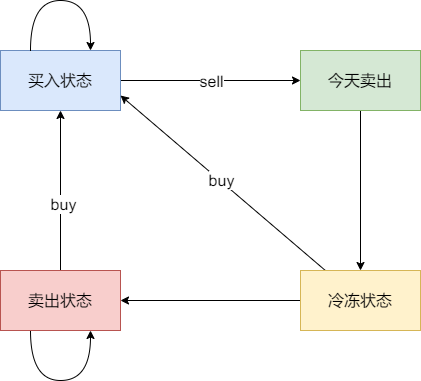
j的状态为：

  • 0：状态一
  • 1：状态二
  • 2：状态三
  • 3：状态四

状态表示的不是某一天的操作，而是到那一天为止的交易状态。这里的状态指的是持有股票的状态，而不是指某一天具体买入股票的操作。

  1. 确定递推公式

达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：

  • 操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
  • 操作二：今天买入了，有两种情况
    • 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
    • 前一天是保持卖出股票的状态（状态二），dp[i - 1][1] - prices[i]

那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);

达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：

  • 操作一：前一天就是状态二
  • 操作二：前一天是冷冻期（状态四）

dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：

昨天一定是持有股票状态（状态一），今天卖出

即：dp[i][2] = dp[i - 1][0] + prices[i];

达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：

昨天卖出了股票（状态三）

dp[i][3] = dp[i - 1][2];

综上分析，递推代码如下：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
  1. dp数组如何初始化

第0天的初始化情况：

持有股票状态（状态一）：dp[0][1] = -prices[0]。这个状态表示在第0天买入了股票，因此持有股票的成本是负的，即 -prices[0]。这里的负号表示你支付了这笔钱。

保持卖出股票状态（状态二）：dp[0][2] = 0。这个状态表示在第0天之前已经卖出了股票，因此不持有股票，收益为0。这个状态是后续可能再次买入股票的前提。

今天卖出了股票（状态三）：dp[0][3] = 0。这个状态表示在第0天卖出了股票，由于是当天卖出，所以收益为0，表示没有额外的收益或损失。

  1. 确定遍历顺序

从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。

  1. 举例推导dp数组

以 [1,2,3,0,2] 为例，dp数组如下：

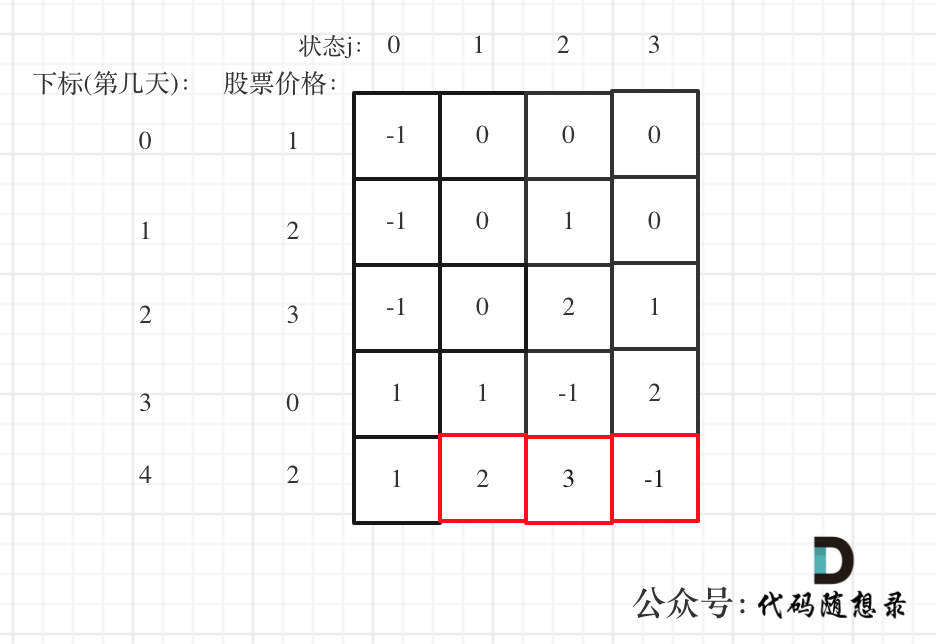
309.最佳买卖股票时机含冷冻期

在计算最多两次交易的最大收益时，最后结果应考虑三种状态：持有股票状态（状态二）、今天卖出股票状态（状态三）和冷冻期状态（状态四），并取这三种状态的最大值作为最终答案。

代码如下：

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();if (n == 0) return 0;vector<vector<int>> dp(n, vector<int>(4, 0));dp[0][0] -= prices[0]; // 持股票for (int i = 1; i < n; i++) {dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);dp[i][2] = dp[i - 1][0] + prices[i];dp[i][3] = dp[i - 1][2];}return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));}
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

题目三： 714.买卖股票的最佳时机含手续费

714. 买卖股票的最佳时机含手续费

解题思路

  1. 贪心算法：
    • 适用于“买卖股票的最佳时机含手续费”问题。
    • 时间复杂度：O(n)，其中n是交易天数。
    • 空间复杂度：O(1)，不需要额外存储空间。
    • 算法理解起来可能有些困难，容易出错。
  2. 动态规划算法：
    • 与“买卖股票的最佳时机II”问题类似，但需要在卖出股票时减去手续费。
    • 动态规划通过维护一个二维数组 dp[i][j] 来解决问题，其中 dp[i][0] 表示第i天持有股票的最大现金，dp[i][1] 表示第i天不持有股票的最大现金。
    • 状态转移方程：
      • dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])：第i天持有股票的状态可以由前一天持有股票或前一天不持有股票并买入股票得到。
      • dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee)：第i天不持有股票的状态可以由前一天不持有股票或前一天持有股票并卖出股票（减去手续费）得到。
    • 与“买卖股票的最佳时机II”的主要区别在于卖出股票时需要减去手续费。

以上分析完毕，C++代码如下：

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2, 0));dp[0][0] -= prices[0]; // 持股票for (int i = 1; i < n; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);}return max(dp[n - 1][0], dp[n - 1][1]);}
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

股票总结

  1. 买卖一次：
    • 最佳时机问题，目的是找到买入和卖出的最佳时间点以获得最大利润。
    • 贪心策略：只需找到价格最低点买入，价格最高点卖出。
  2. 买卖多次：
    • 可以多次买卖，关键是找到所有价格差的最大值。
    • 动态规划或贪心策略：累加所有正的价格差。
  3. 最多买卖两次：
    • 动态规划：维护两个状态，持有股票和不持有股票的最大收益。
    • 关键是找到两次买入和卖出的最佳时机。
  4. 买卖k次：
    • 动态规划：对于每一次交易，都找到买入和卖出的最佳时机。
    • 状态转移复杂，需要考虑所有可能的交易组合。
  5. 冷冻期：
    • 在某些问题中，卖出股票后需要等待一天才能再次买入。
    • 动态规划：在状态转移中添加额外的考虑，确保遵守冷冻期规则。
  6. 手续费：
    • 卖出股票时需要支付手续费。
    • 动态规划：在计算收益时减去手续费。

无论问题如何变化，核心思想是利用动态规划来维护不同状态下的最大收益，并根据问题的具体要求（如买卖次数、冷冻期、手续费等）调整状态转移方程。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/423021.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

摊牌了！一文教会你轻松上手豆包MarsCode 编程助手！

摊牌了！一文教会你轻松上手豆包MarsCode 编程助手！

豆包MarsCode 编程助手是豆包旗下的 AI 编程助手&#xff0c;提供以智能代码补全为代表的 AI 功能。豆包MarsCode 编程助手支持主流的编程语言和 IDE&#xff0c;在开发过程中提供单行代码或整个函数的编写建议。此外&#xff0c;它还支持代码解释、单测生成和问题修复等功能&a…
阅读更多...
有关采用parallelStream并行流处理List并使用自定义线程池和lettuce redis客户端一起使用的问题

有关采用parallelStream并行流处理List并使用自定义线程池和lettuce redis客户端一起使用的问题

在使用parallelStream进行处理list时&#xff0c;如不指定线程池&#xff0c;默认的并行度采用cpu核数进行并行&#xff0c;这里采用ForJoinPool来指定线程池&#xff0c;但循环中使用了luttuce 来获取redis的key时&#xff0c;出现没有控制住线程池的线程数问题。具体上代码。…
阅读更多...
SAP B1 学习笔记 - 易混淆字段名（持续更新中）

SAP B1 学习笔记 - 易混淆字段名（持续更新中）

背景 在 SAP B1 的单据中&#xff0c;由于同一单据时常对应着多个后台表单&#xff0c;且后台表单内包含的字段信息往往远大于单据显示出来的&#xff0c;在配置时经常出现多个字段混淆、无系统信息提示字段名模糊的情况&#xff0c;这里总结常见的易混淆难查找的后台字段名。…
阅读更多...
AIGC6: 走进腾讯数字盛会

AIGC6: 走进腾讯数字盛会

图中是一个程序员&#xff0c;去参加一个技术盛会。AI大潮下&#xff0c;五颜六色&#xff0c;各种不确定。 背景 AI对各行各业的冲击越来越大&#xff0c;身处职场的我也能清晰的感受到。 我所在的行业为全球客服外包行业。 业务模式为&#xff1a; 为国际跨境公司提供不同…
阅读更多...
使用C++编写一个语音播报时钟（Qt）

使用C++编写一个语音播报时钟（Qt）

要求&#xff1a;当系统时间达到输入的时间时&#xff0c;语音播报对话框中的内容。定时可以取消。qt界面如上图所示。组件如下&#xff1a; countdownEdit作为书写目标时间的line_edit start_btn作为开始和停止的按钮 stop_btn作为取消的按钮 systimelab显示系统时间的lab tex…
阅读更多...
Java后端程序员简单操作Linux系统命令

Java后端程序员简单操作Linux系统命令

Linux系统概述 Linux 内核最初是由芬兰人林纳斯托瓦兹&#xff08;Linus Torvalds&#xff09;在赫尔辛基大学上 学时而编写的一个开源的操作系统。 Linux&#xff08;管理计算机硬件资源&#xff0c;任务调度&#xff09;支持多用户&#xff0c;支持网络&#xff0c;支持多线…
阅读更多...
Vue3：el-table实现日期的格式化

Vue3：el-table实现日期的格式化

后端如果返回的是时间戳&#xff0c;需要我们进行日期格式化 例如&#xff1a;2024-09-11T14:19:14 定义一个日期解析的工具组件 export function formatDateAsYYYYMMDDHHMMSS(dateStr: any) {const date new Date(dateStr);const year date.getFullYear();const month S…
阅读更多...
踩最深的坑，教会自己找到需求

踩最深的坑，教会自己找到需求

目录 引言 1. 寻找合适的需求 2. 海外市场选择 3. 线下热点判断 4. 线上关注度分析 5. 当前竞争分析 6. 未来潜力分析 引言 在经历了刻骨铭心的合伙创业经历后&#xff0c;我意识到是时候该独立出海了。 捡起早已深埋在心里的创业想法&#xff0c;开始独自创业。 这次…
阅读更多...
[笔记] 电机工作制以及软硬特性的本质推导

[笔记] 电机工作制以及软硬特性的本质推导

原始资料来源&#xff1a;某电机厂商 1.电机非常规操作术语和许可次数 1.1 电机操作术语 点动&#xff1a;通电后立即关停&#xff0c;最终速度不到额定转速的1/4电制动&#xff1a;制动到额定转速的1/3逆转&#xff1a;也就是打反车&#xff0c;不等停车&#xff0c;立即翻…
阅读更多...
stm32之硬件SPI读写W25Q64存储器应用案例

stm32之硬件SPI读写W25Q64存储器应用案例

系列文章目录 1. stm32之SPI通信协议 2. stm32之软件SPI读写W25Q64存储器应用案例 3. stm32之SPI通信外设 文章目录 系列文章目录前言一、电路接线图二、应用案例代码三、应用案例代码分析3.1 基本思路3.2 相关库函数介绍3.3 MySPI模块3.3.1 模块初始化3.3.2 SPI基本时序单元模…
阅读更多...
01_Python基本语法

01_Python基本语法

Hello Python 与其他编程一样&#xff0c;第一个程序都是输出Hello World!。 print("Hello World!")print() 函数由两部分构成 &#xff1a; 指令&#xff1a;print指令的执行对象&#xff0c;在 print 后面的括号里的内容 Hello World!。 Python程序的执行流程如…
阅读更多...
机器学习中最常见的50个问题（进阶篇）

机器学习中最常见的50个问题（进阶篇）

机器学习中最常见的50个问题 进阶篇 1.解释SVM的工作原理。 SVM&#xff0c;全称支持向量机&#xff08;Support Vector Machine&#xff09;&#xff0c;是一种有监督学习算法&#xff0c;主要用于解决数据挖掘或模式识别领域中的数据分类问题。 SVM的工作原理是建立一个最…
阅读更多...
【排序算法】之基数排序

【排序算法】之基数排序

一、算法介绍 基数排序是一种非比较型整数排序算法&#xff0c;其原理是将整数按低位到高位或者高位到低位的顺序&#xff0c;依次根据每一位的数值进行排序。通常情况下&#xff0c;基数排序会使用桶排序来处理每一位上的数值。 实现方法主要有如下&#xff1a; 最高位优先(…
阅读更多...
echarts实现湖南省地图并且定时轮询

echarts实现湖南省地图并且定时轮询

1、在HTML页面引入echarts.min.js <script src"https://cdn.jsdelivr.net/npm/echarts5/dist/echarts.min.js"></script> 2、实现代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"utf-8"><…
阅读更多...
如何搞定日语翻译？试试这四款工具

如何搞定日语翻译？试试这四款工具

写一篇字数800-1000字的软文&#xff0c;用翻译新手的角度分享福昕翻译在线、福昕翻译客户端、海鲸AI翻译以及彩云翻译在翻译日语时候的表现&#xff0c;要求口语化表达。 最近对于一些轻小说突然感兴趣了&#xff0c;所以我开始尝试各种翻译工具来帮助我搞定日语翻译。今天&am…
阅读更多...
仕考网：省考面试流程介绍，提前了解

仕考网：省考面试流程介绍，提前了解

省考面试流程介绍&#xff0c;一文带大家了解! 一、面试登记及抽签 考生通常需要提前10至30分钟到达指定地点进行登记。 考试工作人员核对考生身份证和面试通知书等相关证件后&#xff0c;进行抽签确定分组和进场顺序。 二、候考阶段 考生完成抽签后进入候考区等待考试。在…
阅读更多...
【LeetCode每日一题】2024年9月第二周（上）

【LeetCode每日一题】2024年9月第二周（上）

2024.9.9 中等 难度评分 1333 链接&#xff1a;2181. 合并零之间的节点 &#xff08;1&#xff09;题目描述&#xff1a; &#xff08;2&#xff09;示例 &#xff08;3&#xff09;分析 整体来说&#xff0c;描述还算清晰的题目&#xff0c;找到0节点所框定的区域&#xff0c…
阅读更多...
【iOS】UIViewController的生命周期

【iOS】UIViewController的生命周期

UIViewController的生命周期 文章目录 UIViewController的生命周期前言UIViewController的一个结构UIViewController的函数的执行顺序运行代码viewWillAppear && viewDidAppear多个视图控制器跳转时的生命周期pushpresent 小结 前言 之前对于有关于UIViewControlller的…
阅读更多...
cesium.js 入门到精通(3)

cesium.js 入门到精通(3)

天空盒子的设置 目前的地球背景 是 地图的cesium 我们想换成自己背景 // 设置天空盒skyBox: new Cesium.SkyBox({sources: {positiveX: "./texture/sky/px.jpg",negativeX: "./texture/sky/nx.jpg",positiveY: "./texture/sky/ny.jpg",negativ…
阅读更多...
如何构建高效快速的数据同步策略方案

如何构建高效快速的数据同步策略方案

在数据化的商业环境中&#xff0c;实现数据的实时同步不仅是提升企业内部协作效率的关键&#xff0c;更是确保业务决策精准性和时效性的核心要素。通过确保数据的一致性和最新性&#xff0c;企业能够实现跨部门的无缝协作&#xff0c;从而为业务流程的顺畅运作和快速响应市场变…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023