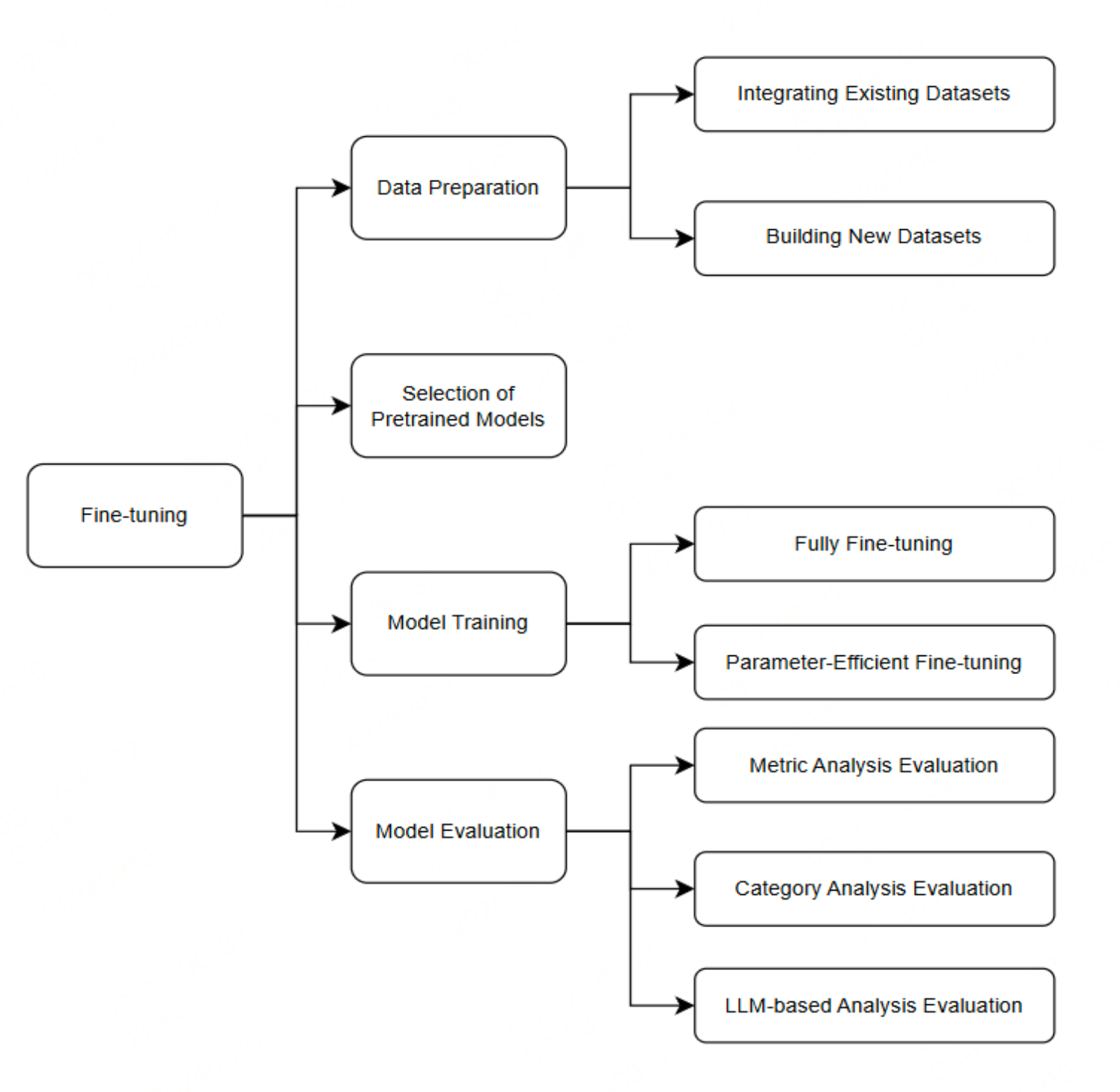
Comparison of spike sorting and thresholding of voltage waveforms for intracortical brain–machine interface performance
- 脑机接口性能的电压波形的尖峰分类和阈值比较
- 论文下载:
- 摘要
- 1 介绍
- 2 方法
- 2.1数据获取
- 2.2spike sorting 技术
- 2.3神经数据分析
- 3结果
- 3.1神经数据单元的质量与性能
- 3.2最好的RMs阈值系数用于解码
- 3.3解码的最佳固定电压阈值
- 3.4部分spikesorting
- 3.5基于小波包的spikesorting
- 4讨论
脑机接口性能的电压波形的尖峰分类和阈值比较
论文下载:
doi:10.1088/1741-2560/12/1/016009
摘要
目标。对于皮质内脑机接口(bmi),动作电位电压波形通常被分类以分离出单个神经元。如果这些神经元包含独立调节这一过程可以提高BMI的表现。然而,sorting行动电位(“尖峰”)需要高采样率,并且计算成本很高。显式地定义了尖峰sorting和其他方法的区别,我们量化了BMI解码器使用阈值交叉事件与分类动作电位时的性能。的方法。我们使用了两只恒河猴58个实验阶段的数据集犹他州的数组。数据被记录下来,同时动物们执行一项中心向外接触的任务七个不同的角度。对于sorting,神经信号通过使用一种混合的高斯函数来聚类波形的前四个主要成分。为阈值事件,仅超过设定阈值的峰值将被保留。我们解码了离线数据使用Naïve贝叶斯分类器达到方向和线性回归评估手的位置。主要的结果。我们发现阈值的最高性能是在将阈值设置在−3 ~−4.5 × vrm之间。峰值sorting数据优于阈值这是一种动物的数据,而不是另一种。平均Naïve贝叶斯分类精度为sorting数据为88.5%,数据阈值时平均变化5%。的意思是sorting数据的相关系数为0.92,平均变化0.015阈值。的意义。对于义肢的应用,这些结果意味着当使用阈值法代替尖峰排序,只有少量的性能损失。阈值事件的利用可能显著延长设备的使用寿命,因为这些事件通常在单个神经元不再孤立时仍然可以检测到。
1 介绍
脑机接口(BMIs)将脑电生理信号转换为辅助技术的命令信号,以帮助患有严重神经疾病的人。可以通过将多电极阵列插入大脑皮层1-2毫米来获取这些信息。这一领域的研究已经使非人类灵长类动物[3至8]和瘫痪患者[1至12]能够使用大脑信号来移动电脑光标。相关研究还表明,非人类灵长类动物[13]和人类[14至15]能够通过控制机械臂来为自己喂食。为了控制这些设备,需要使用来自运动皮层的动作电位,因为它们与运动学和动力学运动参数相关联。
突触分类是一种涉及检查每个记录电极的电压偏移并根据具有独特波形的动作电位(突触)进行区分的过程。它通常用于分析每个电极的电信号,以确定来自给定神经元的行动电位(18)。对于BMI应用,该过程在包含独立信息的神经元(19)的子集上最有用,这意味着它们各自更倾向于为特定目标或任务放电。然而,如果电极上主要只有一个神经元或包含具有相似调谐的神经元,相对于其他方法,突触分类预计不会提供显著的性能提升。此外,我们的先前研究发现,尽管单个神经元可能在数年内保持高于噪声水平,但随着时间的推移,它们彼此之间的可区分性会降低(20)。
突触分类还存在一些障碍,这使得神经假体从研究到临床的过渡更加困难(21)。它需要高采样率(~30000 s^-1),并且计算成本高昂,这可能会增加功率消耗。对可植入设备的电极进行分类。虽然一些研究小组已经在大量记录电极上实现了自动化过程(7, 19, 22, 23),但实时自动化算法很少应用,因为它们涉及到软件开发和硬件资源,这些资源可能并不容易获得。因此,目前尚不清楚是否值得花费时间和资源来进行电极分类。
目前有多种替代方法用于突触分类。可以通过使用多单元活动(MUA)来准确预测即将发生的动作,MUA是通过带通滤波数据、消除极端值并计算逐样本均方根(rms)电压来估算的 [24]。皮层局部场电位(LFPs)是兴奋性和抑制性树突电位的总和信号,也常用于预测动作 [25]。另一种方法是阈值化,已成为突触分类的日益流行的替代方法。该过程涉及为每个电极通道设置阈值,并检测每次电压潜力超过阈值的情况。该过程忽略了动作电位活动是否来自多个神经元 [8, 20, 21]。其优点是无需人工干预,既不费时也不费力。如果性能仍然足够高,对于长期植入系统来说可能是有益的,因为它可以降低每通道的功率需求。这可以用于减少电源限制或用于降低功耗的其他目的。可以为相同的电源添加额外的通道。
一些研究表明,复杂的运动可以通过不检测孤立的单个神经元来解码。一项最近的闭环研究使用了在植入数年后获得的阈值穿越事件,此时神经元的放电并不清晰[8, 20, 26]。他们使用了一种新的算法——ReFIT-Kalman滤波器,其性能比原始的velocity-KF算法提高了2.5倍,与真实手的中心-外-回移动控制效果相当[8]。Stark和Abeles通过使用阈值触发的放电和估计MUA,证明仅使用少量电极就可以准确地预测即将到来的运动[24]。Fraser及其同事的相关研究也表明,阈值处理与峰值检测相当[21]。在他们的研究中,来自一天在线实验测试的四个数据集表明,阈值数据有时可以优于峰值检测数据。另一方面,Todorova等人最近的研究得出结论,基本的峰值检测方法优于低阈值波形穿越方法[27]。由于这些相互矛盾的研究,因此需要更多的研究来确定哪种方法最适合用于解码复杂的运动。采用不同的阈值放置技术,对于排序数据与未排序数据的性能表现,目前尚无法得出一般性的结论。为了更好地理解这些相互矛盾的结果,有必要在大量数据集上评估各种阈值以及不同神经元子群的贡献。
在这项研究中,我们量化了两种动物在脉冲分类和阈值之间的性能差异使用58个每日数据集。其他研究分析了不同尖峰sorting方法的性能[28],MUA[24,28]和lfp[24,28 - 36]。据我们所知,这是第一个使用综合数据集的研究最佳阈值水平除了量化不同之间的解码器性能的尖峰排序和阈值。这也是为数不多的比较单神经元解码器性能,单神经元具有噪音污染最小,多神经元,还有
这些单元类型的组合。我们使用Naïve贝叶斯分类和线性回归分析性能单个神经元和多个神经元,均方根电压阈值,固定电压阈值,和尖峰sorting只有一个信道的子集。当部分尖峰排序时,我们也评估给予最高评价的渠道的特性当sorting时,表现最差。
2 方法
到目前为止,
2.1数据获取
斯坦福大学动物护理和使用委员会批准了所有协议。本研究中使用的数据和训练方法与[20]中使用的方法相同。两只恒河猴,L和I,对28个潜在的视觉目标执行了一个中心外到达任务,有4个距离和7个角度。在我们的分析中,这些都被分解成7个分类的角度。这项任务是在完全黑暗的情况下在正面平行屏幕上执行的(图1(a))。在食指或中指的远端关节上放置反射珠子,光学跟踪手的运动。使用北极星系统(NDI,滑铁卢,安大略省,加拿大),以60个样本s−1(标称亚毫米分辨率)的速度获得手部运动。该任务使用Tempo软件(反射计算,圣路易斯,密苏里州)进行排序。在本研究之前,这些动物被训练了好几个月;因此,很可能很少或没有学习。实验通常持续1-5小时,实验成功的动物会获得果汁奖励。
通过标准的神经外科技术将每个动物植入PMd/M1阵列。数据使用硅“犹他”阵列(贝莱德技术,盐湖城,UT,美国)记录,由100个微电极组成,在10×10网格上,中心间距为400 μm。当数据收集开始时,Monkey L和I的阵列分别是11个月和7个月大,有大量的单单位活动。使用Cerebus系统(贝莱德微系统,盐湖城,UT)在猴子L和I中记录6周和8周(图1(b))。在这些时间段内获得了69个每日数据集,但只分析了58个,因为我们只使用了每个目标超过100个达到范围的数据集。
采用贝莱德的内置函数计算均方根电压,与标准计算略有不同。他们的算法计算了尖峰数据流噪声的均方根电压的有偏估计。在下面的方程中,si表示过滤后的30 kHz采样峰值流,xi表示均方值。式(1)计算了一组600个连续样本的一个Vrms值。它只做了两秒钟,结果是得到100个均方值。在公式(2)中,这些值中最低的5个被丢弃,接下来的20个被用于计算最终的均方根电压。这种方法的基本原理是避免由于存在大伪而膨胀Vrms值。

2.2spike sorting 技术
我们使用[19,20,37]中描述的尖峰分选方法来可视化和识别与不同神经元相关的动作电位。所有神经数据均在MATLAB(MathWorks,Natick,MA,USA)中进行离线分析。虽然闭环研究目前是黄金标准,但我们进行了开环分析,因为我们想使用不同的技术来分析相同的数据。简单地说,对数据进行了高通滤波,以消除局部场的波动。当信号超过一个相对于其均方根电压的阈值时,在超过阈值前后分别记录一个短的电压段。非常大的“榨汁机”制品也被消除在触发峰值后1毫秒的“单位”。这些罕见的试验间事件不会影响解码器的性能,但对于另一项使用该数据的识别最大单个单元[20]的研究存在问题。接下来,剩余的数据随时间移动,以对齐所有的峰值。然后对数据进行噪声白化,得到波形片段的前四个主成分。采用“松弛器”拟合了混合高斯模型。
每个通道的波形根据其形状、振幅和主成分进行分类。图1。(a)一只猴子在完全黑暗的环境中,在额平行屏幕上执行中心向外伸展的任务。(b)植入的时间轴和记录从犹他州阵列。©在尖峰分类过程中波形如何分类的可视化解释。3 J.神经工程12(2015)016009BPCristt等人(图1©)。

我们将波形分为假定的单个神经元(类别“4”)、受其他单元污染最小的单个单元(类别“3”)和多单元(类别“2”或“1”)。第一类单元可能受到噪音污染,但仍然出现模糊的神经。第2类波形具有更明显的神经特征,但它们由一个质心描述,在主成分分析(PCA)中,中心“散列”没有明确描述。在分析主成分时,第3类波形有一个清晰勾画的质心,在外环上有一些重叠的单元。在创建阈值化的数据集时,没有发生这种单元分类。对于阈值数据集,对所有超过设定阈值水平的波形进行分析,而不管其表观质量如何。在两种分析中都使用了相同的电极。
为了演示如果使用其他复杂的技术对动作电位进行排序,解码器的性能将如何变化,我们还执行了Quiroga等人[38]描述的无监督小波峰值排序算法。每个峰值采用4级Haar小波变换进行分解。然后,根据修正的柯尔莫戈罗夫-斯米尔诺夫检验,从每个信道中选择10个偏离正态性最大的小波系数。然后使用Potts模型超顺磁聚类(SPC)方法对其进行聚类。我们使用Quiroga等人提供的软件进行此分析(www.vis.caltech.edu/∼rodri/Wave_clus/Wave_clus_home.htm)。
为了检测神经单元,我们首先使用自动小波分类算法对96个通道中的每个通道进行峰值排序。然后,我们手动调整了SPC的参数,以进一步改进基于聚类波形相似性的视觉检查的我们的排序结果。SPC被限制为每个通道产生不超过8个集群,但可识别的集群的典型数量为2-4个。我们将该算法应用于猴子I记录的第一天和猴子L记录的前两天。
2.3神经数据分析
本研究还应用了[20]中使用的两种离线神经解码器。我们使用朴素贝叶斯分类作为离散神经解码器来计算我们预测目标选择[7]的准确性。我们将目标呈现后的500 ms时间窗内每个通道的发射率建模为泊松分布。采用公式(4)和(5)计算每个目标的可能性,其中Θ为实际目标角度,θ为预测角度,yn为神经元N上出现的峰值数量,Y表示观察到的峰值向量,N为神经元数量。

我们选择了使这种可能性最大化的目标。我们在同一天内使用10倍交叉验证来训练和测试了这个模型。我们使用一个正确百分比变量来评估性能,该变量表明我们能够正确预测选择哪个目标的频率。
此外,我们使用一个连续离线线性解码器来预测动物的手位置[39]。对于每个试验,数据被分成100个ms的箱子,我们找到了每个箱子的平均发射率和手的位置。我们还使用了10个连续100 ms时间滞后的发射率信息。使用线性维纳滤波器,我们将手的位置建模为每个通道的发射率的函数。在等式(6)中,矩阵X包含了每个箱子的平均水平和垂直位置。矩阵Y的每一行都包含了每个神经元在10个连续的时间滞后时的放电率。矩阵B是通过线性回归计算出来的,是由此得到的线性解码器。

我们在同一天内使用20倍交叉验证来训练和测试了这个模型。利用预测和实际手位置之间的相关系数给出了连续性能。为了验证线性回归解码器的准确性,我们还测量了解码到达过程中“到目标的平均距离”,并在阈值分析中比较了这两个指标。到目标的平均距离度量表示在到达[40]期间的所有时间步长中到外围目标的平均距离。具有均匀速度的最佳到达目标的平均距离等于总距离的一半。
3结果

3.1神经数据单元的质量与性能
为了确保我们正在分析的数据能够代表常见的数据集,我们评估了几个特征。图2显示了这两种动物在第1天的峰值面板,表1给出了单位类型的分布。这两种动物都表现出相似的趋势,即大多数波形包含多个单位的混合物,而最少的则代表单个单位。对于Monkey L,40%的排序波形是有噪声的第1类波形,只有19%是单个单元。47%的猴子I的波形是第1类,只有12%是单个单位。这些单元分布是典型的“好”阵列。图3(a)显示了所有数据集之间的均方根电压。猴子L的平均均方根电压为14.53 μV,猴子I的平均均方根电压为9.22 μV。

图3(b)显示了这两种解码器在使用不同的峰值排序数据子集时的性能。当分析尖峰排序数据时,没有去除具有低发射率的通道。因为可能有大型的低发射单位,当它们被包括在内时,性能更高。它们的存在确保了我们在与阈值进行比较时没有特别不利于尖峰排序。第2类波形可能对应于多个神经元,与其他单独类别相比,在分离和分析时的表现最高。此外,当使用类别2和类别3时,当将单个单元加入分析时,性能值仅得到最小的改善,尽管改善具有统计学意义(t检验,p < 0.01)。当分析评分为2到4的单位时,它们表现出最好的整体性能,标准差最小。猴子L的朴素贝叶斯正确率分别为94%和83%,相关系数分别为0.94 (L)和0.90 (I)。这个尖峰排序数据的子集是我们用作其余分析的比较。
3.2最好的RMs阈值系数用于解码
研究人员通常使用正方根电压来设置一个阈值[8,21,41,42]。为了定量地确定最佳位置,我们测试了从−3×Vrms到−18×Vrms的不同阈值水平的解码器性能(图4(a))。去除发射率<为1Hz的通道。对于朴素贝叶斯解码器,猴子L的最佳阈值水平为−4.5×Vrms,猴子I的水平为−3×Vrms。

这些阈值产生的朴素贝叶斯百分比正确值分别为90% (L)和89% (I),概率≈为14%。猴子L的−4×Vrms的相关系数最好,ρ=为0.92。对于猴子I,它在−3×Vrms上被看到,并产生了ρ = 0.89。
我们使用到目标指标的平均距离来证实相关系数的趋势,我们发现这两个指标显示出相似的性能趋势。猴子L的最佳阈值水平更高,可能是因为数组更老,可能包含更多的噪声。对于Monkey I,spike排序的数据的性能略低于阈值交叉事件。此外,猴子I的阈值分析没有包含一个峰值。−3×Vrms的阈值,平均约为−28μV,最初是在记录期间设置的,对于这个较新的阵列来说可能还不够低。对于Monkey L,最优阈值数据的解码器性能仅略低于尖峰排序数据,尽管差异具有统计学意义(p < 0.001)。对于Monkey I,阈值数据的朴素贝叶斯性能在统计学上显著高于峰值排序数据(p = 2.4×10−11),但线性回归性能没有显著差异(p = 0.908)。
3.3解码的最佳固定电压阈值
一些芯片设计对每个通道使用一个固定的电压阈值,而不是使用通道的均方根电压。如果均方根电压的平均值和标准差相当紧,这种方法可以很好地工作。为了测试我们的数据集将如何使用这种技术,并确定哪个固定电压阈值将最大化性能,我们测试了−10μV和−200μV之间的阈值解码器。去除发射率<为1Hz的通道。性能如图4的最下面一行所示。对于朴素贝叶斯解码器,猴子L在−70μV时的性能最好,产生的PC =为88%。猴子I在−10μV,可能的最低值,给PC = 89%。在−50μV时,猴子L和L的相关系数最好−10μV。这生成了ρ = 0.92 (L)和ρ = 0.90 (I)。线性回归分析中的最优阈值与到目标分析的平均距离中所看到的阈值相匹配。对于这两种动物,由于在记录期间最初设置的阈值水平,与−10到−30μV的阈值水平相关的表现几乎相同。对于Monkey L,最优阈值数据的性能仅略低于峰值排序数据,尽管差异具有统计学意义(p < 0.001)。对于Monkey I,阈值数据的朴素贝叶斯性能在统计学上显著高于排序数据(p = 2.7E−11),尽管线性回归性能没有显著差异(p = 0.912)。
3.4部分spikesorting
如果在使用阈值而不是峰值排序时解码器性能受损,则可能对数据子集进行峰值排序以重新获得该性能。为了确定哪些通道最适合进行尖峰排序,我们在第1天测试了每个通道的单个解码器性能。对于每个电极,当阈值数据被删除并替换为相应的尖峰排序数据时,测量性能。然后,我们对第1天[43]改善最高的通道进行排名,并在第2天及以后对它们进行测试。我们在剩余数据集上对最佳通道、第二优通道等进行尖峰排序后的性能。对于部分尖峰分类分析,没有去除低发射率的通道。低发射率的通道每天都不同,这将干扰我们对相同电极进行排序和测试的能力。这种分析主要被用作一种工具,以识别在这两种动物中受穗突分类或阈值影响最大的通道。

图5(a)表明,随着更多的电极被尖峰排序,猴子l的解码器性能有所提高。这些趋势是基于我们之前的发现,即排序数据优于该动物的阈值数据。来自Monkey I的结果没有显示出来,因为阈值化后的数据优于排序后的数据,而该分析主要集中在恢复阈值化过程中的性能损失。如果有26个猴子L的通道被尖峰排序,则线性回归性能与完全尖峰排序的数据不再有统计学差异(p = 0.06)。在仅对6个通道进行峰值排序后,相关系数在完全峰值排序时的1%以内。另一方面,必须对76个通道进行排序,直到获得的朴素贝叶斯性能没有显著差异(p = 0.051)。斯派克排序的61个频道带来了天真贝叶斯精度在1%以内的表现时,完全峰值排序的猴子L在执行部分尖峰排序分析时,当通道被排序数据替换时,解码器性能的改善最高。
除上述分析外,我们还分析了两种动物的四个最佳和最差通道的特性。正如预期的那样,进行尖峰排序的最佳通道包括多个具有独立调优属性的单元。另一方面,最差的尖峰排序通道表明,我们的尖峰排序技术的手动方面偶尔也有缺陷。例如,在峰值排序过程中,没有明显双极形状的波形被移除,但它们偶尔包含有用的信息。此外,几乎不可能在视觉上区分有用的散列和噪声。两个单元将看起来非常相似,但只有其中一个导致解码器性能的改善时,峰值排序。Wood及其同事的研究支持了这一说法,发现对于人工排序合成数据[28],平均错误率为23%,假阳性和假阴性为30%。最后,我们发现,我们的尖峰分类器的自动部分偶尔会把一个好的单元分解成多个尖峰,这可能使信号噪声更大和不那么有用。
3.5基于小波包的spikesorting
为了公平地表示其他尖峰排序算法的性能,我们执行了一个无监督的,小波尖峰排序算法[38]。与主成分分析不同,小波系数由于小波分解的时间尺度特性,能更好地识别动作电位的时间特征。此外,SPC提供了一种更一般的聚类方法,既不需要在特征空间中不重叠的聚类,也不需要假设特定的分布(如我们原始的高斯期望最大化聚类方法)[38]。我们在三个数据集上测试了小波排序算法,以确保一个良好的近似。如图5(b)所示,小波分类数据和我们的pca聚类数据在解码器性能上的差异非常小。因此,我们得出结论,在我们的分析中,执行基于pca的峰值排序方法是可以接受的。
4讨论
我们已经证明,阈值跨越事件可以用于分析BMI数据,而不是尖峰排序,而不会导致性能的大幅下降。朴素贝叶斯百分比正确率平均变化5%,相关系数变化0.015。基于我们的神经数据的质量和性能,它似乎代表了常见的bmi。我们的结果表明,−3和−5×Vrms之间的阈值会导致相似的性能。虽然本研究包含有限数量的阵列,但我们假设,对于噪声较小的阵列,最佳均方根阈值在−3×Vrms左右。对于噪声较大的阵列,最佳阈值可能约为−4.5×Vrms。它是不可能确定一个固定的电压阈值,将工作在每个数据集,因为特征是不同的患者。固定阈值通常会提供较低的性能,并且还需要用户手动调整阈值。MonkeyL数据的解码器性能表明,峰值排序数据的性能略高于阈值数据,尽管朴素贝叶斯精度仅高于4%,相关系数仅高于0.02。虽然这仍然需要人工干预,但我们的部分尖峰排序分析表明,任何由于阈值化而导致的性能损失,在对一小部分通道进行尖峰排序后,都可以恢复。要排序的最佳和最差通道的波形特征没有显示出任何一致的趋势,所以在选择要进行尖峰排序的通道子集时,我们不可能准确地说要寻找哪些特征。虽然当有多个具有独立调优特性的单元时,尖峰排序是有利的,但调优特性不能仅通过检查来确定。此外,几乎不可能在视觉上区分有用的散列和噪声。文图拉[44]的算法在部分尖峰排序分析中很有用,因为它决定了单元是应该未排序还是根据导致最高解码器性能的内容进行排序。
另一方面,猴子I中的峰值排序和阈值数据显示了不同的结果。相关系数无显著性差异。此外,对于朴素贝叶斯分类,阈值数据的性能实际上高于排序数据。这可能是由于不必要的单元分裂由自动部分的穗分类器在弗雷泽和他的同事进行的一项研究中,两种动物之间的相反结果,在一种情况下,spike排序数据优于未排序数据,而另一种[21]则不是。我们的结果与Gilja等人、Stark和Abeles的研究结果一致,因为我们证明了复杂的运动可以在不检测到峰值[8,24]的情况下被解码。然而,Todorova等人最近发表的研究得出结论,尖峰排序增加了在BMI解码[27]中使用的阈值交叉方法的价值。在他们的研究中,阈值水平设置为了最大化的能力执行峰值排序猴子图2显示,许多这个动物的阈值振幅高于最优水平我们看到,这往往会阻碍解码器性能阈值数据(见我们的图4)。他们证明,与OLE未排序数据相比,最优线性估计器(OLE)振幅排序数据导致了∼12%的性能增益。在我们的研究中,对于猴子L,阈值为−6.5×的Vrms也会导致排序后的数据比阈值数据高出12%。在他们的研究中,来自其他动物的数据的阈值比带通滤波电压轨迹的平均值低三个标准差,这导致了阈值水平更类似于我们的阈值水平。随后,OLE振幅排序数据的∼仅比OLE未排序数据好6%,这与MonkeyL的结果更一致从我们的研究。
我们的研究得出结论,如果你系统地扫描阈值,就有可能找到一个范围,其中阈值跨越基本上和峰值排序一样好。使用阈值交叉而不是尖峰排序将使它更容易构建植入式修复处理器和芯片与阈值交叉探测器[45]。需要注意的是,我们的分析是离线执行的,而且我们的排序方法并不是完全自动化的。其他的研究,如托多洛瓦等人的研究,在更多的解码器中也发现了类似的结果。如果存在大量的噪声或运动伪影,我们的结论并不成立,尽管这些噪声很少在保持单元完整的同时阻碍阈值跨越。事实上,在通常有很短的电线和良好的屏蔽[45]的无线系统中,噪声伪影往往较低。据我们所知,这是第一个除了在分析大量数据集中不同神经元亚群的贡献外,还确定最佳阈值水平的研究。利用目前的微电极阵列技术,我们的研究表明,阈值化和尖峰分选基本上可以互换使用,而不会看到性能的显著下降。由于硬件和软件更简单,阈值跨越事件的利用可以使BMI设备更容易地从研究过渡到临床。这也允许具有较低功耗的长期系统,它可以应用于具有大量电极通道的系统。