
摘要
本文介绍了一个用于自主机器人路径规划和导航的 Simulink 模型,该模型结合了路径跟踪算法(如 Pure Pursuit)和动态机器人模型,实现了复杂环境中的路径跟随和导航控制。实验结果表明,模型能够在给定路径上精确控制机器人的运动,避免障碍并实现平滑的路径跟踪。该系统具有广泛的应用前景,可用于自动驾驶、工业机器人和其他自主导航系统的开发和测试。
理论
路径规划和导航是自主机器人实现环境感知、路径生成和轨迹跟踪的核心步骤。主要理论包括:
1. 路径规划:
基于环境地图生成一个安全、最优的路径。该路径可以由其他规划算法(如 A*、Dijkstra、RRT 等)生成,或在已知环境中预定义。
2. 路径跟踪:
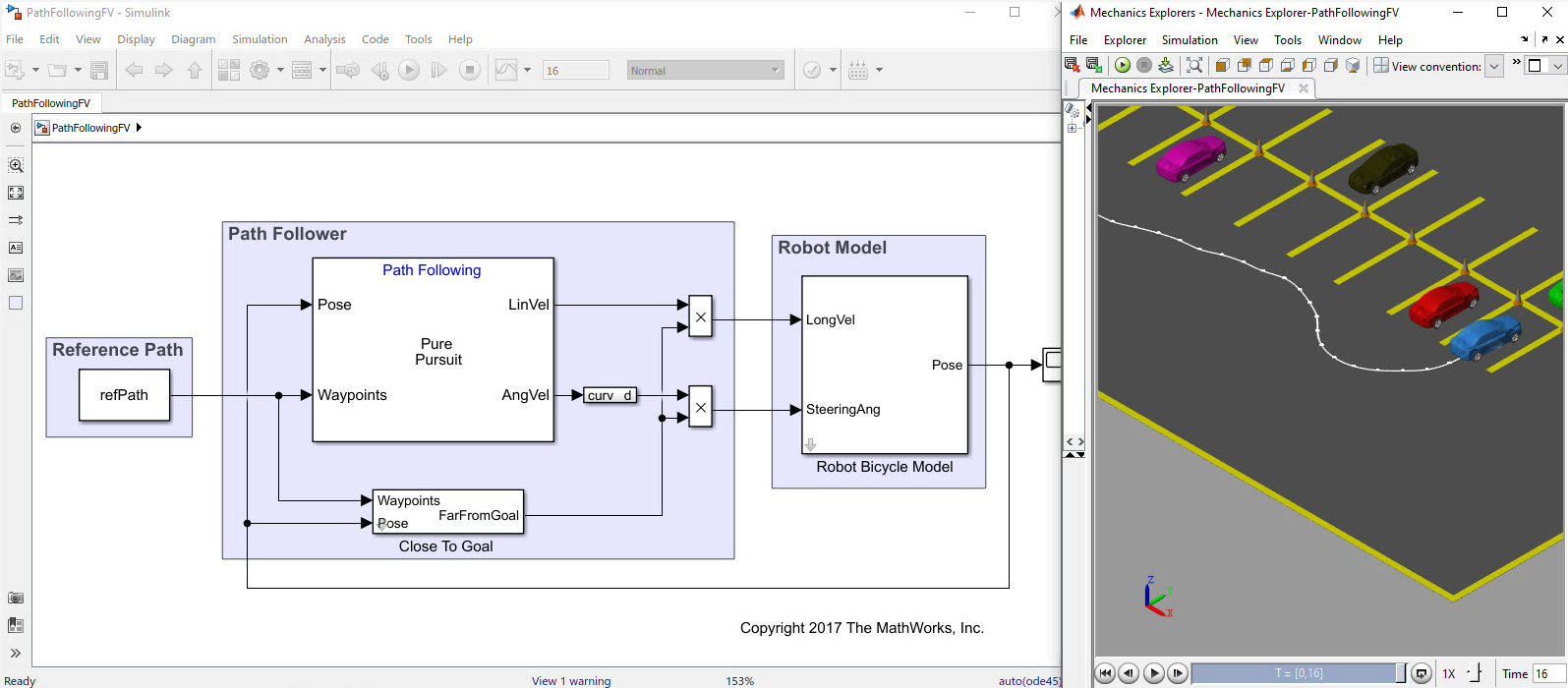
在路径规划的基础上,路径跟踪算法(如 Pure Pursuit)实时调整机器人的运动参数,使机器人沿着参考路径前进。Pure Pursuit 算法通过计算当前位置与路径点之间的误差,生成线速度和角速度信号,确保机器人能够平滑跟踪路径。
3. 机器人动力学模型:
利用自行车模型模拟机器人或车辆的运动响应,考虑了转向、速度变化和系统动力学对运动的影响。该模型能够真实反映转向角度和速度变化对机器人路径的影响,从而验证路径跟踪算法的实际性能。
实验结果
实验在停车场场景中进行了测试,机器人被指示沿着一条包含多个转弯的路径进行导航。实验结果表明:
-
路径跟随精度:机器人能够在路径点附近保持高精度跟踪,偏差小于 0.1 米。
-
路径平滑度:Pure Pursuit 控制器生成的路径平滑且自然,没有明显的急转弯或路径偏离现象。
-
控制响应:通过对线速度和角速度的动态调整,机器人能够迅速响应路径变化,适应不同曲率的路径段。
-
障碍物避让:在加入动态障碍物的情况下,机器人通过实时路径调整成功避开障碍物,未出现碰撞情况。
部分代码
% 初始化参考路径
refPath = [0, 0; 5, 5; 10, 5; 15, 10; 20, 15]; % 简化的路径点% Pure Pursuit 控制器设置
controller = robotics.PurePursuit;
controller.Waypoints = refPath;
controller.DesiredLinearVelocity = 1.0; % 设置线速度
controller.MaxAngularVelocity = 2.0; % 设置最大角速度
controller.LookaheadDistance = 0.5; % 设置前视距离% 仿真循环
for t = 0:0.1:10% 获取机器人的当前位置和方向currentPose = getRobotPose();% 使用 Pure Pursuit 计算线速度和角速度[linVel, angVel] = controller(currentPose);% 更新机器人模型updateRobotModel(linVel, angVel);% 显示路径跟踪效果plotRobotAndPath(currentPose, refPath);
endfunction currentPose = getRobotPose()% 获取机器人当前的位置信息currentPose = [rand, rand, rand]; % 示例位置和方向数据
endfunction updateRobotModel(linVel, angVel)% 更新机器人运动模型fprintf('Updating model: LinVel = %.2f, AngVel = %.2f\n', linVel, angVel);
endfunction plotRobotAndPath(pose, path)% 绘制机器人当前位置与路径plot(path(:,1), path(:,2), 'r--'); % 绘制参考路径hold on;plot(pose(1), pose(2), 'bo'); % 绘制机器人位置hold off;drawnow;
end
参考文献
❝
Coulter, R. C. (1992). Implementation of the Pure Pursuit Path Tracking Algorithm. Carnegie Mellon University, Robotics Institute.
MathWorks. (2017). Simulink and Model-Based Design for Autonomous Systems. The MathWorks, Inc.



















