给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:

输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
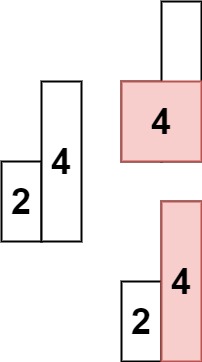
输入: heights = [2,4] 输出: 4
提示:
1 <= heights.length <=1050 <= heights[i] <= 104
思路都在代码注释里,自己看,看不懂的留言或者私信,看到第一时间解答
class Solution {/**这个题第一感觉是用的单调栈的解法,这个最大的矩形必定以某一个柱子的高度为最低高度我们对于每个柱子,求出它左边第一个比它小的(left)和右边第一个比它小的(right)则right-left-1就是以这个柱子为最低高度的矩形的宽度所有的这些宽度*高度里的最大值就是我们的答案*/public int largestRectangleArea(int[] heights) {/**如果只有一个,那没啥说的,返回它的高度就行了,因为它的宽度是1 */if(heights.length == 1) {return heights[0];}/**如果是两个,我们可以特殊处理也可以不特殊处理,这里我不特殊处理了,直接用单调栈来处理单调栈的核心是nearLess数组,我们使用单独的方法去求这个*/int[][] nearLess = getNearLess(heights);/**有了这个数组之后我们就可以直接比较求答案了 */int ans = 0;for(int i = 0; i < heights.length; i++) {/**我们这里left和right可以直接用,因为我们在getNearLess里已经取巧处理了 */int left = nearLess[i][0];int right = nearLess[i][1];ans = Math.max(ans, (right - left - 1) * heights[i]);}return ans;}public int[][] getNearLess2(int[] heights) {/**定义返回结果 */int[][] nearLess = new int[heights.length][2];/**定义单调栈,我们栈里的数据是栈底到栈顶依次变大的,也就是栈顶是最小值,如果出现更小的就把大的弹出 */Stack<Integer> minStack = new Stack<>();/**遍历数组依次入栈 */for(int i = 0; i < heights.length; i++) {while(!minStack.isEmpty() && heights[minStack.peek()] > heights[i]) {/**把大的弹出 */int popIndex = minStack.pop();/**i是造成popIndex这个数弹出的,也就是右边第一个小于它的数的下标 */nearLess[popIndex][1] = i;/**popIndex左边第一个比它小的是它压着的,如果下面没了(栈空了),就写-1*/nearLess[popIndex][0] = minStack.isEmpty()? -1 : minStack.peek();}/**当前已经满足放入的条件了,放入当前数 */minStack.push(i);}/**结算栈中剩余的元素 */while(!minStack.isEmpty()) {int popIndex = minStack.pop();/**剩余需要结算的数右边没有比它小的,这里就写heigths.length了,这里是为了主方法计算方便,一般别的地方我写-1 */nearLess[popIndex][1] = heights.length;/**popIndex左边第一个比它小的是它压着的,如果下面没了(栈空了),就写-1*/nearLess[popIndex][0] = minStack.isEmpty()? -1 : minStack.peek();}return nearLess;}public int[][] getNearLess(int[] heights) {/**定义返回结果 */int[][] nearLess = new int[heights.length][2];/**定义单调栈,我们栈里的数据是栈底到栈顶依次变大的,也就是栈顶是最小值,如果出现更小的就把大的弹出,这里我替换成数组用于节约常数时间 */int[] minStack = new int[heights.length];int stackSize = 0;/**遍历数组依次入栈 */for(int i = 0; i < heights.length; i++) {while(stackSize != 0 && heights[minStack[stackSize - 1]] > heights[i]) {/**把大的弹出 */int popIndex = minStack[--stackSize];/**i是造成popIndex这个数弹出的,也就是右边第一个小于它的数的下标 */nearLess[popIndex][1] = i;/**popIndex左边第一个比它小的是它压着的,如果下面没了(栈空了),就写-1*/nearLess[popIndex][0] = stackSize == 0? -1 : minStack[stackSize - 1];}/**当前已经满足放入的条件了,放入当前数 */minStack[stackSize++] = i;}/**结算栈中剩余的元素 */while(stackSize != 0) {int popIndex = minStack[--stackSize];/**剩余需要结算的数右边没有比它小的,这里就写heigths.length了,这里是为了主方法计算方便,一般别的地方我写-1 */nearLess[popIndex][1] = heights.length;/**popIndex左边第一个比它小的是它压着的,如果下面没了(栈空了),就写-1*/nearLess[popIndex][0] = stackSize == 0? -1 : minStack[stackSize - 1];}return nearLess;}
} 



















