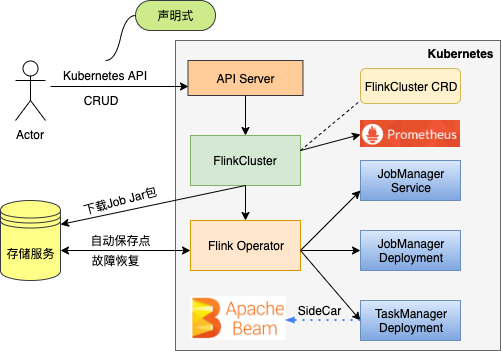
Link：https://wiselabcmu.github.io/dart/
Publish： 2024CVPR

Abstract

DART主要任务就是用来合成雷达距离多普勒图像range-droppler，可用于生成高质量的断层扫描图像。

Related Work

1 Radar Simulation

• 基于模型的方法

任务：使用物理和环境模型模拟雷达信号的传播
方法：使用光线追踪、有限元建模（FEM）或有限差分时域（FDTD）模拟的某种组合
缺点：不能够从雷达数据中推断环境的结构；准确性受到用户创建雷达真实环境模型的能力的限制。

• 数据驱动的方法

方法：使用真实传感器扫描建立环境模型，主要分为稀疏方法和密集方法（相干聚合和非相干聚合）

2 雷达中的机器学习方法

3 NeRF

三个组件：

• 世界模型：世界定义为每个位置和视角的RGB和透明度
• 世界表示
• 渲染函数和模型反演

DART

主要工作：

• 选择距离多普勒的度量表示去克服紧凑雷达分辨率差的问题
• 使用网络模型考虑了电磁波相互作用的效应
• 使用自适应网格世界表示的网络架构，设计距离多普勒方法，优化了渲染过程

1 距离多普勒表示

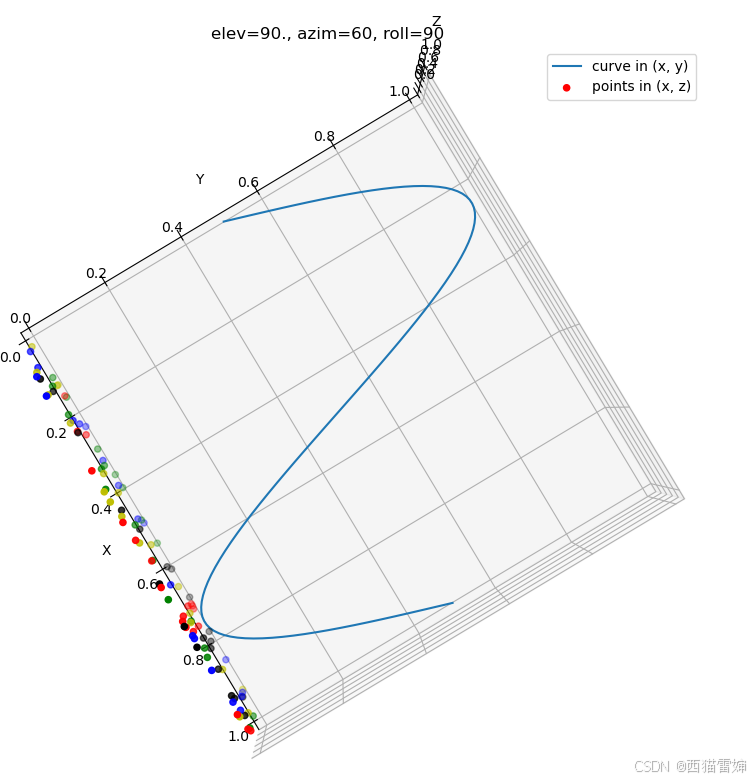
不同的点的多普勒速度是不一样的，在3D空间中，每个相同的多普勒值（红色的球体）对应一个圆锥体（圆锥体），球体和圆锥体的交集构成多普勒像素。

左图相当于圆锥体的侧视图，右图为立体图。

2 雷达预处理

3 DART的世界模型

以数据驱动形式对属性进行建模，使用基于视图的神经网络方法来表示反射率和透射率。

建模射频反射

空间中点的属性：反射率（反射回来的能量比例）和透射率（穿过去的能量比例）

将目标特性分为反射系数和透射系数。

世界表征

用自适应的grid的Instant NGP（Instant Neural Graphics Primitive）作为backbone。

网络输出：基础反射率 $\overline{\sigma }$ 和渗透率 $\overline{\alpha }$、共享球谐系数（其作为内积应用于入射角）

激活函数：$\sigma$ 是无界的，应用线性激活函数； $\alpha$ 应用 $f(\alpha )=exp(max(0,\alpha ))$ 激活函数；

4 雷达渲染和模型训练

使用可微映射来训练 $\sigma$ 和 $\alpha$，该映射从给定的 $(\sigma ,\alpha )$ 网络生成多天线距离多普勒热图，将此称为雷达渲染。

光线追踪

雷达从位置 $x$ 处发出一条射线，射线的方向由旋转矩阵 $\mathbf{A}$ 确定，射线以 $\omega$ 角度发射，这个角度决定光线遇到物体表面时的碰撞方向。

当光线在空间中传播时，它会经过路径上的不同点。每个点可以用 $x+r_i\omega$ 表示，$r_i$ 表示从雷达到该点的距离。这些点上，光线信号有一个振幅 $u_i$ ，随着距离增加，由于自由空间路径损耗振幅会减小。

信号到达某一点时，以振幅 $u_i\sigma (t_i)$ 反射，以 $u_i\alpha (t_i)$ 继续向前传播。当反射信号返回到雷达时，它会再次受到与距离 $r_i$ 成正比的衰减，意味着信号传输距离越远，衰减越严重。

距离 $r_1,r_2,\cdots ,r_N$ 表示离散的距离区间，雷达在这些区间上采样回波信号。振幅C表示在特定位置处接受到的信号强度：

多普勒积分

在特定位置和速度下，将雷达信号的返回值整合到一个多天线的范围-多普勒热图中。

多普勒速度采用 $⟨\omega ,v⟩$ 计算，和雷达入射方向和速度有关，说明多普勒频移是由目标的相对运动引起的。
可以沿着每个范围-多普勒单元对应的薄环对返回信号 $C$ 进行积分：

之后需要对离散单元的宽度进行修正，以考虑不同距离和速度下的变化。具体用M个随机方向 ${\omega }_1,\cdots ,{\omega }_M$ 来近似积分，这些方向满足条件 $⟨\omega ,v⟩=d_j$ ：

通过这些步骤可以得到一个经过调整和修正的雷达信号热图，用于分析雷达回波信号在不同距离和速度上的分布情况。

优化渲染

主要是提高渲染速度和效率。

传统做法：将每个（距离、多普勒、天线）“像素”都视为一个独立的采样点进行处理，那么计算成本会非常高。这种方法类似于在神经辐射场（NeRF）中的标准实践。这种方法需要对场函数进行大量次的采样，包括在距离、多普勒、天线、距离积分和多普勒积分上的多次采样，以渲染出一张图像。

优化：在渲染时同时处理具有相同多普勒值的所有区间（bins），从而重复使用 $\sigma$ 和 $\alpha$ 的采样。可以显著减少场函数的评估次数，因为多个像素可以共享相同的采样结果，从而避免了重复计算。