重叠区间专场。

452.用最少数量的箭引爆气球

题目:452. 用最少数量的箭引爆气球 - 力扣（LeetCode）

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足  xstart ≤ x ≤ xend(挨在一起可以射爆），则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

 

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

气球的坐标由二维数组 points 给出，每个气球的范围由 points[i][0]（左边界）和 points[i][1]（右边界）表示 

局部最优，只要两气球间有重叠区间，就可以射爆以达到全局最优把所有气球射爆用的最少的箭术。 

首先按照起始位置排序气球，遍历数组时比较当前气球的初始值是否大于上一个气球的末尾值。而下下一个如果需要同时射爆，就也要初始值比前前一个气球的末尾值小，否则就跳过上一个数组，箭+1。看看下一个气球是否有重叠区间。

代码 

class Solution {
public:static bool cmp(const vector<int>&a,const vector<int>&b){return a[0]<b[0];//按照初始位置升序排列}int findMinArrowShots(vector<vector<int>>& points) {sort(points.begin(),points.end(),cmp);if(points.size()==0)return 0;int result=1;//因为不为空，所以至少需要一支箭for(int i=1;i<points.size();i++)//从第二个气球开始{if(points[i][0]>points[i-1][1])//如果当前气球的初始值大于当上一个气球的末尾值，证明两气球不重叠{result++;}else//如果有重叠的话，那么更新当前气球的末尾值为和上一格气球的末尾值比较的最小值，下一个气球的初始值只有大于该值，才能一起射爆，否则就要多一支箭{points[i][1]=min(points[i-1][1],points[i][1]);}}return result;}
};

 满足 xstart ≤ x ≤ xend，则该气球会被引爆。那么说明两个气球挨在一起不重叠也可以一起射爆，

435.无重叠区间

题目：435. 无重叠区间 - 力扣（LeetCode）

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

注意 只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。

示例 1:

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

两中写法，左边界排序和右边界排序。这里因为我刚做上一题（两道题还是挺像的），所以就先使用左边界排序看看。

左边界排序，怎么统计被移除数组的数量？？

上一题的箭的数量就等于没有重叠区域的数量。（例如上题中打4个气球需要三支箭说明有4-3个数重叠了，而没有重叠的元素有三个，相当于本题的要移除出去一个元素）然后本题用数组大小减去箭的数量就是移除元素的数量。

写法一，间接，左区间排序（上题稍改动）

class Solution {
public:static bool cmp(const vector<int>&a,const vector<int>&b){return a[0]<b[0];//按左边界排序} int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.size()==0)return 0;sort(intervals.begin(),intervals.end(),cmp);int count=1;for(int i=1;i<intervals.size();i++){if(intervals[i][0]>=intervals[i-1][1])//如果左边界大于等于上个一维数组的右边界，是不重叠的count++;else intervals[i][1]=min(intervals[i-1][1],intervals[i][1]);//更新当前数组的右边界（其实就是求重叠区间的右边界）}return intervals.size()-count;}
};

写法二，右区间排序

按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。

此时问题就是要求非交叉区间的最大个数。

这里记录非交叉区间的个数还是有技巧的，如图：

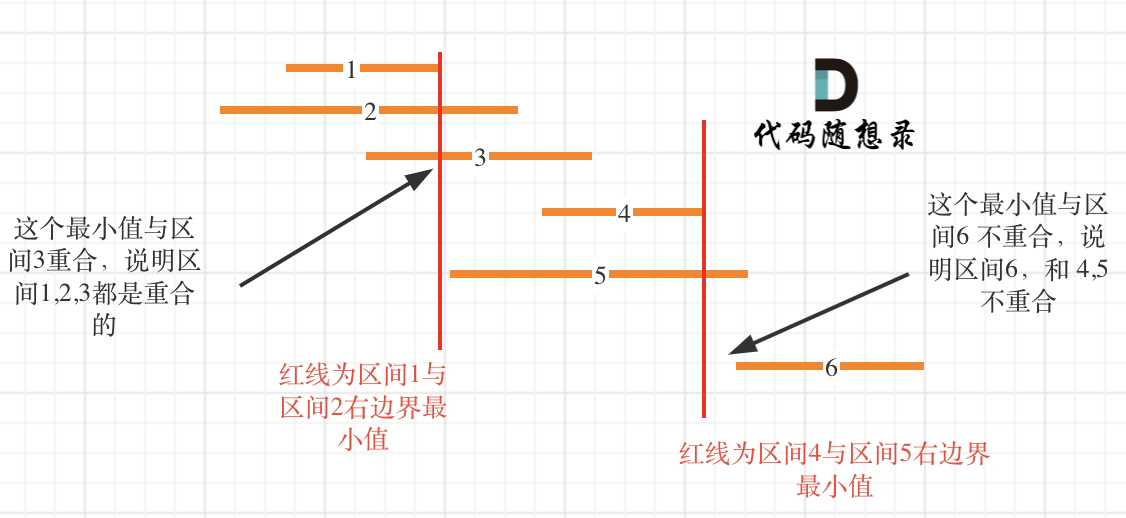
除了右排之外，区别就是这里用了end来记录区间分割点，而且初始值还是第一个数组的右边界。如果遍历过程中找到了重叠的数组的就跳过，直到下一个数组的左边界大于end（初始或更新后的右边界），就更新右边界为当前遍历数组的右边界。于是最后就求出未重叠区间的数量，数组总大小减去该值就是移除数组的数量。

 int end = intervals[0][1]; // 记录区间分割点for (int i = 1; i < intervals.size(); i++) {if (end <= intervals[i][0]) {end = intervals[i][1];count++;}}

如果是使用左边界排序的话可以直接求出移除数组大小。count记录重叠区间数就行。也是在第一种写法上稍加修改就行。 

直接法

class Solution {
public:static bool cmp(const vector<int>&a,const vector<int>&b){return a[0]<b[0];//按左边界排序} int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.size()==0)return 0;sort(intervals.begin(),intervals.end(),cmp);int count=0;//！！！！ 注意这里从0开始，因为是记录重叠区间int end=intervals[0][1];//记录区域分割点，初始值为第一个数组的右边界for(int i=1;i<intervals.size();i++){if(intervals[i][0]>=end)//如果左边界大于等于上个一维数组的右边界，是不重叠的end=intervals[i][1];//更新区域分割点else {count++;end=min(end,intervals[i][1]);//其实就是重叠部分的右边界}}return count;}
};

其实挺简单的。。。。。就是写法上略微差别。个人更喜欢左区间排序。也有精简的（不用end）

763.划分字母区间

题目：763. 划分字母区间 - 力扣（LeetCode）

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。 

示例 2：

输入：s = "eccbbbbdec"
输出：[10]

 

在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

• 统计每一个字符最后出现的位置（后面的遍历会统一更新的）
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

如图：

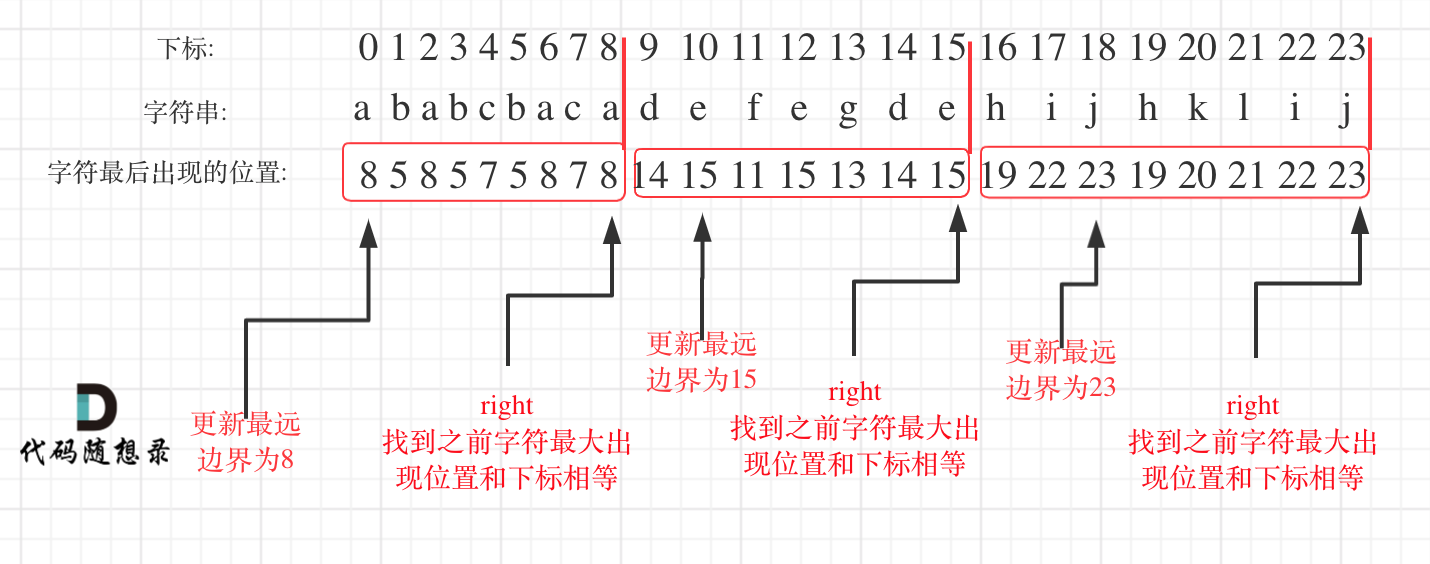
代码

class Solution {
public:vector<int> partitionLabels(string s) {int hash[27]={0};for(int i=0;i<s.size();i++){hash[s[i]-'a']=i; // 统计每一个字符最后出现的位置}vector<int>result;int left=0;int right=0;for(int i=0;i<s.size();i++){right=max(right,hash[s[i]-'a']);//遍历字符串 S。对于每个字符，更新 right 为当前字符的最后出现位置和之前 right 的较大值。if(i==right)//当当前索引 i 等于 right 时，意味着从 left 到 right 的这一部分可以作为一个划分。将这个划分的长度（right - left + 1）添加到 result 中，并更新 left 为下一个字符的索引 i + 1。{result.push_back(right-left+1);left=i+1;}}return result;}
};

不像贪心的贪心。模拟过程。