【LaTex和KaTex】

LaTeX是一种基于ΤΕΧ的排版系统，这种格式可以充分发挥由TeX所提供的强大功能，能在几天，甚至几小时内生成很多具有书籍质量的印刷品。对于生成复杂表格和数学公式，这一点表现得尤为突出。因此它非常适用于生成高印刷质量的科技和数学类文档。

KaTeX，可汗学院出品，号称“最快”的数学公式渲染库。

【一份不太简短的LaTex介绍 PDF】

---

【软件推荐 Mathpix】

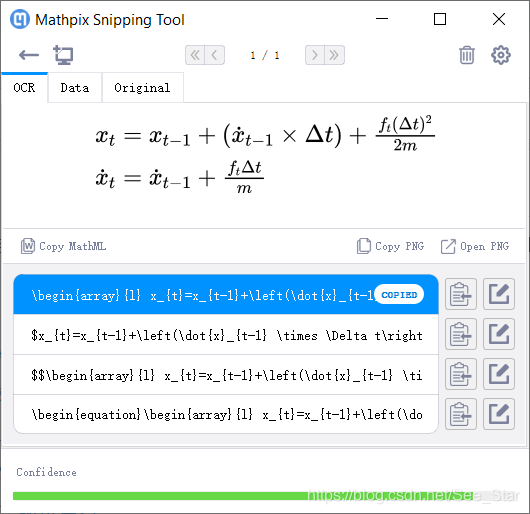
为大家推荐一个软件Mathpix，只需要简单的框选网上、其他文章或是图片中的公式，就能快熟识别成Latex/Markdown格式，然后复制、粘贴到论文里即可。感觉省下很多敲代码的时间。

软件是免费的，注册登录即可使用。【下载地址】

---

一、如何插入公式

1 行中公式
比如，勾股定理$a^2+b^2=c^2$可以写在文字中，并不单独成行。将公式插入在美元符号之间（$...$），像这样$a^2+b^2=c^2$。

2 行间公式
公式也可单独成行，像这样$$a^2+b^2=c^2$$
只要将插入在双美元符号之间（$$...$$），像这样$$a^2+b^2=c^2$$。

二、上下标

公式	效果
$x_2$	$x_2$
$x^2$	$x^2$
$^{22} _2 O ^{-2} _2$	${}_2^{22}{O}_2^{-2}$
$\underset{e}{\overset{f}{_a^bM_c^d}}$	$\underset{e}{\stackrel{f}{{}_a^b{M}_c^d}}$

三、常用运算符

公式	效果
$\times$	$\times$
$\div$	$÷$
$\pm$	$\pm$
$\mp$	$\mp$
$\sum$	$\sum$
$\prod$	$\prod$
$\partial$	$\partial$
$\int$	$\int$
$\displaystyle\int$	$\int$
$\neq$	$\ne$
$\geq$	$\ge$
$\leq$	$\le$
$\approx$	$\approx$
$a \cdot b$	$a\cdot b$
$a \ast b$	$a\ast b$
$\frac{x}{y}$	$\frac{x}{y}$

四、高级运算符

	公式	效果
平均数运算	$\overline{xyz}$	$\overline{xyz}$
开二次方运算	$\sqrt{x}$	$\sqrt{x}$
开方运算	$\sqrt[x]{y}$	$\sqrt[x]{y}$
极限运算	\lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}	${\lim }_{y\to 0}^{x\to \infty }\frac{x}{y}$
极限运算	$\displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$	$\underset{y\to 0}{\overset{x\to \infty }{\lim }}\frac{x}{y}$
求和运算	$\sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$	${\sum }_{y\to 0}^{x\to \infty }\frac{x}{y}$
求和运算	$\displaystyle \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$	$\sum _{y\to 0}^{x\to \infty }\frac{x}{y}$
积分运算	$\int^{\infty}_{0}{xdx}$	${\int }_0^{\infty }xdx$
积分运算	$\displaystyle \int^{\infty}_{0}{xdx}$	${\int }_0^{\infty }xdx$
微分运算	$\frac{\partial x}{\partial y}、\frac{\partial^2x}{\partial y^2}$	$\frac{\partial x}{\partial y}、\frac{{\partial }^{2}x}{\partial y^2}$

五、常用数学符号

	公式	效果
无穷	$\infty$	$\infty$
矢量	$\vec{a}$	$\vec{a}$
一阶导数	$\dot{x}$	$\dot{x}$
二阶导数	$\ddot{x}$	$\ddot{x}$
算数平均值	$\bar{a}$	$\bar{a}$
概率分布	$\hat{a}$	$\hat{a}$
虚数	$\imath$、$\jmath$	$ı$、$ȷ$
省略号	$\ldots$；$\cdots$	$\dots$ ,$\cdots$
省略号	$\vdots$；$\ddots$	$⋮$ ,$\ddots$

六、特殊符号

6.1 箭头

公式	效果
$\uparrow$	$\uparrow$
$\\Uparrow$	$\Uparrow$
$\downarrow$	$\downarrow$
$\Downarrow$	$\Downarrow$
$\leftarrow$	$\leftarrow$
$\Leftarrow$	$\Leftarrow$
$\rightarrow$	$\to$
$\Rightarrow$	$\Rightarrow$
$\updownarrow$	$\updownarrow$
$\Updownarrow$	$\Updownarrow$
$\leftrightarrow$	$\leftrightarrow$
$\Leftrightarrow$	$\iff$

6.2 公式序号

$$y=x+1\text{\hspace{1em}(1,1)}$$

y=x+1\tag{1,1}

七、括号使用

例1：

$$\{\begin{array}{rl}x& =1\\ y& =2+x\end{array}$$

\left\{
\begin{aligned}
x&=1\\
y&=2+x
\end{aligned}
\right.

例2：
$$L(Y,f(x))=\{\begin{array}{l}1,Y!=f(x)\\ 0,Y=f(x)\end{array}$$

L(Y,f(x))=
\begin{cases}
1, Y!=f(x) \\
0, Y = f(x)
\end{cases}

例3：

$$\{\begin{array}{rl}\frac{dr}{d{\omega }^{\prime }}& =\frac{v}{f{\omega }^{\prime }}\\ \frac{dv}{d{\omega }^{\prime }}& =\frac{(F/m)\sin \psi -g/r^2+r_{{\omega }^2}}{f{\omega }^{\prime }}\\ \frac{\mathrm{d}\theta }{\mathrm{d}{\omega }^{\prime }}& =\frac{\omega }{f\omega }\\ \frac{\mathrm{d}\omega }{\mathrm{d}{\omega }^{\prime }}& =-1\\ \frac{\mathrm{d}m}{\mathrm{d}{\omega }^{\prime }}& =-\frac{F}{I_{\mathrm{s}\mathrm{p}}}\cdot \frac{1}{f{\omega }^{\prime }}\end{array}$$

\left\{
\begin{aligned}
\frac{d r}{d \omega^{\prime}}&=\frac{v}{f \omega^{\prime}} \\
\frac{d v}{d \omega^{\prime}}&=\frac{(F / m) \sin \psi-g / r^{2}+r_{\omega^{2}}}{f \omega^{\prime}} \\
\frac{\mathrm{d} \theta}{\mathrm{d} \omega^{\prime}}&=\frac{\omega}{f \omega}\\
\frac{\mathrm{d} \omega}{\mathrm{d} \omega^{\prime}}&=-1 \\
\frac{\mathrm{d} m}{\mathrm{d} \omega^{\prime}}&=-\frac{F}{I_{\mathrm{sp}}} \cdot \frac{1}{f \omega^{\prime}}
\end{aligned}
\right.

八、矩阵

例1：普通矩阵，不带括号
$$\begin{array}{ccccc}a& b& c& d& e\\ f& g& h& i& j\\ k& l& m& n& o\\ p& q& r& s& t\end{array}$$

\begin{matrix} 
a & b & c & d & e\\
f & g & h & i & j\\ 
k & l & m & n & o\\ 
p & q & r & s & t 
\end{matrix}

例2：带中括号的矩阵
$$\left[\begin{array}{ccccc}a& b& c& d& e\\ f& g& h& i& j\\ k& l& m& n& o\\ p& q& r& s& t\end{array}\right]$$

\left[ 
\begin{matrix} 
a & b & c & d & e\\ 
f & g & h & i & j \\ 
k & l & m & n & o \\ 
p & q & r & s & t 
\end{matrix} 
\right]

例3：带大括号的矩阵
$$\left\{\begin{array}{ccccc}a& b& c& d& e\\ f& g& h& i& j\\ k& l& m& n& o\\ p& q& r& s& t\end{array}\right\}$$

\left\{ 
\begin{matrix} 
a & b & c & d & e\\ 
f & g & h & i & j \\ 
k & l & m & n & o \\ 
p & q & r & s & t 
\end{matrix} 
\right\}

例4：矩阵前有参数
$$A=\left\{\begin{array}{ccccc}a& b& c& d& e\\ f& g& h& i& j\\ k& l& m& n& o\\ p& q& r& s& t\end{array}\right\}$$

A= 
\left\{ 
\begin{matrix} 
a & b & c & d & e\\ 
f & g & h & i & j \\ 
k & l & m & n & o \\ 
p & q & r & s & t 
\end{matrix} 
\right\}

例5：矩阵中间有省略号
$$A=\left\{\begin{array}{cccc}a& b& \cdots & e\\ f& g& \cdots & j\\ ⋮& ⋮& \ddots & ⋮\\ p& q& \cdots & t\end{array}\right\}$$

A= 
\left\{ 
\begin{matrix} 
a & b & \cdots & e\\ 
f & g & \cdots & j \\ 
\vdots & \vdots & \ddots & \vdots \\ 
p & q & \cdots & t 
\end{matrix} 
\right\}

\cdots为水平方向的省略号
\vdots为竖直方向的省略号
\ddots为斜线方向的省略号

例6：矩阵中间加根横线
$$A=\left\{\begin{array}{ccccc}a& b& c& d& e\\ f& g& h& i& j\\ k& l& m& n& o\\ p& q& r& s& t\end{array}\right\}$$

A= 
\left\{ 
\begin{array}{cccc|c} 
a & b & c & d & e\\ 
f & g & h & i & j \\ 
k & l & m & n & o \\ 
p & q & r & s & t 
\end{array} 
\right\}

array必须为array
{cccc|c}中的c表示矩阵元素，可以控制|的位置

九、集合运算

	公式	效果
属于	$x \in y$	$x\in y$
不属于	$x \notin y$	$x\notin y$
子集	$x \subset y$	$x\subset y$
子集	$x \supset y$	$x\supset y$
真子集	$x \subseteq y$	$x\subseteq y$
真子集	$x \supseteq y$	$x\supseteq y$
并集	$x \cup y$	$x\cup y$
交集	$x \cap y$	$x\cap y$
属于	$x \setminus y$	$x\setminus y$
同或	$x \bigodot y$	$x⨀y$
同与	$x \bigotimes y$	$x⨂y$
异或	$x \bigoplus y$	$x⨁y$
实数集合	$\mathbb{R}$	$\mathbb{R}$
自然数集合	$\mathbb{Z}$	$\mathbb{Z}$

十、希腊字母

字母名称	公式	效果（大写）	公式	效果（小写）
alpha	$\Alpha$	$\mathrm{A}$	$\alpha$	$\alpha$
beta	$\Beta$	$\mathrm{B}$	$\beta$	$\beta$
gamma	$\Gamma$	$\Gamma$	$\gamma$	$\gamma$
delta	$\Delta$	$\Delta$	$\delta$	$\delta$
epsilon	$\Epsilon$	$\mathrm{E}$	$\epsilon$	$ϵ$
zeta	$\Zeta$	$\mathrm{Z}$	$\zeta$	$\zeta$
eta	$\Eta$	$\mathrm{H}$	$\eta$	$\eta$
theta	$\Theta$	$\Theta$	$\theta$	$\theta$
iota	$\Iota$	$\mathrm{I}$	$\iota$	$\iota$
kappa	$\Kappa$	$\mathrm{K}$	$\kappa$	$\kappa$
lambda	$\Lambda$	$\Lambda$	$\lambda$	$\lambda$
mu	$\Mu$	$\mathrm{M}$	$\mu$	$\mu$
nu	$\Nu$	$\mathrm{N}$	$\nu$	$\nu$
xi	$\Xi$	$\Xi$	$\xi$	$\xi$
omicron	$\Omicron$	$\mathrm{O}$	$\omicron$	$o$
pi	$\Pi$	$\Pi$	$\pi$	$\pi$
rho	$\Rho$	$\mathrm{P}$	$\rho$	$\rho$
sigma	$\Sigma$	$\Sigma$	$\sigma$	$\sigma$
tau	$\Tau$	$\mathrm{T}$	$\tau$	$\tau$
upsilon	$\Upsilon$	${\rm Y}$	$\upsilon$	$\upsilon$
phi	$\Phi$	$\Phi$	$\phi$	$\varphi$
chi	$\Chi$	$\mathrm{X}$	$\chi$	$\chi$
psi	$\Psi$	$\Psi$	$\psi$	$\psi$
omega	$\Omega$	$\Omega$	$\omega$	$\omega$

十一、字符大小

公式	效果
$\tiny x$	$x$
$\scriptsize x$	$x$
$\footnotesize x$	$x$
$\small x$	$x$
$\normalsize x$	$x$
$x$	$x$
$\large x$	$x$
$\Large x$	$x$
$\LARGE x$	$x$
$\huge x$	$x$
$\Huge x$	$x$