-
计算极限 lim n → ∞ 2024 n ( 1 − cos 1 n 2 ) n 3 1 + n 2 − n \mathop {\lim }\limits_{n \to \infty } \frac{{\sqrt[n]{{2024}}\left( {1 - \cos \frac{1}{{{n^2}}}} \right){n^3}}}{{\sqrt {1 + {n^2}} - n}} n→∞lim1+n2−nn2024(1−cosn21)n3
lim n → ∞ 2024 n ( 1 − cos 1 n 2 ) n 3 1 + n 2 − n = lim n → ∞ 1 2 ( 1 n 2 ) 2 n 3 ( 1 + n 2 + n ) 1 lim n → ∞ 2024 n = 1 \begin{align*} \lim_{n \to \infty} \frac{\sqrt [n]{2024} \left( 1 - \cos \frac{1}{n^2} \right) n^3}{\sqrt{1 + n^2} - n} &= \lim_{n \to \infty} \frac{\frac{1}{2} \left( \frac{1}{n^2} \right)^2 n^3 \left( \sqrt{1 + n^2} + n \right)}{1} \lim_{n \to \infty} \sqrt [n]{2024} \\ &= 1 \end{align*} n→∞lim1+n2−nn2024(1−cosn21)n3=n→∞lim121(n21)2n3(1+n2+n)n→∞limn2024=1
-
计算定积分 ∫ 0 π cos 2 x e x d x \int_0^\pi \cos^2 x e^x \, \mathrm{d}x ∫0πcos2xexdx
∫ 0 π cos 2 x e x d x + ∫ 0 π sin 2 x e x d x = ∫ 0 π e x d x = e π − 1 ∫ 0 π cos 2 x e x d x − ∫ 0 π sin 2 x e x d x = ∫ 0 π cos 2 x e x d x = ( k 1 cos 2 x + k 2 sin 2 x ) e x ∣ 0 π \begin{align*} \int_0^\pi \cos^2 x e^x \, \mathrm{d}x + \int_0^\pi \sin^2 x e^x \, \mathrm{d}x &= \int_0^\pi e^x \, \mathrm{d}x \\ &= e^\pi - 1 \\ \int_0^\pi \cos^2 x e^x \, \mathrm{d}x - \int_0^\pi \sin^2 x e^x \, \mathrm{d}x &= \int_0^\pi \cos 2x e^x \, \mathrm{d}x \\ &= \left( k_1 \cos 2x + k_2 \sin 2x \right) e^x \bigg|_0^\pi \end{align*} ∫0πcos2xexdx+∫0πsin2xexdx∫0πcos2xexdx−∫0πsin2xexdx=∫0πexdx=eπ−1=∫0πcos2xexdx=(k1cos2x+k2sin2x)ex 0π
由方程组 k 1 + 2 k 2 = 1 {k_1} + 2{k_2} = 1 k1+2k2=1, k 2 − 2 k 1 = 0 {k_2} - 2{k_1} = 0 k2−2k1=0 可得 k 1 = 1 5 {k_1} = \frac{1}{5} k1=51, k 2 = 2 5 {k_2} = \frac{2}{5} k2=52。
( 1 5 cos 2 x + 2 5 sin 2 x ) e x ∣ 0 π = 1 5 ( e π − 1 ) \begin{align*} \left( \frac{1}{5} \cos 2x + \frac{2}{5} \sin 2x \right) e^x \bigg|_0^\pi &= \frac{1}{5} \left( e^\pi - 1 \right) \end{align*} (51cos2x+52sin2x)ex 0π=51(eπ−1)
故原式为 3 5 ( e π − 1 ) \frac{3}{5} \left( e^\pi - 1 \right) 53(eπ−1)。
-
计算曲线积分
∮ C y 1 + x 2 d x + ( 4 x + ln ( x + 1 + x 2 ) ) d y \oint_C \frac{y}{\sqrt{1 + x^2}} \, \mathrm{d}x + \left( 4x + \ln \left( x + \sqrt{1 + x^2} \right) \right) \, \mathrm{d}y ∮C1+x2ydx+(4x+ln(x+1+x2))dy其中曲线 C C C 为从 A ( 1 , 0 ) A(1,0) A(1,0) 到 B ( − 1 , 0 ) B(-1,0) B(−1,0) 的上半圆周,方向为逆时针。
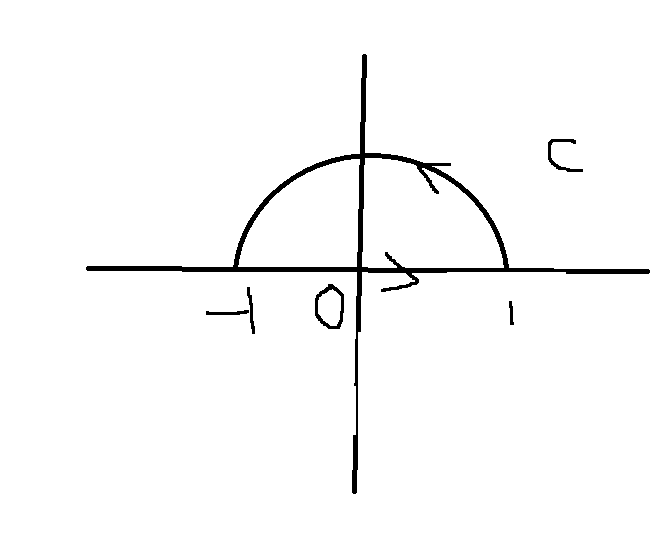
∮ C y 1 + x 2 d x + ln ( x + 1 + x 2 ) d y = ∮ C 4 x d y = ∫ 0 π 4 cos 2 θ d θ = ∫ 0 π 2 ( cos 2 θ + 1 ) d θ = 2 π \begin{align*} \oint_C \frac{y}{\sqrt{1 + x^2}} \, \mathrm{d}x + \ln \left( x + \sqrt{1 + x^2} \right) \, \mathrm{d}y &= \oint_C 4x \, \mathrm{d}y \\ &= \int_0^\pi 4 \cos^2 \theta \, \mathrm{d}\theta \\ &= \int_0^\pi 2 \left( \cos 2\theta + 1 \right) \, \mathrm{d}\theta \\ &= 2\pi \end{align*} ∮C1+x2ydx+ln(x+1+x2)dy=∮C4xdy=∫0π4cos
2024数学分析【南昌大学】
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/457268.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
【Vulnhub靶场】DC-4
DC-4靶场下载地址https://www.five86.com/downloads/DC-4.zip 本机IP:192.168.118.128 靶机IP:192.168.118.0/24 信息收集
扫描主机存活,扫描端口,扫描服务
第一步扫描出主机ip为192.168.118.141
nmap -sP 192.168.118.0/24
nm…
通过rancher2.7管理k8s1.24及1.24以上版本的k8s集群
目录 初始化实验环境
安装Rancher
登录Rancher平台
通过Rancher2.7管理已存在的k8s最新版集群 文档中的YAML文件配置直接复制粘贴可能存在格式错误,故实验中所需要的YAML文件以及本地包均打包至网盘.
链接:https://pan.baidu.com/s/1oYX4eGoBtW_R-7i…
canvas-editor首行缩进
canvas-editor中渲染部分的源码都在Draw.ts里,能找到computeRowList方法中并没有实现首行缩进相关的逻辑,但是实现了element.type ElementType.TAB的缩进,如图: 因此我们可以基于tab进行首行缩进的逻辑编写,在main.ts…
GoogleChrome和Edge浏览器闪屏问题
GoogleChrome和Edge浏览器闪屏问题 文章目录 GoogleChrome和Edge浏览器闪屏问题 买了电脑半年, GoogleChrome和edge浏览器出现了一个令人头疼的问题–闪屏, 就是打开这两个浏览器之后, 就会出现电脑屏幕一闪一闪的, 过一会就看不见了, 跟黑夜里的闪电一样, 遇到这种情况我都会直…
《 C++ 修炼全景指南:十七 》彻底攻克图论!轻松解锁最短路径、生成树与高效图算法
摘要
1、引言
1.1、什么是图?
图(Graph)是计算机科学和离散数学中一种重要的数据结构,用来表示一组对象之间的关系。一个图由顶点(也称为节点,Vertex)和边(Edge)组成。…
【Python爬虫实战】Selenium自动化网页操作入门指南
#1024程序员节|征文# 🌈个人主页:易辰君-CSDN博客 🔥 系列专栏:https://blog.csdn.net/2401_86688088/category_12797772.html 目录
前言
一、准备工作
(一)安装 Selenium 库
࿰…
VMware Workstation Pro 16 搭建 android-x86过程问题罗列
1、搭建完成后,app安装显示软件包解析失败或app打开闪退
测试了android-x86_64-9.0-r2这个版本,发现按照网上部署arm库方法没有成功,最后使用android-x86-7.1-r5版本解决了问题
2、android-x86网络连接不通
虚拟机网络设置选择桥接模式 安…
低代码平台如何通过AI赋能,实现更智能的业务自动化?
引言 随着数字化转型的加速推进,企业在日常运营中面临的业务复杂性与日俱增。如何快速响应市场需求,优化流程,并降低开发成本,成为各行业共同关注的核心问题。低代码平台作为一种能够快速构建应用程序的工具,因其可视化…
Springboot 使用EasyExcel导出Excel文件
Springboot 使用EasyExcel导出Excel文件 Excel导出系列目录:引入依赖创建导出模板类创建图片转化器 逻辑处理controllerservice 导出效果遗留问题 Excel导出系列目录:
【Springboot 使用EasyExcel导出Excel文件】 【Springboot 使用POI导出Excel文件】 …
如何提高游戏的游戏性
改进游戏玩法是一个动态的过程,需要深入了解是什么让玩家保持参与、挑战和兴奋,以获得更多。优秀游戏的核心是平衡——乐趣和难度的无缝结合,让玩家在不感到沮丧的情况下为自己的技能感到奖励。微调这种平衡通常涉及调整难度曲线,…
HTML+JavaScript案例分享: 打造经典俄罗斯方块,详解实现全过程
在本文中,我们将深入探讨如何使用 JavaScript 实现经典的俄罗斯方块游戏。俄罗斯方块是一款广为人知的益智游戏,通过操纵各种形状的方块,使其在游戏区域内排列整齐,以消除完整的行来获得分数。 效果图如下: 一、游戏界面与布局
我们首先使用 HTML 和 CSS 来创建游戏的界面…
力扣283-- 移动零
开始做梦的地方 力扣283 : 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。请注意 ,必须在不复制数组的情况下原地对数组进行操作。 何解?
1,暴力枚举:…
Vue前端开发2.2 数据绑定
文章目录 一、初识数据绑定(一)数据绑定概述(二)数据绑定构成1、定义数据2、输出数据 (三)数据绑定案例演示1、创建单文件组件2、切换页面显示组件 (四)将Vue引入HTML页面中1、概述2…
高效文本编辑与导航:Vim中的三种基本模式及粘滞位的深度解析
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…
sheng的学习笔记-AI基础-正确率/召回率/F1指标/ROC曲线
AI目录:sheng的学习笔记-AI目录-CSDN博客 分类准确度问题
假设有一个癌症预测系统,输入体检信息,可以判断是否有癌症。如果癌症产生的概率只有0.1%,那么系统预测所有人都是健康,即可达到99.9%的准确率。
但显然这样的…
Linux中级(DNS域名解析服务器)
一。产生原因1.IP地址:是互联网上计算机唯一的逻辑地址,通过IP地址实现不同计算机之间的相互通信,每台联网计算机都需要通过IP地址来互相联系和分别,但由于IP地址是由一串容易混淆的数字串构成,人们很难记忆所有计算机…
MySql中的锁的分类
锁的分类 MySQL锁可以按模式分类为:乐观锁与悲观锁。按粒度分可以分为全局锁、表级锁、页级锁、行级锁。按属性可以分为:共享锁、排它锁。按状态分为:意向共享锁、意向排它锁。按算法分为:间隙锁、临键锁、记录锁。 二、全局锁、表…
3-petalinux2018.3 摸索记录 - 命令驱动 _ 交叉编译链
一、命令行控制GPIO
对于ps端设备,在板卡的linux系统中,切换到/sys/class/gpio路径下可以看到目前挂载的gpio设备。
export: 导入用户空间
gpiochip: 系统中gpio寄存器信息
unexport: 移除用户空间 以MIO40和MIO42…
数据结构------手撕链表(一)【不带头单向非循环】
文章目录 链表概念链表的使用LinkedList 的几种遍历方式单链表的模拟实现(不带头)链表面试题 观察ArrayList 顺序表的源码发现,底层是使用数组实现的。由于其底层是一段连续空间,当在ArrayList任意位置插入或者删除元素时…
Java基础(7)图书管理系统
目录
1.前言
2.正文
2.1思路
2.2Book包
2.3people包
2.4operation包
2.5主函数
3.小结 1.前言
哈喽大家好吖,今天来给前面Java基础的学习来一个基础的实战,做一个简单的图书管理系统,这里边综合利用了我们之前学习到的类和对象&…
推荐文章
- CRM中的大客户销售是什么?
- 从底层技术分析如何调教你的ChatGPT?
- # [0628] Task04 DQN 算法及进阶
- #深度学习:从基础到实践
- $.ajax #fm,【图片】95范加尔Ajax的荣光,95Ajax战术在FM的复刻。战术以及思想讨论【fm2017吧】_百度贴吧...
- (Transfer Learning)迁移学习在IMDB上训练情感分析模型
- (动手学习深度学习)第13章 计算机视觉---图像增广与微调
- (二)【Jmeter】专栏实战项目靶场drupal部署
- (开源)2023工训大赛智能垃圾分类项目(可循环播放视频,显示垃圾分类信息,拍照识别,垃圾分类,满载报警,压缩)
- (新东方)背单词,记住这200个词根词缀就够了(我自用)
- .Net Core/.Net6/.Net8 ,启动配置/Program.cs 配置
- .net 项目中配置 Swagger