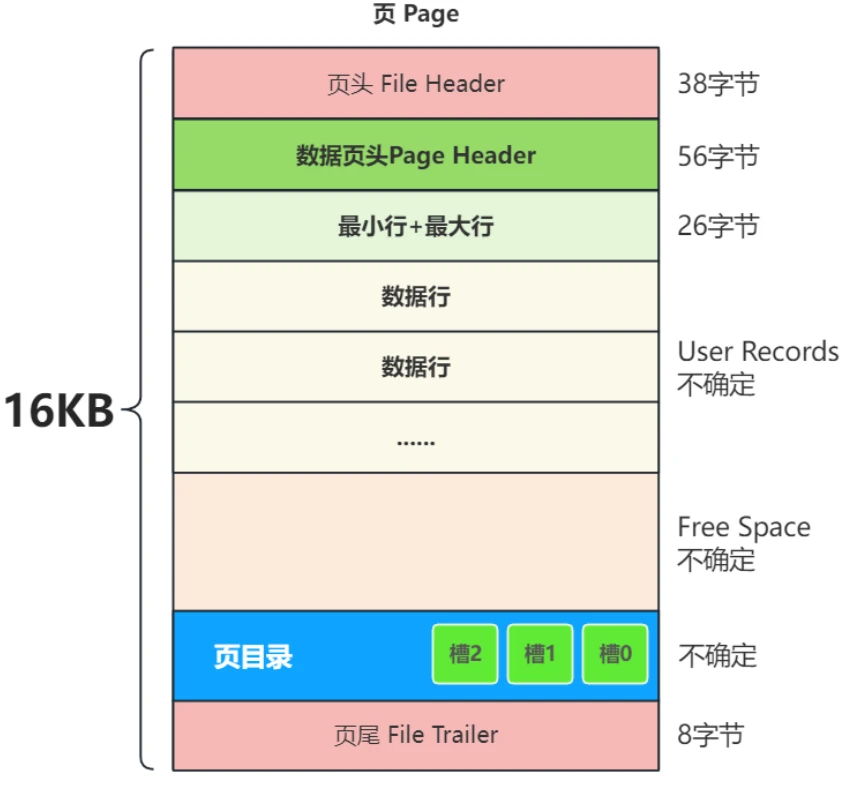
1. 梯度下降缺点：有可能有鞍点（如果不是凸函数的时候），不一定能找到最小值
2. 解决方法：随机梯度下降（选一条数据）和小批量梯度下降（选几条数据
3. 这两个解决方法又会带来新问题，比如收敛过程不稳定、收敛结果持续震荡，解决方案是数据归一化（包括Z-SCORE方法和0-1方法）和学习率调整

归一化算法评价：1.线性模型和聚类模型会受到影响，但树模型不会

1. 会使得模型失去可解释性
2. 归一化后梯度下降速度更快，因为等高线更加均匀

1. SCORE算法更常用（缺点是要算均值方差，慢一些

学习率调整：就是随着梯度下降的过程学习率减小

实际建模过程中，当数据集量较小时：梯度下降+枚举

数据量较大时：小批量梯度下降+学习率调整

24.逻辑回归决策边界是一条直线，而KNN（最近k个邻居决定分类）和决策树则是如下图所示

还有一些模型则是去改变样本空间然后做划分（比如SVM）

注意：逻辑回归中特征值的权重大小并不代表特征的重要性

25、26两节讲了分类模型的评估指标，包括F1-SCORE、ROC-AUC

准确率不好：因为同样把一个样本判定为1，概率为0.8和0.6是不同的，所以一般训练时候用交叉熵做损失函数

为什么不用交叉熵做损失函数：因为损失函数太小会过拟合，要结合其它指标一起判断才好

几个指标：

召回率：1里面识别出多少

准确率：每次识别1有多少正确率

F1-score：两者调和平均

引申：多分类问题怎么办：

分别计算各类的recall然后求平均

ROC曲线：以TPR（即recall）和FPR（负样本中有多少识别为正样本）作为纵横坐标，调整阈值遍历所有样本得到的曲线

另一种理解：TPR看作一类概率的累计结果，FPR看作0类概率累计结果，也就是出现一个1就说明一类概率累计结果上去了

由此我们也可以想出一种例子

这两种其实A效果更好，但ROC是判断不出的，因为都是11010，但交叉熵可以判断出。也就是说ROC只对排序结果敏感，对概率大小无感。

但也不用担心这个问题，一方面，交叉熵损失函数可能导致过拟合，ROC可以消除这个问题；而概率敏感这个问题可以通过手动调整阈值来让它变得概率敏感。

F1-score和ROC对比：前者更偏重对1类样本的判别能力，而ROC是类别对称的，这也提供了评判指标的选择依据。