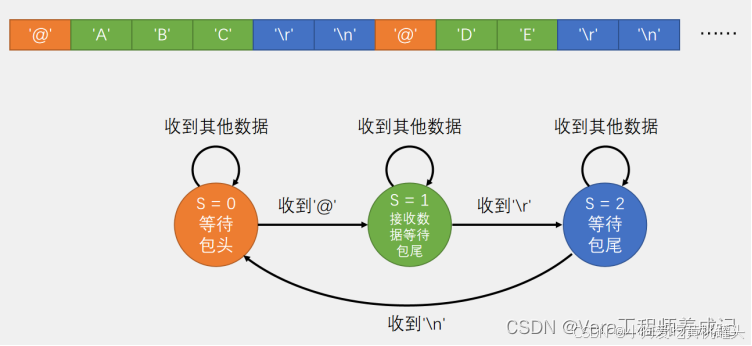
一 几何失真（畸变）的概念

在实际的成像系统中，图像捕捉介质平面和物体平面之间不可避免地存在有一定的转角和倾斜角。转角对图像的影响是产生图像旋转，倾斜角的影响表现为图像发生投影变形。另外一种情况是由于摄像机系统本身的原因导致的镜头畸变。此外，还有由于物体本身平面不平整导致的曲面畸变如柱形畸变等。这些畸变统称为几何畸变。
光学系统、电子扫描系统失真而引起的斜视畸变、投影畸变、枕形、桶形畸变、混合畸变、柱面畸变等，都可能使图像产生几何特性失真，这些系统失真导致的常见的图像几何畸变如图所示：

几何畸变又可分为线性几何畸变和非线性几何畸变。通常情况下，线性几何畸变指缩放、平移、旋转等畸变。而非线性几何畸变是由成像面和物平面的倾斜、物平面本身的弯曲、光学系统的像差造成的畸变，表现为物体与实际的成像各部分比例失衡。
常见几何畸变退化问题的复原大多是基于成像系统，如模拟鱼眼和针孔系统进行摄像机标定，通过确定摄像机畸变参数对所获取图像进行后续校正和复原处理。其优点是一旦确立成像模型，便可以快速有效地根据模型参数对基本图像进行几何变换，从而实现复原。但通常情况下我们面临的图像其成像系统未知且多样化，因此，这种方法不适合于解决一般性无法预知模型的畸变退化。
比如由成像面不平整造成的曲面畸变。因此，另外一种常见的解决方法是多项式变换技术，其实质是利用数值分析的方法求解几何变换方程。其优点是不需要预先知道成像模型，对复杂曲面畸变能够进行校正和复原。缺点是运算量大，不适宜实时性较高系统，对多项式次数和控制点的选取要求严格，发生复原失控的概率很大，不适用于一些只存在投影变换和镜头畸变的图像。这里我们重点介绍基于多项式变换的几何校正方法，其基本流程是先建立几何校正的数学模型，比如针对畸变特点选择一次多项式或者二次多项式作为几何校正的数学模型；其次利用已知条件确定模型参数，通常以标准未畸变影像为参考，由用户在参考影像与畸变影像上选择控制点（同名点），从而解算出多项式系数，即确定出模型参数；最后根据模型对图像进行几何校正。通常由如下两步来完成：
（1）图像空间坐标变换（确定校正后图像中每个像素的空间坐标）；首先建立图像像点坐标（行、列号）和物方（或参考图）对应点坐标间的映射关系，解求映射关系中的未知参数，然后根据映射关系对图像各个像素坐标进行校正；
（2）灰度内插（确定校正影像中每个像素的灰度值）
几何校正的坐标变换
实际工作中常以一幅图像为基准，去校正另一幅几何失真图像。通常设基准图像f(x,y)是利用没畸变或畸变较小的摄像系统获得的，而有较大几何畸变的图像用g(x´,y´)表示，下图是一种畸变情形。

设两幅图像几何畸变的关系能用解析式描述为

通常h1(x，y)和h2(x，y)可用多项式来近似

包含12 个未知数，至少需要6 个已知点来建立关系式，解求未知数。
几何校正方法可分为直接法和间接法两种。
（1） 直接法
利用若干已知点（就是通常所说的控制点）坐标，根据参考图像中像素坐标与校正后影像的像素坐标的对应关系，如下式所示，(x, y)为参考图像坐标，(x’, y’)为(x, y)对应的校正后影像坐标：

通过解求未知参数得到二者的对应关系；然后如上图实线箭头所示，从畸变图像出发，根据上述关系依次计算每个像素的校正坐标，同时把像素灰度值赋予对应像素，这样生成一幅校正图像。
该方法存在的一个问题是图像像素分布是不规则的，会出现像素挤压、疏密不均等现象，不能满足原始未畸变影像的要求，因此最后还需对不规则图像通过灰度内插生成规则的栅格图像。
（2） 间接法
先根据下式


对如图所示的畸变图像的四个角点a、b、c、d 进行坐标变换，获得a´、b´、c´、d´。由此确定校正图像的范围。再按下式

反求像点（x, y）在已知畸变图像上的坐标(x’, y’)。由于计算所得的 (x’, y’)坐标值一般不为整数，不会位于畸变图像像素中心，因而不能直接确定该点的灰度值，而只能在畸变图像上，由该像点周围的像素灰度值通过内插，求出该像素的灰度值，作为(x, y)点的灰度。按上述步骤获得校正图像。由于间接法内插灰度容易，所以一般采用间接法进行几何纠正。

二 灰度内插方法及其特点

常用的像素灰度内插法有最近邻元法、双线性内插法和三次内插法三种。
1．最近邻元法
在待求点的四邻像素中，将距离这点最近的相邻像素灰度赋给该待求点，如下图所示，十字点为计算所得坐标位置，其距离左上角给予红色标记的像素最近，因此，将该红色像素的灰度值赋给纠正后对应的像素。该方法最简单，效果尚佳，但校正后的图像有明显锯齿状，即存在灰度不连续性。

2．双线性内插法
双线性内插法是利用待求点四个邻像素的灰度在两个方向上作线性内插。如图，下面推导待求像素灰度值的计算式。

结合前面两个计算结果，得到上式，校正点像素灰度值为相邻四个像素的线性加权和，因此，称为线性内插该方法要比最近邻元法复杂，计算量大。但没有灰度不连续性的缺点，结果令人满意。它具有低通滤波性质，使高频分量受损，图像轮廓有一定模糊。

3．三次内插法
该方法利用三次多项式S(x)来逼近理论上的最佳插值函数sin(x)/x。其数学表达式为：



红色像素为(x,y)像素坐标邻近原图像坐标(i,j)，以该(i,j)为参考，取(x,y)周围16 个像素，它们的坐标以此为左上角(i-1,j-1),右上角(i-1,j+2)，左下角(i+2,j-1),右下角(i+2,j+2).待求像素(x,y)的灰度值由其周围十六个点的灰度值加权内插得到。可推导出待求像素的灰度计算式如下：f(x,y)=A‧B ‧ C其中

u,v 为内插点距离其最邻近像素f (i,j) 的距离该算法计算量最大，但内插效果最好，精度最高。下图给出了三种不同像素灰度内插方法的效果，可以看出，三次内插法效果最好，最平滑