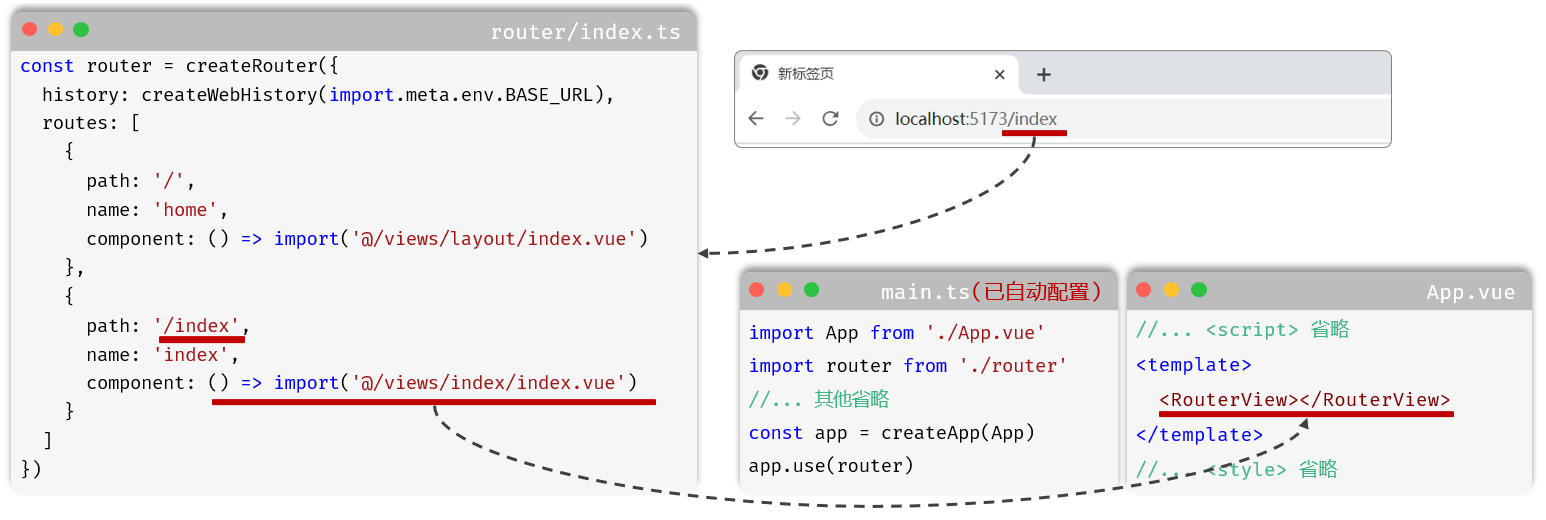
（出这么难是要打坤我嘛）

Minimax

1.构造题？思维题？根据特殊性质可知，一共有两种情况：

[1].只有一种字符，直接输出原字符串即可（10分）。

[2].有多种字符：

(1)存在一种字符出现次数为1:显然把这个字符放在最前面，其他字符排序后接在后面即可。

(2)所有字符出现次数大于等于2:不妨设最小的字符为 a，其出现次数为 cnt。最后的答案为 1。由于要保证字典序最小，我们尽可能多地把 a 放在最前。不难发现最前面最多有连续两个 a。

        如果最前面可以放连续两个 a:考虑除这两个 a 以外的 a，由于这些 a 不能连续出现，所以这些 a 每个后要么接一个非 a 的字符，要么放在字符串尾。所以，字符串最前面可以放连续两个 a，当且仅当 cnt−1≤len−cnt+1 。显然把所有非 a 的字符排序，在相邻两个字符间依次插入 a 直至 a 用完。如果 a 没有用完则一定还剩 1 个 a，放在串最后即可。

        如果最前面不能放连续两个 a:那么，最前面只能放一个 a。在其之后一定会接第二小的字符，不妨设为 b。那么，后面不能再出现形如 ab 这样的串了。若字符种类 ≤2，所有的 a 应放在所有的 b 之后。否则可以在最前面的 b 后接所有的 a，再接一个第三小的字符（设为 c ），然后剩下的字符放置的位置没有限制，直接从小到大排序即可。

2.代码实现：

#include<bits/stdc++.h>
using namespace std;
int t,a[30];
string s;
int main(){cin>>t;while(t--){cin>>s;memset(a,0,sizeof(a));int cnt=0;for(int i=0;i<s.size();i++){if(a[s[i]-'a'+1]==0)cnt++;a[s[i]-'a'+1]++;}if(cnt==1){cout<<s<<endl;continue;}bool flag=0;for(int i=1;i<=26;i++)if(a[i]==1){cout<<(char)(i+'a'-1);a[i]--;for(int i=1;i<=26;i++)for(int j=1;j<=a[i];j++)cout<<(char)(i+'a'-1);cout<<endl;flag=1;break;}if(flag) continue;int x=1;while(a[x]==0)x++;int y=x+1;while(a[y]==0)y++;if(2*a[x]<=s.size()+2){cout<<(char)(x+'a'-1)<<(char)(x+'a'-1);a[x]-=2;for(int i=1;i<=a[x];i++){while(a[y]==0)y++;cout<<(char)(y+'a'-1);cout<<(char)(x+'a'-1);a[y]--;}a[x]=0;for(int i=1;i<=26;i++)for(int j=1;j<=a[i];j++)cout<<(char)(i+'a'-1);cout<<endl;continue;}if(cnt==2){for(int i=1;i<=26;i++)if(a[i]>0){cout<<(char)(i+'a'-1);a[i]--;for(int j=i+1;j<=26;j++)for(int k=1;k<=a[j];k++)cout<<(char)(j+'a'-1);for(int k=1;k<=a[i];k++)cout<<(char)(i+'a'-1);cout<<endl;break;}continue;}cout<<(char)(x+'a'-1)<<(char)(y+'a'-1);a[x]--;a[y]--;for(int i=1;i<=a[x];i++)cout<<(char)(x+'a'-1);a[x]=0;y++;while(a[y]==0)y++;cout<<(char)(y+'a'-1);a[y]--;for(int i=1;i<=26;i++)for(int j=1;j<=a[i];j++)cout<<(char)(i+'a'-1);cout<<endl;}return 0; 
}

Bear and Cavalry

1.打着打着暴力突然想到了匈牙利算法（关于给士兵和奶龙牵线搭桥这回事）

暴力代码（模拟就能发现其实有不少漏洞）：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,q;
long long ans;
struct army{int w,id,vis;
}a[N];
struct kl{int h,id,vis;
}k[N];
bool cmp1(army x,army y){return x.w>y.w;
}
bool cmp2(kl x,kl y){return x.h>y.h;
}
int main(){cin>>n>>q;for(int i=1;i<=n;i++){cin>>a[i].w;a[i].id=i;a[i].vis=0;}for(int i=1;i<=n;i++){cin>>k[i].h;k[i].id=i;k[i].vis=0;}sort(a+1,a+1+n,cmp1);while(q--){int x,y;cin>>x>>y;ans=0;swap(k[x].id,k[y].id);sort(k+1,k+1+n,cmp2);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(a[i].id!=k[j].id&&a[i].vis==0&&k[j].vis==0){ans+=a[i].w*k[j].h;a[i].vis=1;k[i].vis=1;break;}}}for(int i=1;i<=n;i++) k[i].vis=0,a[i].vis=0;cout<<ans<<endl;}return 0;
}

2.设 bani​ 表示 i 不能匹配的马。则有结论：把 w,h 排序后，每个人 i 匹配的马必定在 [i−2,i+2] 中。（证明不会）。考虑一组匹配 (i,i+3)。此时，左下比右下多了三个点，所以至少有三组匹配跨越了 (i,i+3)。红线中可能有一匹马为 bani​，无法交换它和 (i,i+3)；有一个人 j 的 ban 为 i+3，也无法交换它和 (i,i+3)。但这样总会剩下一组可以交换。交换后，逆序对数变少了，显然权值更大。所以不会存在 (i,i+3) 的匹配。(i,i−3) 同理。同时，我们也可以通过交换的过程得到一条性质：如果前 ii 个人和前 ii 匹马匹配完成，那么存在k≤3，使得 [i,i+k] 中的人和马匹配。可以用反证法，得到必然存在一种交换方式。设 fi​ 表示前 i 个人和前 i 匹马匹配完成的最大权值，只从 fi−3​,fi−2​,fi−1​ 转移。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=3e4+10;
const ll inf=1e18;
int n,q,pos[N];
struct node{ll v;int id;
}a[N],b[N];
struct mar{ll A[3][3];
}B;
struct tree{int l,r;mar s;
}tr[N<<2];
inline mar operator*(mar a,mar b){mar c;c.A[0][0]=max(a.A[0][0]+b.A[0][0],max(a.A[0][1]+b.A[1][0],a.A[0][2]+b.A[2][0]));c.A[0][1]=max(a.A[0][0]+b.A[0][1],max(a.A[0][1]+b.A[1][1],a.A[0][2]+b.A[2][1]));c.A[0][2]=max(a.A[0][0]+b.A[0][2],max(a.A[0][1]+b.A[1][2],a.A[0][2]+b.A[2][2]));c.A[1][0]=max(a.A[1][0]+b.A[0][0],max(a.A[1][1]+b.A[1][0],a.A[1][2]+b.A[2][0]));c.A[1][1]=max(a.A[1][0]+b.A[0][1],max(a.A[1][1]+b.A[1][1],a.A[1][2]+b.A[2][1]));c.A[1][2]=max(a.A[1][0]+b.A[0][2],max(a.A[1][1]+b.A[1][2],a.A[1][2]+b.A[2][2]));c.A[2][0]=max(a.A[2][0]+b.A[0][0],max(a.A[2][1]+b.A[1][0],a.A[2][2]+b.A[2][0]));c.A[2][1]=max(a.A[2][0]+b.A[0][1],max(a.A[2][1]+b.A[1][1],a.A[2][2]+b.A[2][1]));c.A[2][2]=max(a.A[2][0]+b.A[0][2],max(a.A[2][1]+b.A[1][2],a.A[2][2]+b.A[2][2]));return c;
}
inline bool cmp(node x,node y){return x.v<y.v;
}
inline ll ask(int t,int x,int y,int z){return a[t].id==b[t-x].id||a[t-1].id==b[t-y].id||a[t-2].id==b[t-z].id?-inf:a[t].v*b[t-x].v+a[t-1].v*b[t-y].v+a[t-2].v*b[t-z].v;
}
inline mar get(int x){mar res=B;res.A[1][0]=res.A[2][1]=0;res.A[0][0]=(a[x].id==b[x].id?-inf:a[x].v*b[x].v);if(x>1) res.A[0][1]=max(a[x].id==b[x].id||a[x-1].id==b[x-1].id?-inf:a[x].v*b[x].v+a[x-1].v*b[x-1].v,a[x].id==b[x-1].id||a[x-1].id==b[x].id?-inf:a[x].v*b[x-1].v+a[x-1].v*b[x].v);if(x>2) res.A[0][2]=max(ask(x,0,1,2),max(ask(x,0,2,1),max(ask(x,1,0,2),max(ask(x,1,2,0),max(ask(x,2,0,1),ask(x,2,1,0))))));return res;
}
inline void pushup(int u){tr[u].s=tr[u<<1|1].s*tr[u<<1].s;
}
inline void build(int u,int l,int r){tr[u]={l,r};if(l==r){tr[u].s=get(l);return ;}int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);
}
inline void mdf(int u,int x){if(x>n) return ;if(tr[u].l==tr[u].r){tr[u].s=get(x);return ;}int mid=tr[u].l+tr[u].r>>1;if(x<=mid) mdf(u<<1,x);else mdf(u<<1|1,x);pushup(u);
}
int main(){for(int i=0;i<3;++i){for(int j=0;j<3;++j){B.A[i][j]=-inf;}}scanf("%d%d",&n,&q);for(int i=1;i<=n;++i){scanf("%lld",&a[i].v);a[i].id=i;}sort(a+1,a+1+n,cmp);for(int i=1;i<=n;++i){scanf("%lld",&b[i].v);b[i].id=i;}sort(b+1,b+1+n,cmp);for(int i=1;i<=n;++i) pos[b[i].id]=i;build(1,1,n);while(q--){int x,y;scanf("%d%d",&x,&y);swap(b[pos[x]].id,b[pos[y]].id);swap(pos[x],pos[y]);mdf(1,pos[x]),mdf(1,pos[x]+1),mdf(1,pos[x]+2);mdf(1,pos[y]),mdf(1,pos[y]+1),mdf(1,pos[y]+2);printf("%lld\n",max(tr[1].s.A[0][0],max(tr[1].s.A[0][1],tr[1].s.A[0][2])));}return 0;
}

Shortest Path 

1.不会正解。（直接输出0有10分）

2.40分：暴力求最短路

#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 150010; 
int h[N], e[N], ne[N], idx;
int w[N];
int dist[N];
bool st[N];
int n, m;
void add(int x, int y, int c){w[idx] = c;e[idx] = y;ne[idx] = h[x]; h[x] = idx++;
}
//堆优化适合稀疏图
/*
1. 一号点的距离初始化为零，其他点初始化成无穷大。
2. 将一号点放入堆中。
3. 不断循环，直到堆空。每一次循环中执行的操作为：弹出堆顶（与朴素版diijkstra找到S外距离最短的点相同，并标记该点的最短路径已经确定）。用该点更新临界点的距离，若更新成功就加入到堆中。
*/
int dijkstra(){memset(dist, 0x3f, sizeof(dist));dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({ 0, 1 }); while(heap.size()){PII k = heap.top();heap.pop();int ver = k.second, distance = k.first;if(st[ver]) continue;st[ver] = true;for(int i = h[ver]; i != -1; i = ne[i]){int j = e[i];if(dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({ dist[j], j });}}}if(dist[n] == 0x3f3f3f3f) return -1;else return dist[n];
}
//求1节点到n节点的最短距离
int main(){memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);while (m--){int x, y, c;scanf("%d%d%d", &x, &y, &c);add(x, y, c);}cout << dijkstra() << endl;return 0;
}

哞了个哞

1.子任务1：爆搜

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N=1e5+5;
const int mod=1e9+7;
int n,k;
int a[N];
ll ans;
map<pii,int> mp;
int cnt;
ll qmi(ll a,int b){ll res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;
}
int mods(ll a,ll b){return a*qmi(b,mod-2)%mod;
}
int jie(int x){int res=1;for(int i=2;i<=n;i++){res=res*i%mod;}return res;
}
int main(){freopen("cxk.out","w",stdout);scanf("%d%d",&n,&k);	for(int i=1;i<=n;i++){a[i]=i;}do{for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){if(a[i]<a[j]){mp[{i,j}]++;ans=(ans+qmi(j,k)-qmi(i,k))%mod;}}}}while(next_permutation(a+1,a+n+1));for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){cout<<i<<" "<<j<<": ";cout<<mp[{i,j}]<<endl;}}cout<<cnt<<endl;printf("%d\n",mods(ans,jie(n)));return 0;
}

2.关于后续：一大堆推式子+拉格朗日插值+快速阶乘(the end...)

All in all

难（虽然有的倒是可以拿部分分）